§ 5. Уравнение состояния идеального газа
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 5. Уравнение состояния идеального газа |
| Напечатано:: | Гость |
| Дата: | Saturday, 1 November 2025, 17:46 |
Выясним, как связаны между собой макроскопические параметры идеального газа, которые характеризуют его равновесное состояние: давление, масса всего газа, объём, предоставленный ему, и температура.
Состояние макроскопической системы полностью определено, если известны её макроскопические параметры — давление , масса
, температура
и объём
. Уравнение, связывающее параметры данного состояния, называют уравнением состояния системы. Изменение параметров состояния системы с течением времени называют процессом.
Если при переходе идеального газа из одного состояния в другое число его молекул остаётся постоянным, т. е. масса и молярная масса газа не изменяются, то из уравнений
и
следует:
,
,
(5.1)
где — постоянная Больцмана;
— параметры начального состояния газа, а
— конечного. Из соотношений (5.1) следует, что
,
или
.
(5.2)
При неизменных массе и молярной массе идеального газа отношение произведения его давления и объёма к абсолютной температуре является величиной постоянной.
Уравнение (5.2) связывает два рассматриваемых состояния идеального газа независимо от того, каким образом газ перешёл из одного состояния в другое.
Уравнение состояния в виде (5.2) впервые вывел в 1834 г. французский физик Бенуа Клапейрон (1799–1864), поэтому его называют уравнением Клапейрона.
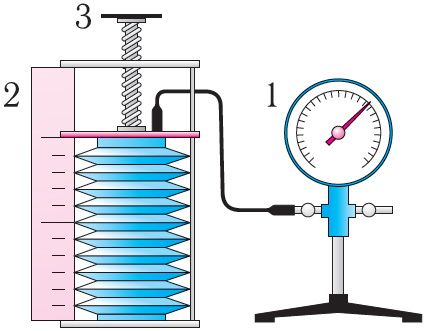
В справедливости уравнения состояния можно убедиться, воспользовавшись установкой, изображённой на рисунке 18. Манометром 1, соединённым с герметичным гофрированным сосудом, регистрируют давление газа внутри сосуда. Объём газа в сосуде можно рассчитать, используя линейку 2. Температура газа в сосуде равна температуре окружающей среды и может быть измерена термометром.
Измерив параметры газа в начальном состоянии, вычисляют отношение
. Затем помещают сосуд в горячую воду. При этом температура газа и его давление изменяются. Вращая винт 3, изменяют вместимость сосуда. Измерив снова давление газа
и температуру
, а также рассчитав предоставленный ему объём
, вычисляют отношение
Как показывают расчёты, уравнение состояния (5.2) выполняется в пределах погрешности эксперимента.
Уравнение состояния (5.2) можно применять для газов при следующих условиях:
1) не очень большие давления (пока собственный объём всех молекул газа пренебрежимо мал по сравнению с предоставленным ему объёмом);
2) не слишком низкие или же высокие температуры (пока абсолютное значение потенциальной энергии межмолекулярного взаимодействия пренебрежимо мало по сравнению с кинетической энергией теплового движения молекул).
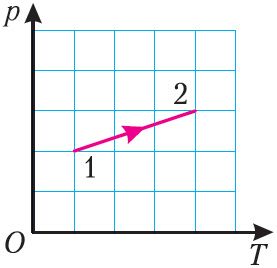
На рисунке 19 представлен график процесса перехода идеального газа данной массы из состояния 1 в состояние 2. Как изменился объём газа в результате этого процесса?
Поскольку число частиц , то из уравнения (5.1) следует:
.
(5.3)
Величину, равную произведению постоянной Больцмана и постоянной Авогадро
, назвали универсальной газовой постоянной
:
.
(5.4)
С учётом выражения (5.4) уравнение (5.3) примет вид:
.
(5.5)
Поскольку количество вещества , то формулу (5.5) можно записать в виде:
.
Уравнение состояния в виде (5.5) впервые получил русский учёный Д. И. Менделеев (1834–1907) в 1874 г., поэтому его называют уравнением Клапейрона–Менделеева.
Отметим, что уравнение Клапейрона–Менделеева связывает между собой макроскопические параметры конкретного состояния идеального газа. Используя уравнение Клапейрона–Менделеева, можно описать различные процессы, происходящие в идеальном газе.
Давление смеси газов. В повседневной жизни часто приходится иметь дело не с газом, состоящим из одинаковых молекул, а со смесью нескольких разнородных газов, не вступающих в химические реакции при рассматриваемых условиях. Например, воздух в комнате является смесью азота (78,08 %), кислорода (20,95 %), инертных газов и водорода (0,94 %), углекислого газа (0,03 %) и в небольших количествах озона, оксида углерода(II), аммиака, метана, оксида серы(IV), а также некоторых других газов (химический состав воздуха приведён в объёмных долях*).
![]()
Вследствие теплового движения частиц каждого газа, входящего в состав газовой смеси, они равномерно распределяются по всему предоставленному смеси объёму. Столкновения частиц обеспечивают в смеси тепловое равновесие.
Каждый газ вносит свой вклад в суммарное давление, производимое газовой смесью, создавая давление, называемое парциальным.
Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.
![]()
Смесь идеальных газов принимают за идеальный газ.
Закон Дальтона. Рассмотрим смесь химически не реагирующих разреженных газов, находящихся в сосуде вместимостью V. Докажем, что давление каждого газа, входящего в состав смеси, не зависит от наличия остальных разреженных газов и результирующее давление определяется суммарным давлением всех компонентов газовой смеси.
Общее число частиц газов в сосуде: , где
— число частиц каждого газа.
Обозначим через парциальные давления каждого газа. Тогда, учитывая соотношение
, получим:
откуда
(5.6)
Формула (5.6) является математическим выражением закона, экспериментально установленного Дальтоном и называемого законом Дальтона: давление смеси химически не реагирующих между собой газов равно сумме парциальных давлений всех газов, образующих смесь.
Из истории физики
Фундаментальные исследования газовых смесей провёл английский учёный Джон Дальтон (1766–1844). Им сформулирован закон независимости парциальных давлений компонентов смеси (1801–1802). В 1802 г. на несколько месяцев раньше французского учёного Жозефа Гей-Люссака (1778–1850) Дальтон установил закон теплового расширения газов, а также ввёл понятие атомного веса.

![]()
1. Что называют уравнением состояния идеального газа?
2. Как связаны параметры идеального газа в уравнении состояния?
3. Какое давление называют парциальным?
![]()
4. Сформулируйте закон Дальтона.
5. Какой воздух тяжелее — сухой или влажный (при одинаковых температуре и давлении)?
* Объёмная доля — процентное отношение содержащихся в единице объёма смеси частиц (атомов или молекул) газа, входящего в состав смеси, к общему количеству частиц в единице объёма смеси. ↑
Пример 1. Баллон с газом, давление которого p1 = 2,84 МПа, находился в неотапливаемом помещении, где температура воздуха t1 = 7 °С. После того как некоторое количество газа было израсходовано, баллон внесли в помещение, где температура воздуха t2 = 27 °С. Определите, какая часть газа была израсходована, если после длительного пребывания баллона в отапливаемом помещении давление газа в нём стало p2 = 1,52 МПа.
p1 = 2,84 МПа = 2,84 · 106 Па
T1 = 280 К, T2 = 300 К
p2 = 1,52 МПа = 1,52 · 106 Па
Решение: Если пренебречь тепловым расширением баллона, то его вместимость не изменяется. Запишем уравнение Клапейрона–Менделеева для начального и конечного состояний газа, считая его идеальным:
,
,
откуда
,
.
Тогда
.
.
Ответ: .
![]()
Пример 2. Определите плотность газовой смеси, состоящей из водорода массой m1 = 8,0 г и кислорода массой m2 = 40 г, если давление и температура смеси р = 1,27 · 105 Па и t = 7 °С соответственно.
m1 = 8,0 г = 8,0 · 10−3 кг
m2 = 40 г = 4,0 · 10−2 кг
p = 1,27 · 105 Па
Т = 280 К
Решение: Плотность газовой смеси
(1)
где m = m1 + m2 — масса смеси, V — объём смеси. Поскольку водород и кислород при низких температурах химически не реагируют, то можно воспользоваться законом Дальтона: р = р1 + р2, где р1 и р2 — парциальные давления водорода и кислорода соответственно.
Их можно определить, воспользовавшись уравнением Клапейрона‒Менделеева:
и
,
где и
— молярные массы водорода и кислорода соответственно. Тогда давление смеси
, а её объём
.
Подставив значения массы m смеси и её объёма V в формулу (1), получим:
Ответ: .
Упражнение 4
1. Определите количество вещества идеального газа, находящегося в сосуде вместимостью V = 480 см3 при нормальных условиях (атмосферное давление р0 = 1,0 · 105 Па, температура t0 = 0,0 °С).
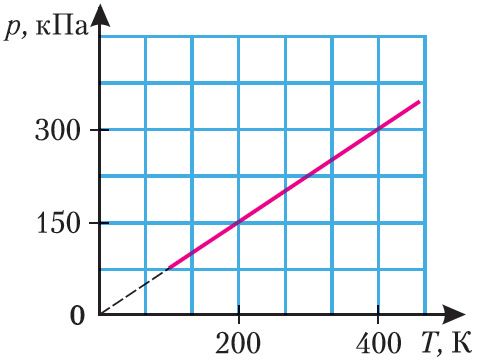
2. На рисунке 20 представлен график зависимости давления водорода, масса которого m = 100 г, от абсолютной температуры. Определите объём, занимаемый газом.
3. Баллон вместимостью V1 = 15 л, содержащий газ, давление которого p1 = 2,0 · 106 Па, соединили с пустым баллоном вместимостью V2 = 5,0 л. Определите давление газа, которое установилось в баллонах, если температура после расширения газа через некоторый промежуток времени оказалась такой же, как и до расширения.
4. Азот, объём которого V1 = 2,9 м3, температура T1 = 293 К и давление p1 = 2,0 · 105 Па, перевели в жидкое состояние. Определите объём, занимаемый жидким азотом, если его плотность .
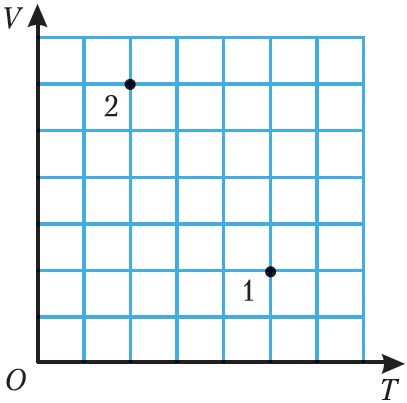
5. На рисунке 21 точки 1 и 2 соответствуют различным состояниям идеального газа определённой массы. Определите, во сколько раз отличаются давления газа в состояниях 1 и 2.
![]()
6. В сосуде вместимостью V = 2,0 л находятся кислород массой m1 = 4,0 г и азот массой m2 = 7,0 г. Определите давление смеси газов, если её абсолютная температура Т = 300 К.
7. В баллоне вместимостью V = 12 л находился идеальный газ, первоначальные давление и температура которого p1 = 1,2 · 105 Па и t1 = 27 °С соответственно. После того как из баллона выпустили часть газа, в нём установилась температура t2 = 17 °С. Определите давление газа, оставшегося в баллоне, если количество вещества выпущенного газа ν1 − ν2 = 0,10 моль.
8. Вакуумированный цилиндрический сосуд вместимостью V = 2 л разделён на две равные части тонкой перегородкой, которая пропускает только молекулы водорода. В одну из частей сосуда впустили водород Н2 и азот N2, массы которых m1 = 4 г и m2 = 14 г соответственно. Определите давление смеси газов, если при достижении теплового равновесия абсолютная температура системы составила Т = 320 К.