§ 5. Уравнение состояния идеального газа: Уравнение состояния идеального газа

§ 5. Уравнение состояния идеального газа

Выясним, как связаны между собой макроскопические параметры идеального газа, которые характеризуют его равновесное состояние: давление, масса всего газа, объём, предоставленный ему, и температура.

Состояние макроскопической системы полностью определено, если известны её макроскопические параметры — давление $p$ , масса $m$ , температура $T$ и объём $V$ . Уравнение, связывающее параметры данного состояния, называют уравнением состояния системы. Изменение параметров состояния системы с течением времени называют процессом.

Если при переходе идеального газа из одного состояния в другое число его молекул $N space equals space m over M N subscript straight A$ остаётся постоянным, т. е. масса и молярная масса газа не изменяются, то из уравнений $p space equals space n k T$ и $n space equals space N over V$ следует:

$p subscript 1 V subscript 1 space equals space N k T subscript 1$ , $p subscript 2 V subscript 2 space equals space N k T subscript 2$ ,

(5.1)

где $k$ — постоянная Больцмана; $p subscript 1 comma space V subscript 1 comma space T subscript 1$ — параметры начального состояния газа, а $p subscript 2 comma space V subscript 2 comma space T subscript 2$ — конечного. Из соотношений (5.1) следует, что

$fraction numerator p subscript 1 V subscript 1 over denominator T subscript 1 end fraction space equals space fraction numerator p subscript 2 V subscript 2 over denominator T subscript 2 end fraction$ ,

или

$fraction numerator p V over denominator T end fraction space equals space const$ .

(5.2)

При неизменных массе и молярной массе идеального газа отношение произведения его давления и объёма к абсолютной температуре является величиной постоянной.

Уравнение (5.2) связывает два рассматриваемых состояния идеального газа независимо от того, каким образом газ перешёл из одного состояния в другое.

Уравнение состояния в виде (5.2) впервые вывел в 1834 г. французский физик Бенуа Клапейрон (1799–1864), поэтому его называют уравнением Клапейрона.

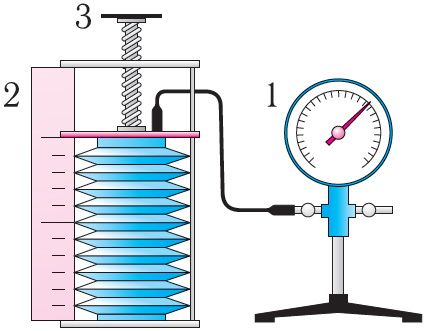
В справедливости уравнения состояния можно убедиться, воспользовавшись установкой, изображённой на рисунке 18. Манометром 1, соединённым с герметичным гофрированным сосудом, регистрируют давление газа внутри сосуда. Объём газа в сосуде можно рассчитать, используя линейку 2. Температура газа в сосуде равна температуре окружающей среды и может быть измерена термометром.

Измерив параметры газа $p subscript 1 comma space V subscript 1 comma space T subscript 1$ в начальном состоянии, вычисляют отношение $fraction numerator p subscript 1 V subscript 1 over denominator T subscript 1 end fraction$ . Затем помещают сосуд в горячую воду. При этом температура газа и его давление изменяются. Вращая винт 3, изменяют вместимость сосуда. Измерив снова давление газа $p subscript 2$ и температуру $T subscript 2$ , а также рассчитав предоставленный ему объём $V subscript 2$ , вычисляют отношение $fraction numerator p subscript 2 V subscript 2 over denominator T subscript 2 end fraction.$ Как показывают расчёты, уравнение состояния (5.2) выполняется в пределах погрешности эксперимента.

Уравнение состояния (5.2) можно применять для газов при следующих условиях:

1) не очень большие давления (пока собственный объём всех молекул газа пренебрежимо мал по сравнению с предоставленным ему объёмом);

2) не слишком низкие или же высокие температуры (пока абсолютное значение потенциальной энергии межмолекулярного взаимодействия пренебрежимо мало по сравнению с кинетической энергией теплового движения молекул).

От теории к практике

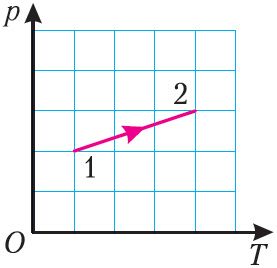
На рисунке 19 представлен график процесса перехода идеального газа данной массы из состояния 1 в состояние 2. Как изменился объём газа в результате этого процесса?

Поскольку число частиц $N space equals space m over M N subscript straight A$ , то из уравнения (5.1) следует:

$p V space equals space k N subscript straight A m over M T$ .

(5.3)

Величину, равную произведению постоянной Больцмана $k$ и постоянной Авогадро $N subscript straight A$ , назвали универсальной газовой постоянной $R$ :

$R space equals space k N subscript straight A space equals space 1 comma 38 times 10 to the power of negative 23 end exponent space Дж over straight К times 6 comma 02 times 10 to the power of 23 space 1 over моль space equals space 8 comma 31 space fraction numerator Дж over denominator моль times straight К end fraction$ .

(5.4)

С учётом выражения (5.4) уравнение (5.3) примет вид:

$p V space equals space m over M R T$ .

(5.5)

Поскольку количество вещества $v space equals space m over M$ , то формулу (5.5) можно записать в виде:

$p V space equals space v R T$ .

Уравнение состояния в виде (5.5) впервые получил русский учёный Д. И. Менделеев (1834–1907) в 1874 г., поэтому его называют уравнением Клапейрона–Менделеева.

Отметим, что уравнение Клапейрона–Менделеева связывает между собой макроскопические параметры конкретного состояния идеального газа. Используя уравнение Клапейрона–Менделеева, можно описать различные процессы, происходящие в идеальном газе.