§ 4. Тепловое равновесие. Температура - мера средней кинетической энергии теплового движения частиц вещества
![]()
Температура и средняя кинетическая энергия поступательного движения молекул газа. Значение температуры при измерении степени нагретости тела определяют по температурному изменению удобного для измерений физического свойства вещества. Примеры термометрических свойств: давление газа, электрическое сопротивление проводника или полупроводника, тепловое расширение жидкости или твёрдого тела. Определение температуры должно основываться на такой физической величине, которая характеризует состояние тел и является одинаковой для любых тел, находящихся в состоянии теплового равновесия. Необходимым свойством обладает средняя кинетическая энергия теплового движения частиц вещества. Тепловое движение частиц вещества существенно изменяется при изменении его агрегатного состояния. Максимально простым оно оказывается у одноатомного газа, атомы которого совершают только поступательное движение.
Возьмём несколько сосудов разной вместимости, снабжённых манометрами для измерения давления (рис. 16). Заполнив их различными газами, например аргоном, неоном и гелием, поместим сначала в сосуд с тающим льдом (t0 = 0 °С), а затем будем изменять температуру содержимого сосуда, пока она не станет равной температуре кипения воды (t = 100 °С).
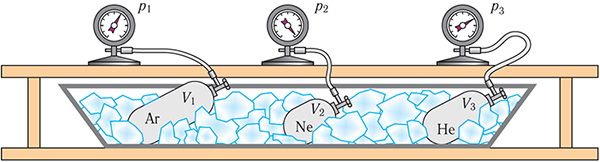
Давления газов в сосудах могут отличаться. Массы газов можно определить взвешиванием откачанных и заполненных сосудов. Зная массу газа и его молярную массу
, по формуле
можно вычислить число частиц и, следовательно, определить их концентрацию
в каждом из сосудов.
Опытным путём установлено, что в состоянии теплового равновесия, несмотря на различные значения давления и концентрации
частиц, отношение давления к концентрации
во всех сосудах оказалось практически одинаковым:
. Это отношение для разреженных газов (удовлетворяющих требованиям модели «идеальный газ») зависит только от степени нагретости тела и характеризует температуру газов в энергетических единицах (в СИ измеряют в джоулях). Единица измерения температуры джоуль неудобна. Например, температура кипения воды, выраженная в джоулях:
Первоначальная термометрия основана на шкале идеального газа, устанавливаемой с помощью газового термометра, для которого зависимость давления от температуры принимают линейной:
(4.1)
где k — коэффициент пропорциональности.
Если при нуле термометрической шкалы термометрическая величина (давление газа) обращается в нуль, то такую шкалу называют абсолютной шкалой, а температуру, отсчитываемую по такой шкале, — абсолютной температурой: p = nkТ. Температура, равная нулю в такой шкале, — температура, при которой давление идеального газа было бы равно нулю. Но это не означает, что идеальный газ можно настолько охладить, что его давление станет равным нулю.
Шкалу, совершенно не зависящую от физических свойств каких бы то ни было веществ, которую можно считать абсолютной и универсальной, предложил в 1848 г. выдающийся английский физик Уильям Томсон (1824–1907), удостоенный за работы в области физики в 1892 г. титула лорда Кельвина. Поэтому эту шкалу обычно называют шкалой Кельвина.
Нулевая точка по шкале Кельвина соответствует самой низкой теоретически возможной температуре (абсолютный нуль температуры). Температура тающего льда по этой шкале T0 = 273,15 К. Связь между температурами по шкале Цельсия (t) и по шкале Кельвина (T) имеет вид: T = t + 273,15.
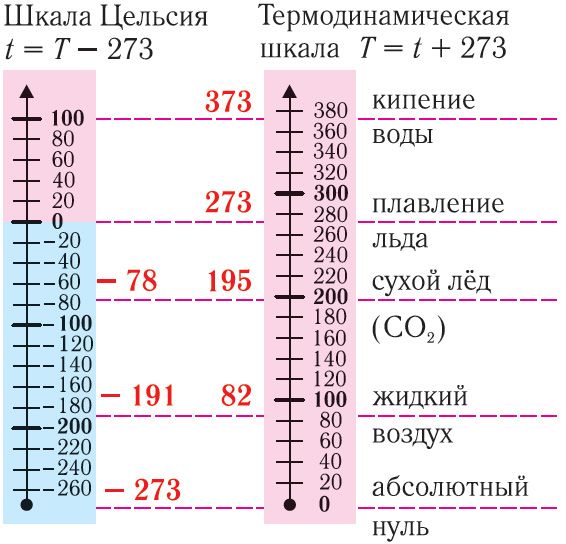
Единица температуры по абсолютной шкале один кельвин (1 К) является основной единицей температуры в СИ и совпадает с одним градусом (1 °С) по шкале Цельсия. Поэтому разность температур по шкале Кельвина и по шкале Цельсия одинакова, т. е. ΔT = Δt (рис. 17).
Выразите по шкале Кельвина температуру тела здорового человека.
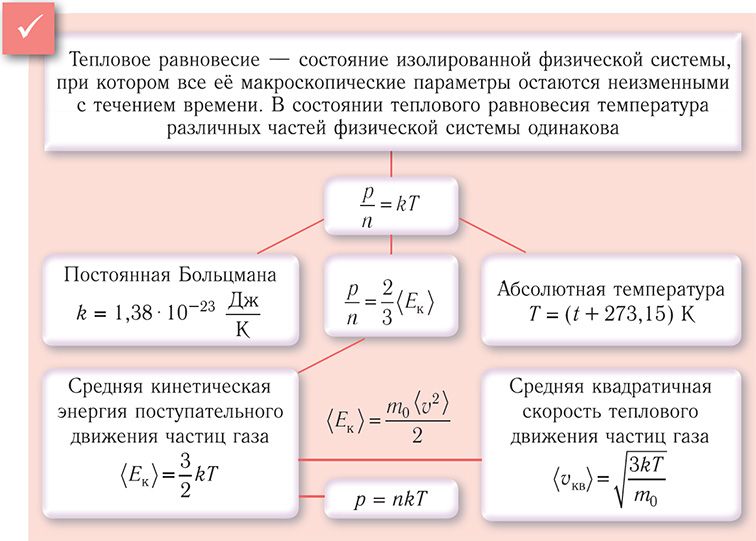
Из основного уравнения молекулярно-кинетической теории идеального газа (3.2) следует: . Таким образом, учитывая выражение (4.1), можно записать:
или
.
(4.2)
Соотношение (4.2) устанавливает связь между абсолютной температурой идеального газа и средней кинетической энергией
поступательного движения его частиц. Таким образом, из формулы (4.2) следует, что средняя кинетическая энергия поступательного движения частиц идеального газа пропорциональна его абсолютной температуре.
Средняя кинетическая энергия поступательного движения молекул газов, находящихся в состоянии теплового равновесия, одинакова для разных газов и не зависит от массы молекулы газа.
Этот вывод, основанный на экспериментах с разреженными газами, справедлив для жидкостей и твёрдых тел.
Уравнение (4.2) можно записать следующим образом: , откуда
.
С учётом формулы (4.1) основное уравнение молекулярно-кинетической теории идеального газа может быть записано в виде:
(4.3)
Из уравнения (4.3) следует, что при одинаковых значениях абсолютной температуры и концентрации
частиц давление любых газов одинаково, независимо от того, из каких частиц они состоят.
1. В состав воздуха у земной поверхности в небольшом количестве входят инертные газы: неон и гелий
. Какова средняя кинетическая энергия теплового движения частиц этих газов при нормальных условиях:
,
? Какие данные из условия можно исключить?
2. Совпадают ли средние квадратичные скорости молекул кислорода и азота в воздухе?
1. Какая величина характеризует состояние теплового равновесия?
2. Можно ли обычным жидкостным термометром измерить температуру капли воды?
3. Как зависит средняя кинетическая энергия поступательного движения молекул идеального газа от температуры?
4. При нагревании газа в баллоне средняя квадратичная скорость молекул увеличилась в два раза. как изменилось давление газа?
5. Что представляет собой абсолютная шкала температур? Что принято за единицу абсолютной температуры в СИ? Каково соотношение между температурами по шкале Цельсия и шкале Кельвина?
6. Как связано давление идеального газа с его абсолютной температурой и концентрацией молекул?