§ 4. Тепловое равновесие. Температура - мера средней кинетической энергии теплового движения частиц вещества
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 4. Тепловое равновесие. Температура - мера средней кинетической энергии теплового движения частиц вещества |
| Напечатано:: | Гость |
| Дата: | Воскресенье, 24 Август 2025, 22:20 |
В повседневной жизни под температурой мы понимаем степень нагретости тела (холодное, тёплое, горячее). Такой подход является довольно субъективным, он зависит не только от состояния рассматриваемого тела, но и от наших ощущений. Чтобы избежать субъективной неопределённости, необходимо установить способ измерения температуры.
Тепловое равновесие. Если привести в соприкосновение два тела, то молекулы этих тел, взаимодействуя между собой, будут обмениваться энергией. При этом молекулы с большей кинетической энергией передают часть энергии молекулам с меньшей кинетической энергией. В результате средняя кинетическая энергия теплового движения молекул одного тела увеличивается, а другого — уменьшается. Отдающее энергию тело называют более нагретым, а тело, к которому энергия переходит, — менее нагретым. Как показывает опыт, такой переход энергии продолжается до тех пор, пока не установится некоторое состояние, в котором тела могут находиться сколь угодно долго. В этом состоянии степень нагретости тел становится и остаётся одинаковой, следовательно, у тел одинаковая температура. Это учитывают при измерении температуры тела. Термометр приводят в соприкосновение с телом, но отсчёт его показаний выполняют не сразу, а через некоторый промежуток времени. Это необходимо для того, чтобы между термометром и телом установилось тепловое равновесие.
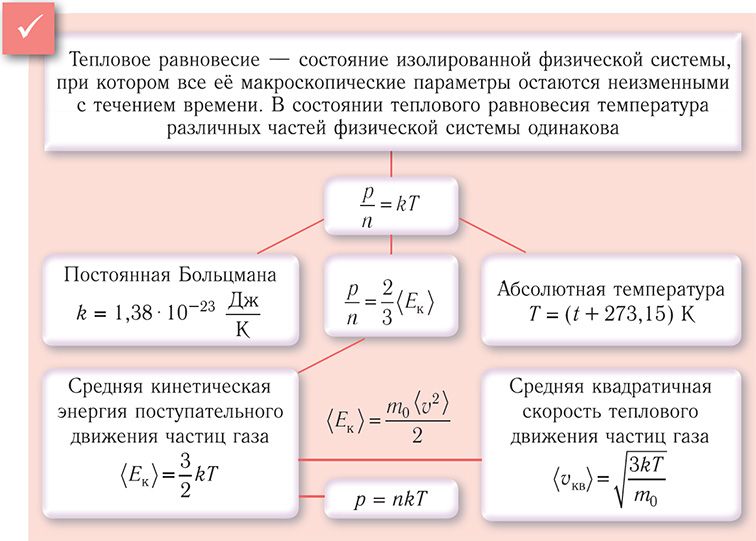
Тепловое равновесие — состояние изолированной физической системы, при котором все её макроскопические параметры остаются неизменными с течением времени.
Под изолированной, или замкнутой, системой понимают систему тел, которая не обменивается энергией с окружающими телами.
Отметим, что у тел, входящих в физическую систему, находящуюся в состоянии теплового равновесия, могут быть различные значения плотности, концентрации, давления и объёма. Однако температура всех тел, входящих в такую систему, всегда одинакова.
1. Температура воды в стакане t = 18 °С. Чему равна температура термометра, погружённого в воду?
2. Погружённый в стакан с водой лабораторный термометр вынули и поднесли к настольной лампе, чтобы лучше рассмотреть его показания. Корректно ли определена температура воды?
Интересно знать
Понятия «градус» и «температура» появились задолго до изобретения термометра. Знаменитый древнеримский врач Гален (II в.) считал, что все лекарства следует различать по «градусам» (от лат. gradus — ступень) теплоты, холода, сухости и влажности. Гален учил, что одни лекарства оказывают охлаждающее действие, а другие — согревающее. При необходимости следовало смешивать лекарства, чтобы умерить излишнее тепло влажностью, а холод — сухостью. От латинского слова temperature (смешение) возник термин «температура».
![]()
Температура и средняя кинетическая энергия поступательного движения молекул газа. Значение температуры при измерении степени нагретости тела определяют по температурному изменению удобного для измерений физического свойства вещества. Примеры термометрических свойств: давление газа, электрическое сопротивление проводника или полупроводника, тепловое расширение жидкости или твёрдого тела. Определение температуры должно основываться на такой физической величине, которая характеризует состояние тел и является одинаковой для любых тел, находящихся в состоянии теплового равновесия. Необходимым свойством обладает средняя кинетическая энергия теплового движения частиц вещества. Тепловое движение частиц вещества существенно изменяется при изменении его агрегатного состояния. Максимально простым оно оказывается у одноатомного газа, атомы которого совершают только поступательное движение.
Возьмём несколько сосудов разной вместимости, снабжённых манометрами для измерения давления (рис. 16). Заполнив их различными газами, например аргоном, неоном и гелием, поместим сначала в сосуд с тающим льдом (t0 = 0 °С), а затем будем изменять температуру содержимого сосуда, пока она не станет равной температуре кипения воды (t = 100 °С).
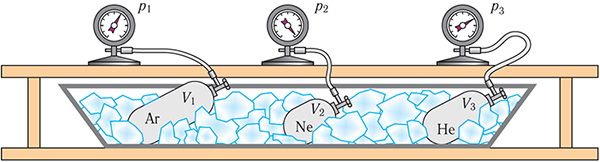
Давления газов в сосудах могут отличаться. Массы газов можно определить взвешиванием откачанных и заполненных сосудов. Зная массу газа и его молярную массу
, по формуле
можно вычислить число частиц и, следовательно, определить их концентрацию
в каждом из сосудов.
Опытным путём установлено, что в состоянии теплового равновесия, несмотря на различные значения давления и концентрации
частиц, отношение давления к концентрации
во всех сосудах оказалось практически одинаковым:
. Это отношение для разреженных газов (удовлетворяющих требованиям модели «идеальный газ») зависит только от степени нагретости тела и характеризует температуру газов в энергетических единицах (в СИ измеряют в джоулях). Единица измерения температуры джоуль неудобна. Например, температура кипения воды, выраженная в джоулях:
Первоначальная термометрия основана на шкале идеального газа, устанавливаемой с помощью газового термометра, для которого зависимость давления от температуры принимают линейной:
(4.1)
где k — коэффициент пропорциональности.
Если при нуле термометрической шкалы термометрическая величина (давление газа) обращается в нуль, то такую шкалу называют абсолютной шкалой, а температуру, отсчитываемую по такой шкале, — абсолютной температурой: p = nkТ. Температура, равная нулю в такой шкале, — температура, при которой давление идеального газа было бы равно нулю. Но это не означает, что идеальный газ можно настолько охладить, что его давление станет равным нулю.
Шкалу, совершенно не зависящую от физических свойств каких бы то ни было веществ, которую можно считать абсолютной и универсальной, предложил в 1848 г. выдающийся английский физик Уильям Томсон (1824–1907), удостоенный за работы в области физики в 1892 г. титула лорда Кельвина. Поэтому эту шкалу обычно называют шкалой Кельвина.
Нулевая точка по шкале Кельвина соответствует самой низкой теоретически возможной температуре (абсолютный нуль температуры). Температура тающего льда по этой шкале T0 = 273,15 К. Связь между температурами по шкале Цельсия (t) и по шкале Кельвина (T) имеет вид: T = t + 273,15.
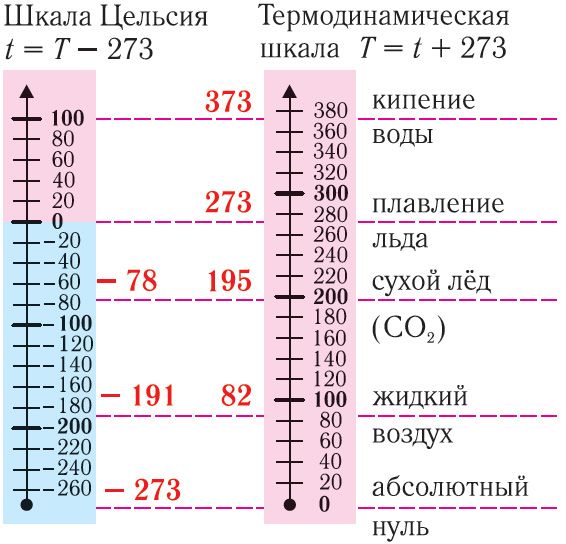
Единица температуры по абсолютной шкале один кельвин (1 К) является основной единицей температуры в СИ и совпадает с одним градусом (1 °С) по шкале Цельсия. Поэтому разность температур по шкале Кельвина и по шкале Цельсия одинакова, т. е. ΔT = Δt (рис. 17).
Выразите по шкале Кельвина температуру тела здорового человека.
Из основного уравнения молекулярно-кинетической теории идеального газа (3.2) следует: . Таким образом, учитывая выражение (4.1), можно записать:
или
.
(4.2)
Соотношение (4.2) устанавливает связь между абсолютной температурой идеального газа и средней кинетической энергией
поступательного движения его частиц. Таким образом, из формулы (4.2) следует, что средняя кинетическая энергия поступательного движения частиц идеального газа пропорциональна его абсолютной температуре.
Средняя кинетическая энергия поступательного движения молекул газов, находящихся в состоянии теплового равновесия, одинакова для разных газов и не зависит от массы молекулы газа.
Этот вывод, основанный на экспериментах с разреженными газами, справедлив для жидкостей и твёрдых тел.
Уравнение (4.2) можно записать следующим образом: , откуда
.
С учётом формулы (4.1) основное уравнение молекулярно-кинетической теории идеального газа может быть записано в виде:
(4.3)
Из уравнения (4.3) следует, что при одинаковых значениях абсолютной температуры и концентрации
частиц давление любых газов одинаково, независимо от того, из каких частиц они состоят.
1. В состав воздуха у земной поверхности в небольшом количестве входят инертные газы: неон и гелий
. Какова средняя кинетическая энергия теплового движения частиц этих газов при нормальных условиях:
,
? Какие данные из условия можно исключить?
2. Совпадают ли средние квадратичные скорости молекул кислорода и азота в воздухе?
1. Какая величина характеризует состояние теплового равновесия?
2. Можно ли обычным жидкостным термометром измерить температуру капли воды?
3. Как зависит средняя кинетическая энергия поступательного движения молекул идеального газа от температуры?
4. При нагревании газа в баллоне средняя квадратичная скорость молекул увеличилась в два раза. как изменилось давление газа?
5. Что представляет собой абсолютная шкала температур? Что принято за единицу абсолютной температуры в СИ? Каково соотношение между температурами по шкале Цельсия и шкале Кельвина?
6. Как связано давление идеального газа с его абсолютной температурой и концентрацией молекул?
В одном из углов комнаты разбрызгайте духи или одеколон. Через некоторый промежуток времени запах распространится по всей комнате. Используя часы с секундной стрелкой, определите среднюю скорость распространения молекул духов (одеколона). Как согласовать полученный результат с достаточно большим значением средней квадратичной скорости поступательного движения молекул газов?
Пример 1. Сравните средние квадратичные скорости атомов гелия и молекул кислорода, если газы находятся в состоянии теплового равновесия.
Решение: Средняя квадратичная скорость теплового движения частиц газа . Поскольку масса одной молекулы вещества
, то
. Так как газы находятся в состоянии теплового равновесия, т. е.
, то средние квадратичные скорости атомов гелия
,
молекул кислорода — .
Тогда:
Ответ: в состоянии теплового равновесия средняя квадратичная скорость атомов гелия в 2,8 раза больше средней квадратичной скорости молекул кислорода.
Пример 2. В баллоне вместимостью V = 14 л находился газ, абсолютная температура которого T = 290 К. Расходуя газ, из баллона выпустили N = 1,0 · 1022 молекул. Определите, на сколько уменьшилось давление газа в баллоне, если через некоторый промежуток времени его температура увеличилась до первоначального значения.
V = 14 л = 1,4 · 10–2 м3
T = 290 К
N = 1,0 · 1022
Решение: Начальное давление газа
.
После того как израсходовали часть газа, а его температура увеличилась до первоначального значения , давление газа стало
.
Тогда убыль давления газа:
.
.
Ответ: .
Упражнение 3
1. Температура куска льда по шкале Цельсия t = –53,0 °С. Чему равна его температура по шкале Кельвина?
2. Температура газа по абсолютной шкале: а) T = 473 К; б) T = 120 К. Чему равна температура газа по шкале Цельсия в каждом случае?
3. Определите среднюю кинетическую энергию поступательного движения частиц идеального газа, температура которого t = 20 °С.
4. Определите число молекул идеального газа, находящегося в сосуде вместимостью V = 1,4 л, если температура газа t = 27 °С, а давление p = 3,0 кПа.
5. Водород, абсолютная температура которого T = 290 К, а масса m = 2,0 кг, находится в сосуде вместимостью V = 2,0 м3. Определите давление водорода.
6. Температура воздуха, находящегося в сосуде, t1 = 24,0 °С. На сколько градусов увеличилась температура воздуха, если средняя кинетическая энергия поступательного движения его молекул увеличилась в α = 2,00 раза?
7. Определите плотность азота, давление которого p = 1,1 · 105 Па и абсолютная температура T = 298 К.
![]()
8. Средняя квадратичная скорость молекул идеального газа, находящегося в герметично закрытом сосуде, увеличилась на α = 20 %. Определите, на сколько процентов изменится давление газа.