§ 30. Моделирование в задачах вычисления координат замечательных точек треугольника
30.15. Создание документальной математической модели (этап 3а)
|
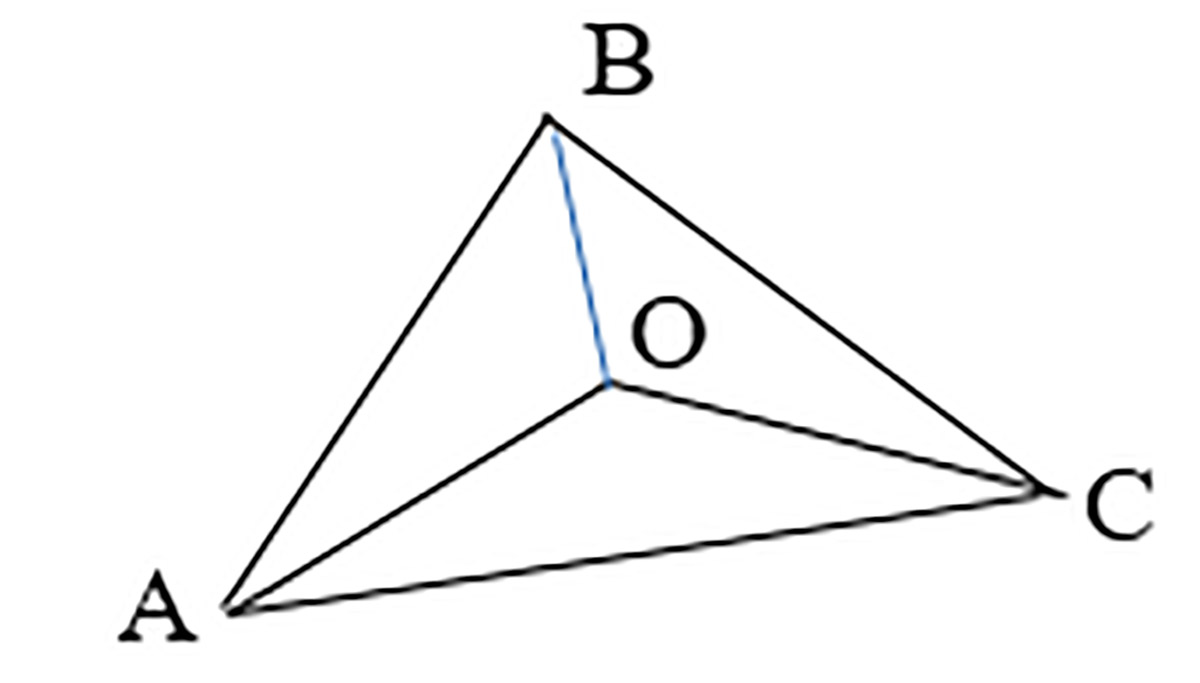
Сохраним обозначения задачи 1 для координат вершин: A(x1; y1), B(x2; y2), C(x3; y3), а обозначение O (латинское) с неизвестными координатами x и y будем использовать для центра вписанной окружности. Расстояние от центра вписанной окружности до одной стороны треугольника равно расстоянию от этого центра до другой стороны и равно радиусу вписанной окружности. Это свойство послужит основанием для создания системы уравнений. Для нахождения расстояния от точки до отрезка на координатной плоскости есть формула (пример 30.23). Поскольку все три высоты равны между собой для центра вписанной окружности, приравниваем пары высот и получаем систему двух уравнений относительно двух неизвестных, решение которой является решением задачи 3.
|
Пример 30.23. Соединим отрезками центр вписанной окружности O и вершины треугольника. Расстояние от точки O до стороны AB — это длина высоты в треугольнике AOB, которую обозначим hAOB. Для вычисления длины высоты через площадь sAOB треугольника AOB есть формула
где dAB — длина стороны AB. Формулы для вычисления площадей треугольников и длин сторон мы уже вводили. Для вычисления длин высот двух других треугольников аналогично имеем формулы
|