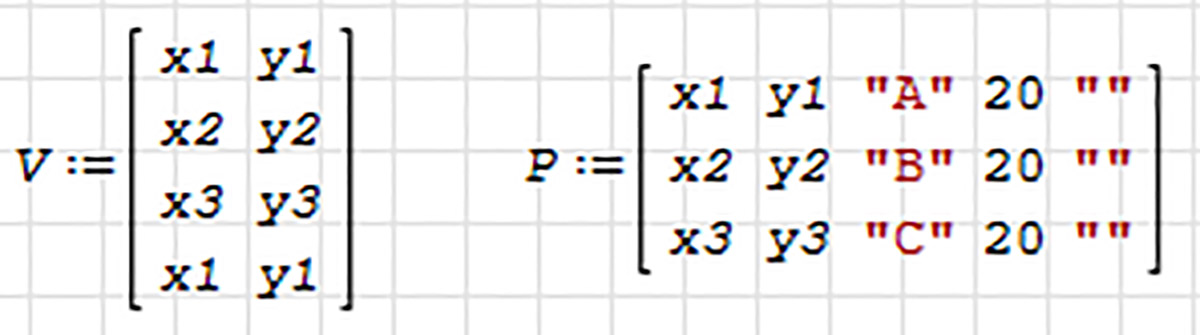§ 30. Моделирование в задачах вычисления координат замечательных точек треугольника
| Сайт: | Профильное обучение |
| Курс: | Информатика. 11 класс (Повышенный уровень) |
| Книга: | § 30. Моделирование в задачах вычисления координат замечательных точек треугольника |
| Напечатано:: | Гость |
| Дата: | Среда, 2 Июль 2025, 20:15 |
Оглавление
- 30.1. Замечательные точки треугольника
- 30.2. Постановка задачи 1 (этап 1)
- 30.3. Выбор плана создания модели (этап 2)
- 30.4. Создание документальной математической модели (этап 3а)
- 30.5. Создание компьютерной модели (этап 3б)
- 30.6. Исследование модели (этап 4)
- 30.7. Получение решения задачи 1 (этап 5)
- 30.8. Постановка задачи 2 (этап 1)
- 30.9. Выбор плана создания модели (этап 2)
- 30.10. Создание документальной математической модели (этап 3а)
- 30.11. Создание компьютерной модели (этап 3б)
- 30.12. Исследование модели и получение решения задачи 2 (этапы 4-5)
- 30.13. Постановка задачи 3 (этап 1)
- 30.14. Выбор плана создания модели (этап 2)
- 30.15. Создание документальной математической модели (этап 3а)
- 30.16. Создание компьютерной модели (этап 3б)
- 30.17. Исследование модели и получение решения задачи 3 (этапы 4-5)
- Упражнения
30.1. Замечательные точки треугольника
|
Замечательные точки треугольника — точки, положение которых однозначно определяется треугольником и не зависит от того, в каком порядке берутся стороны и вершины треугольника. Замечательных точек треугольника известно очень много (пример 30.1). Мы рассмотрим только три такие точки: - центр описанной окружности; - центр вписанной окружности; - точку пересечения медиан. |
Пример 30.1. За рубежом замечательные точки треугольника называются центрами треугольника. В интернете существует энциклопедия центров треугольника (The Encyclopedia of Triangle Centers). На начало 2021 года она включала около 40 000 описаний таких центров. Энциклопедию центров треугольников в 1994 году создал и с тех пор дополняет профессор математики университета Эвансвилла Кларк Кимберлинг. |
30.2. Постановка задачи 1 (этап 1)
| Задача 1. На координатной плоскости треугольник задан координатами своих вершин. В пакете SMath Studio построить компьютерную модель, которая позволяет вычислить координаты центра описанной окружности треугольника, а также изобразить треугольник и описанную окружность в графической области (пример 30.2). |
Пример 30.2. Будем вести построения и расчеты для треугольников, вершины которых расположены в первой четверти координатной плоскости. Для построений возьмем треугольник с вершинами: A(3;7), B(10;18), C(20;9). Модель назовем «Вычисление координат центра описанной окружности треугольника». |
30.3. Выбор плана создания модели (этап 2)
|
Поскольку программное средство для решения задачи задано, то построить, прежде всего, следует математическую модель (пример 30.3). Поэтому модель решения задачи создадим по следующему простому плану: 3а — создание документальной математической модели; 3б — создание компьютерной модели в пакете SMath Studio. |
Пример 30.3. Формулы для расчета радиуса окружности, описанной около треугольника, давно и хорошо известны. Для расчета координат центра описанной окружности можно использовать несколько математических методов, среди которых есть аналитический с построением уравнений перпендикуляров к серединам сторон и метод введения неизвестных координат центра.
|
30.4. Создание документальной математической модели (этап 3а)
|
Аналитический метод позволяет получить решение, но формулы придется выводить без помощи пакета SMath Studio (пример 30.4). Метод введения неизвестных позволяет считать двумя неизвестными координаты центра описанной окружности. Тогда три равных расстояния от центра до вершин треугольника позволят построить систему уравнений и найти значения неизвестных как решения системы. Выбираем метод введения неизвестных. Введем координаты вершин треугольника как переменные: A(x1; y1), B(x2; y2), C(x3; y3). Центр описанной окружности обозначим O (латинское) с неизвестными координатами x и y (пример 30.5). Обозначим dAO расстояние между вершиной A и центром O. Тогда Аналогично вычисляются расстояния dBO и dCO. Приравниваем пары расстояний и получаем систему двух уравнений относительно двух неизвестных x и y |
Пример 30.4. Использование аналитического метода потребует создания целого набора формул, включая уравнения сторон треугольника и уравнения серединных перпендикуляров. При этом возможности пакета SMath Studio реально будут использованы только для вычислений по полученным формулам (в качестве калькулятора) и для построения изображений треугольника и описанной окружности в графической области пакета. Пример 30.5. Переменные для координат вершин треугольника введены для того, чтобы иметь возможность использовать построенную модель для других исходных данных. Значения этих переменных координат, которые мы будем использовать в расчетах, заданы нами в примере 30.2. Введение неизвестных координат x и y для центра описанной окружности позволяет использовать формулы для вычисления расстояний между точками на координатной плоскости и построить систему достаточно сложных уравнений, чтобы передать решение этой системы пакету SMath Studio. |
30.5. Создание компьютерной модели (этап 3б)
|
Исходные данные и начало расчетной таблицы разместим по схеме, приведенной в примере 30.6. На рабочем листе всегда есть возможность подровнять верхние границы нескольких областей или их левые границы (пример 30.7). Здесь же в исходных данных чуть ниже выведем в графической области изображение треугольника. Для этого подготовим матрицу координат вершин треугольника и матрицу параметров текста.
Выводим графическую область, а в ней выводим векторы V и P (см. п. 29.4). Меняем масштаб изображения и положение осей так, чтобы в области был виден весь треугольник. Чтобы поднять букву B в графической области, во второй строке матрицы P вместо y2 запишем y2 +2. Ниже вводим заголовок «Расчеты» и формулы вычисления расстояний от вершин до центра O описанной окружности. При вводе похожих формул надо максимально использовать возможности копирования и редактирования (пример 30.8). Составляем вектор системы S, вектор неизвестных Z и вектор Zo начального приближения (см. п. 28.2), который выбирается как оценка координат центра описанной окружности. Вводим на рабочий лист вектор переменных и присваиваем ему значение функции roots(), т. е. численные значения координат центра окружности. Вектор переменных сохраняет решение системы как значения переменных x и y. Теперь в графической области нужно построить окружность и ее центр (пример 30.9). |
Пример 30.6. Схема размещения данных и заголовков модели. Пример 30.7. Чтобы выровнять верхние границы нескольких областей, их выделяют и щелкают по кнопке Пример 30.8. Заголовок и формулы вычисления расстояний от вершин до центра O. Первую формулу можно выделить, скопировать в буфер обмена и копию вставить ниже первой формулы. Во второй формуле остается исправить одну букву и два номера координат. Аналогично копированием вводится и третья формула. Пример 30.9. Полученные значения координат сохранены как значения переменных x и y, и использовать их в графической области, которая расположена на рабочем листе выше, невозможно. Поэтому построим новую графическую область ниже. Для этого выделяем вектор P и графическую область с треугольником из исходных данных, копируем их в буфер обмена и вставляем копии на лист ниже математической области, в которой получено решение системы уравнений. Щелкаем по правому нижнему углу матрицы-копии параметров текста P, нажимаем клавишу Пробел (появляется угловая метка) и дополняем матрицу P двумя строками. |
30.6. Исследование модели (этап 4)
|
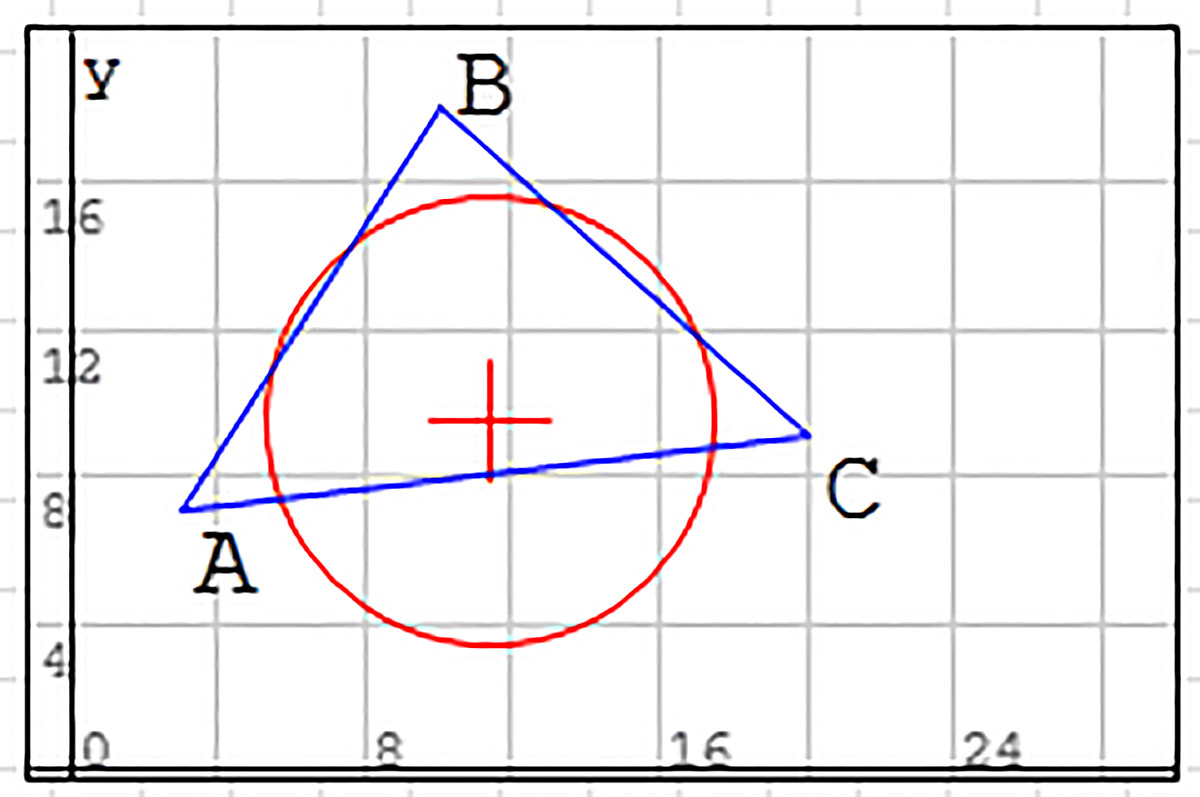
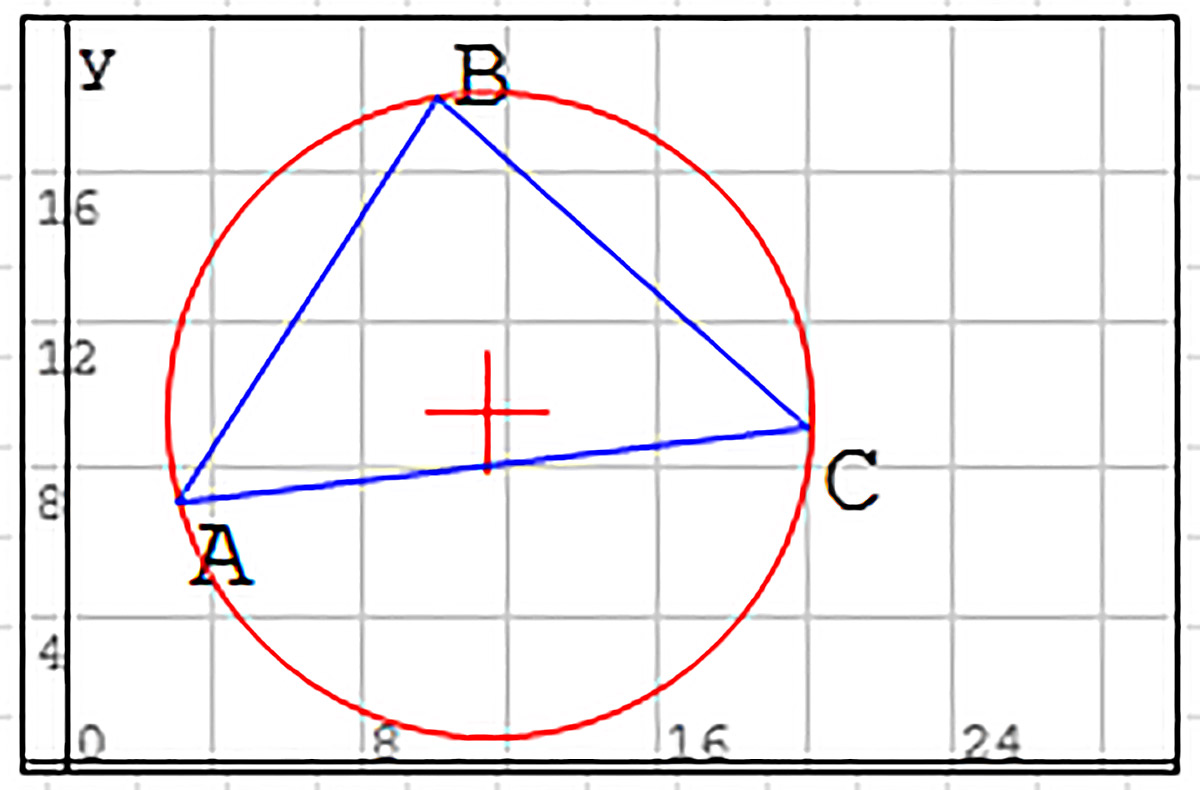
Если размер окружности, которая называется описанной, можно подобрать так, что она действительно пройдет через вершины треугольника, то это графически подтверждает адекватность построенной модели (пример 30.10). Радиус R описанной окружности в модели дают равные значения dAO, dBO и dCO. Для сравнения этот радиус можно вычислить по формуле (пример 30.11). |
30.7. Получение решения задачи 1 (этап 5)
|
Задача 1 состояла в построении компьютерной модели, и эта задача решена. При других исходных данных следует учитывать особенности модели (пример 30.12). |
Пример 30.12. Значению начального приближения Zo на координатной плоскости соответствует точка, и для любых исходных данных вектор Zo задается как вектор предполагаемых координат центра описанной окружности.
|
30.8. Постановка задачи 2 (этап 1)
| Задача 2. На координатной плоскости треугольник задан координатами своих вершин. В пакете SMath Studio построить компьютерную модель, которая позволяет вычислить координаты точки пересечения медиан треугольника, а также изобразить треугольник и эту точку пересечения в графической области (пример 30.13). |
Пример 30.13. Будем вести построения и расчеты для треугольников, вершины которых расположены в первой четверти координатной плоскости. Для построений возьмем треугольник с вершинами A(3;7), B(10;18), C(20;9). Модель назовем «Вычисление координат точки пересечения медиан треугольника». |
30.9. Выбор плана создания модели (этап 2)
|
Основу решения задачи 2 также составляет математическая модель (пример 30.14). Поэтому модель решения задачи создадим по следующему плану: 3а — создание документальной математической модели; 3б — создание компьютерной модели в пакете SMath Studio. |
Пример 30.14. Задача 2 так же, как и задача 1, имеет аналитическое решение, но в пакете SMath Studio хорошо себя показал метод введения неизвестных. Среди свойств точки пересечения медиан треугольника есть свойства, которые позволят построить модель в пакете SMath Studio с использованием метода введения неизвестных. |
30.10. Создание документальной математической модели (этап 3а)
|
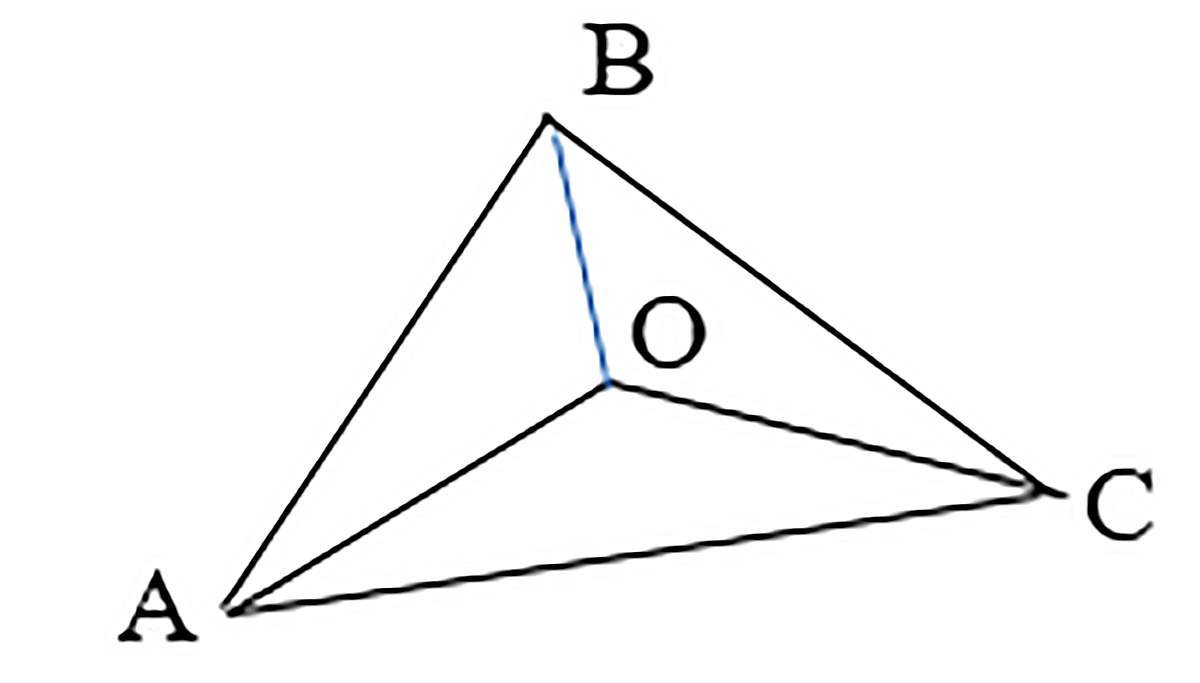
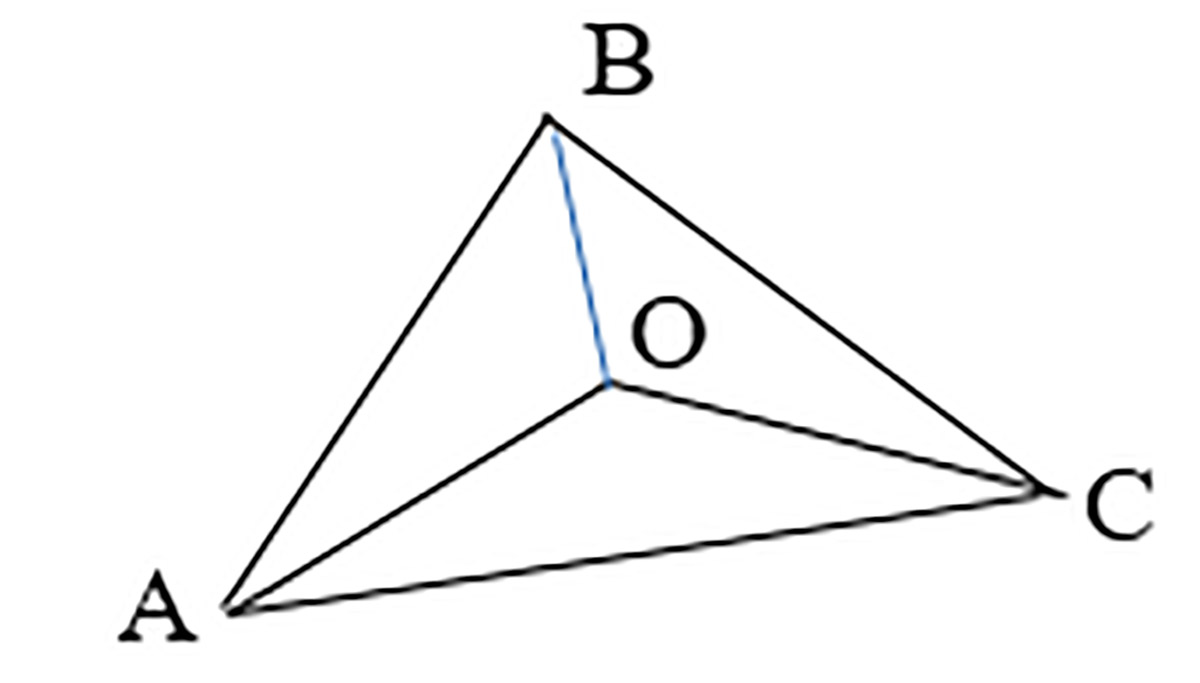
Сохраним обозначения задачи 1 для координат вершин: A(x1; y1), B(x2; y2), C(x3 ;y3), а обозначение O (латинское) с неизвестными координатами x и y используем для точки пересечения медиан треугольника. Если соединить точку O с вершинами треугольника, то получим три треугольника (пример 30.15), площади которых равны. Это свойство послужит основанием для создания системы уравнений. Для нахождения площади треугольника на координатной плоскости есть формула (пример 30.16). Приравниваем пары площадей треугольников и получаем систему двух уравнений относительно двух неизвестных, решение которой является решением задачи 2 (пример 30.17). |
Пример 30.15. Результат построений в треугольнике ABC. Пример 30.16. Формула расчета площади треугольника AOB имеет вид: sAOB = для треугольника AOC: sAOC = для треугольника BOC: sBOC = Пример 30.17. Система уравнений получит вид: |
30.11. Создание компьютерной модели (этап 3б)
|
Воспользуемся моделью задачи 1. Сохраняем ее в файле под другим именем и будем изменять. Изменяем заголовок (см. в примере 30.13), восстанавливаем исходные данные и удаляем три формулы расчета расстояний из раздела «Расчеты». На место удаленных формул вводим формулы для расчета площадей треугольников (пример 30.18). Теперь нужно изменить вектор системы S и привести его к виду
Вектор Zo начального приближения, как вектор предполагаемых координат точки пересечения медиан, можно оставить со значениями 12; 10. Получаем решение
|
Пример 30.18. Первая формула имеет вид: После ввода Остальные формулы получаются копированием предыдущей и редактированием. Пример 30.19. В нижней графической области следует удалить изображение окружности. Для этого щелкаем по правому нижнему углу матрицы параметров текста P, нажимаем клавишу Пробел. В шаблоне появляется нижняя угловая метка. Перетаскивая метку указателем мыши, удаляем последнюю строку матрицы. В ответ изображение окружности в графической области удаляется. |
30.12. Исследование модели и получение решения задачи 2 (этапы 4-5)
|
Проверку адекватности модели можно провести аналитическими расчетами (пример 30.20). Задача 2 состояла в построении компьютерной модели и эта задача решена. |
Пример 30.20. Для проведения аналитических расчетов есть несколько методов, включая вычисление координат середин сторон треугольника и построение уравнений для медиан. Получены координаты (11; 11
|
30.13. Постановка задачи 3 (этап 1)
| Задача 3. На координатной плоскости треугольник задан координатами своих вершин. В пакете SMath Studio построить компьютерную модель, которая позволяет вычислить координаты центра вписанной окружности треугольника, а также изобразить треугольник и вписанную окружность в графической области (пример 30.21). |
Пример 30.21. Будем вести построения и расчеты для треугольников, вершины которых расположены в первой четверти координатной плоскости. Для построений возьмем треугольник с вершинами: A(3;7), B(10;18), C(20;9). Модель назовем «Вычисление координат центра вписанной окружности треугольника». |
30.14. Выбор плана создания модели (этап 2)
|
Основу решения задачи 3 составляет математическая модель (пример 30.22). Поэтому модель решения задачи создадим по следующему плану: 3а — создание документальной математической модели; 3б — создание компьютерной модели в пакете SMath Studio. |
Пример 30.22. Задача 3 также имеет аналитическое решение, но в пакете SMath Studio удобнее использовать метод введения неизвестных. Среди свойств центра вписанной окружности также есть свойства, которые позволят построить модель в пакете SMath Studio с использованием метода введения неизвестных. |
30.15. Создание документальной математической модели (этап 3а)
|
Сохраним обозначения задачи 1 для координат вершин: A(x1; y1), B(x2; y2), C(x3; y3), а обозначение O (латинское) с неизвестными координатами x и y будем использовать для центра вписанной окружности. Расстояние от центра вписанной окружности до одной стороны треугольника равно расстоянию от этого центра до другой стороны и равно радиусу вписанной окружности. Это свойство послужит основанием для создания системы уравнений. Для нахождения расстояния от точки до отрезка на координатной плоскости есть формула (пример 30.23). Поскольку все три высоты равны между собой для центра вписанной окружности, приравниваем пары высот и получаем систему двух уравнений относительно двух неизвестных, решение которой является решением задачи 3.
|
Пример 30.23. Соединим отрезками центр вписанной окружности O и вершины треугольника. Расстояние от точки O до стороны AB — это длина высоты в треугольнике AOB, которую обозначим hAOB. Для вычисления длины высоты через площадь sAOB треугольника AOB есть формула
где dAB — длина стороны AB. Формулы для вычисления площадей треугольников и длин сторон мы уже вводили. Для вычисления длин высот двух других треугольников аналогично имеем формулы
|
30.16. Создание компьютерной модели (этап 3б)
|
Воспользуемся моделью задачи 1. Сохраняем ее в файле под другим именем и будем изменять. Изменяем одну букву в заголовке (см. в примере 30.21), восстанавливаем исходные данные. Изменяем первые три формулы (пример 30.24). Загружаем файл с моделью задачи 2. Открываем его, выделяем первые три формулы раздела «Расчеты», копируем в буфер обмена, открываем лист задачи 3 и вставляем формулы на лист правее первых трех. Затем под первыми тремя формулами устанавливаем указатель места ввода и, нажимая клавишу Enter, опускаем остальные формулы на 9-10 клеток вниз, освобождая место для формул вычисления длин высот (пример 30.25). Чтобы пакет выдал решение системы и построил точку центра и окружность в графической области, осталось поменять вектор S системы (пример 30.26). |
Пример 30.24. Формулу Изменяем на Аналогично вторую и третью формулы меняем для вычисления длин сторон dAC и dBC. Пример 30.25. Вводим формулы для вычисления длин высот треугольников из примера 30.23. Пример 30.26. Вектор системы задачи 1 меняем на вектор системы, полученной в п. 30.15. |
30.17. Исследование модели и получение решения задачи 3 (этапы 4-5)
|
Радиус r вписанной окружности в модели дают равные значения hAOB, hAOC и hBOC. Для сравнения этот радиус можно вычислить по другим формулам (пример 30.27). Задача 3 состояла в построении компьютерной модели, и эта задача решена. |
Пример 30.27. Для радиуса вписанной окружности известна формула
где S — площадь треугольника, а p его полупериметр. По формуле получено r = 3,967. |
Упражнения

1. Повторите на компьютере решение задачи 1, рассмотренной в параграфе.
2. Найдите решение задачи 1 для треугольника с координатами вершин: A(2; 1), B(4; 14), C(17; 8).
3. Повторите на компьютере решение задачи 2, рассмотренной в параграфе.
4. Найдите решение задачи 2 для треугольника с координатами вершин: A(1; 3), B(15; –11), C(8; 15).
5. Повторите на компьютере решение задачи 3, рассмотренной в параграфе.
6. Найдите решение задачи 3 для треугольника с координатами вершин: A(1; –4), B(12; 14), C(16; –10).
7. Треугольник задан координатами своих вершин. Используя SMath Studio, найти координаты точки пересечения его высот (ортоцентр) и изобразить треугольник с ортоцентром в графической области.
Указание. Если вершины треугольника обозначить A, B и C, точку пересечения высот обозначить O, а высоты обозначить AD, BE и CF, то построить систему уравнений позволит известное равенство для длин частей высот dAO·dOD = dBO·dOE = dCO·dOF.
8. Дан прямоугольник ABCD со сторонами 5 и 15. Внутренняя точка прямоугольника P соединена с вершинами прямоугольника отрезками прямых, при этом угол между отрезками DP и CP равен 150°, а угол между отрезками CP и BP равен 45°. Используя SMath Studio, найти длину отрезка AP и построить чертеж в графической области.
Указание. Построить прямоугольник на координатной плоскости, чтобы его вершины получили координаты. Через неизвестные координаты точки P выразить угловые коэффициенты прямых, на которых лежат отрезки DP, CP и BP. Угловые коэффициенты прямых являются тангенсами неких углов. Разность одной пары углов равна 150°, а второй пары — 45°. Для вычисления тангенса разности углов есть формула. Две формулы дадут два уравнения для угловых коэффициентов. Эти уравнения и образуют систему. Для получения решения системы уравнений компоненты вектора Zo надо выбирать как координаты предполагаемого положения точки P. Вычислить длину отрезка AP по координатам его концов. Построить чертеж.
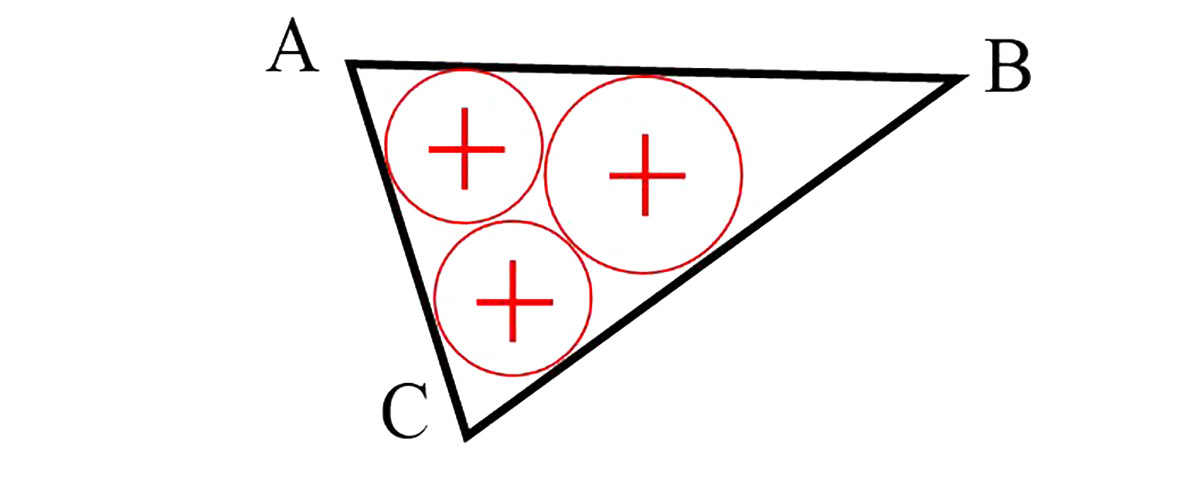
9*. Треугольник задан координатами своих вершин. Используя SMath Studio, найти координаты центров и радиусы трех окружностей, которые вписаны в треугольник и касаются друг друга, а также построить треугольник и окружности в графической области.