§ 30. Моделирование в задачах вычисления координат замечательных точек треугольника

30.10. Создание документальной математической модели (этап 3а)

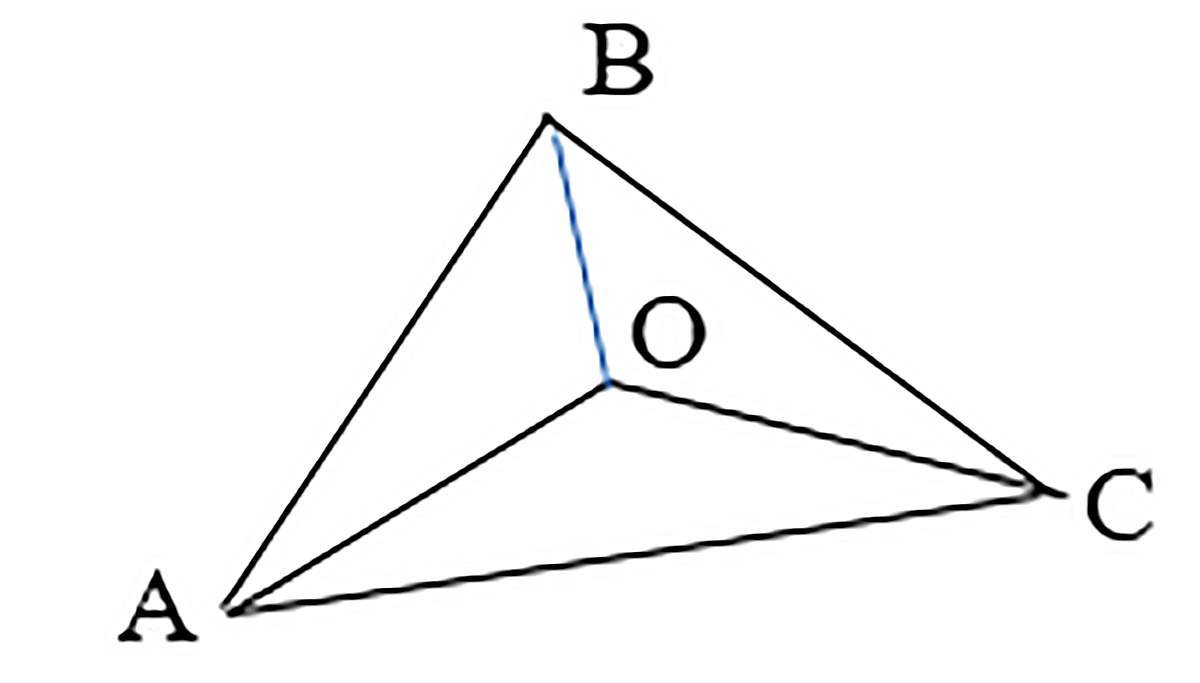
Сохраним обозначения задачи 1 для координат вершин: A(x1; y1), B(x2; y2), C(x3 ;y3), а обозначение  O (латинское) с неизвестными координатами x и y используем для точки пересечения медиан треугольника.

Если соединить точку O с вершинами треугольника, то получим три треугольника (пример 30.15), площади которых равны. Это свойство послужит основанием для создания системы уравнений.

Для нахождения площади треугольника на координатной плоскости есть формула (пример 30.16).

Приравниваем пары площадей треугольников и получаем систему двух уравнений относительно двух неизвестных, решение которой является решением задачи  2 (пример 30.17).

Пример 30.15. Результат построений в треугольнике ABC.

Пример 30.16. Формула расчета площади треугольника AOB имеет вид:

sAOB = |(y – y1)(x2 – x1) – (x –x1)(y2 – y1)|,

для треугольника AOC:

sAOC = |(y – y1)(x3 – x1) – (x – x1)(y3 – y1)|,

для треугольника BOC:

sBOC =  |(y – y2)(x3 – x2) – (x – x2)(y3 – y2)|.

Пример 30.17. Система уравнений получит вид:

Численное решение системы даст значения координат x и y точки пересечения медиан.