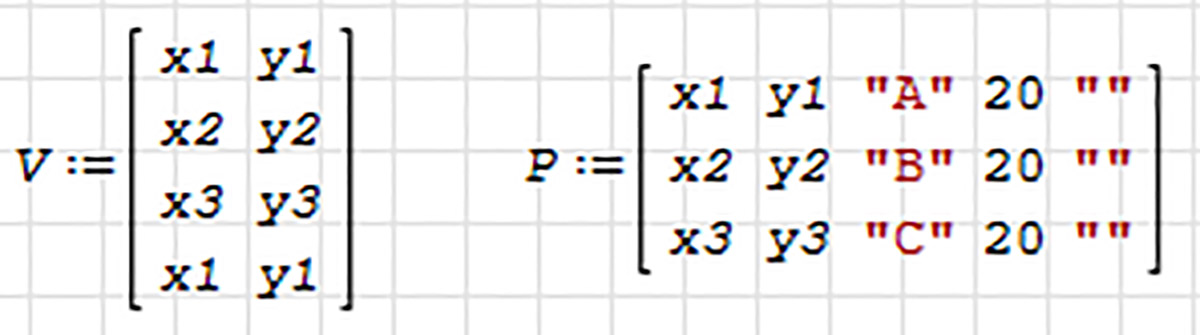§ 30. Моделирование в задачах вычисления координат замечательных точек треугольника
30.5. Создание компьютерной модели (этап 3б)
|
Исходные данные и начало расчетной таблицы разместим по схеме, приведенной в примере 30.6. На рабочем листе всегда есть возможность подровнять верхние границы нескольких областей или их левые границы (пример 30.7). Здесь же в исходных данных чуть ниже выведем в графической области изображение треугольника. Для этого подготовим матрицу координат вершин треугольника и матрицу параметров текста.
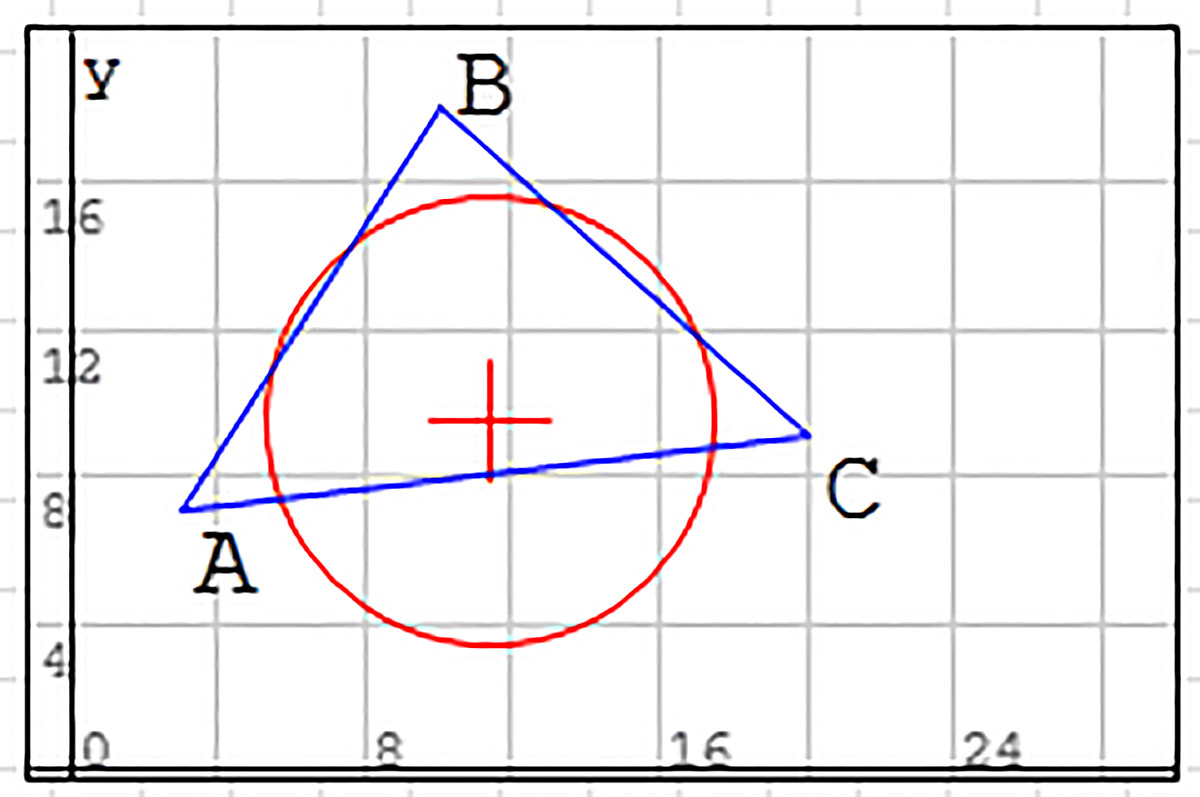
Выводим графическую область, а в ней выводим векторы V и P (см. п. 29.4). Меняем масштаб изображения и положение осей так, чтобы в области был виден весь треугольник. Чтобы поднять букву B в графической области, во второй строке матрицы P вместо y2 запишем y2 +2. Ниже вводим заголовок «Расчеты» и формулы вычисления расстояний от вершин до центра O описанной окружности. При вводе похожих формул надо максимально использовать возможности копирования и редактирования (пример 30.8). Составляем вектор системы S, вектор неизвестных Z и вектор Zo начального приближения (см. п. 28.2), который выбирается как оценка координат центра описанной окружности. Вводим на рабочий лист вектор переменных и присваиваем ему значение функции roots(), т. е. численные значения координат центра окружности. Вектор переменных сохраняет решение системы как значения переменных x и y. Теперь в графической области нужно построить окружность и ее центр (пример 30.9). |
Пример 30.6. Схема размещения данных и заголовков модели. Пример 30.7. Чтобы выровнять верхние границы нескольких областей, их выделяют и щелкают по кнопке Пример 30.8. Заголовок и формулы вычисления расстояний от вершин до центра O. Первую формулу можно выделить, скопировать в буфер обмена и копию вставить ниже первой формулы. Во второй формуле остается исправить одну букву и два номера координат. Аналогично копированием вводится и третья формула. Пример 30.9. Полученные значения координат сохранены как значения переменных x и y, и использовать их в графической области, которая расположена на рабочем листе выше, невозможно. Поэтому построим новую графическую область ниже. Для этого выделяем вектор P и графическую область с треугольником из исходных данных, копируем их в буфер обмена и вставляем копии на лист ниже математической области, в которой получено решение системы уравнений. Щелкаем по правому нижнему углу матрицы-копии параметров текста P, нажимаем клавишу Пробел (появляется угловая метка) и дополняем матрицу P двумя строками. |