§ 24. Задачи раскроя
24.5. Создание компьютерной расчетной модели с минимизацией расхода (этап 3б)
|
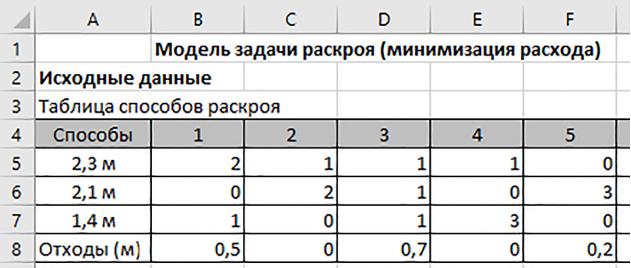
Исходные данные компьютерной модели разместим по схеме, приведенной в примере 24.6. В столбце справа от таблицы способов раскроя введем задания заказа по схеме примера 24.7. Расчетную таблицу будем строить по схеме, приведенной в примере 24.8. В ячейку А15 вводится формула суммы значений ячеек строки 14 таблицы плана способов раскроя. В результате в ячейке вычисляется число израсходованных по плану бревен. В ячейку A16 вводится функция СУММПРОИЗВ(), которая возвращает сумму произведений ячеек диапазонов $B$14:$I$14 и диапазона B5:I5 (пример 24.9). В результате в ячейке A16 отображается число заготовок длиной 2,3 м, изготовленных по плану. Затем формулой ячейки A16 заполняется вниз диапазон A17:A19. В результате в ячейках диапазона будут отображаться числа, которые соответствуют подписям справа. Оценим теперь созданную модель с математической точки зрения. Требуется найти план способов раскроя — это значения ячеек диапазона B14:I14. Искомый план должен минимизировать расход исходных материалов — это значение ячейки A15. В диапазоне J5:J7 размещены объемы заготовок, требуемые в заказе, а в диапазоне A16:A18 — плановые объемы заготовок, которые должны быть не меньше объемов заказа. Это уже ограничения. К ограничениям следует добавить требования, чтобы значения ячеек диапазона B14:I14 (плановые объемы) были целыми и неотрицательными. Фактически мы получили экстремальную задачу поиска плана раскроя, который минимизирует целевую функцию в ячейке A15 при ограничениях. В электронных таблицах задача решается с помощью надстройки Поиск решения, которую мы уже использовали. На вкладке Данные кнопкой Поиск решения необходимо вызвать окно Параметры поиска решения и ввести исходные данные для поиска. Целевая функция размещена в ячейке A15, критерий — Минимум, изменяя ячейки переменных диапазона B14:I14 (плановые объемы). Переходим к вводу ограничений (пример 24.10). В разделе Выберите метод решения выбираем Поиск решения лин. задач симплекс-методом и щелкаем по кнопке Найти решение. |
Пример 24.6. Схема размещения исходных данных компьютерной модели. На схеме столбцы G, H, I не показаны. Столбец A нужно расширить.
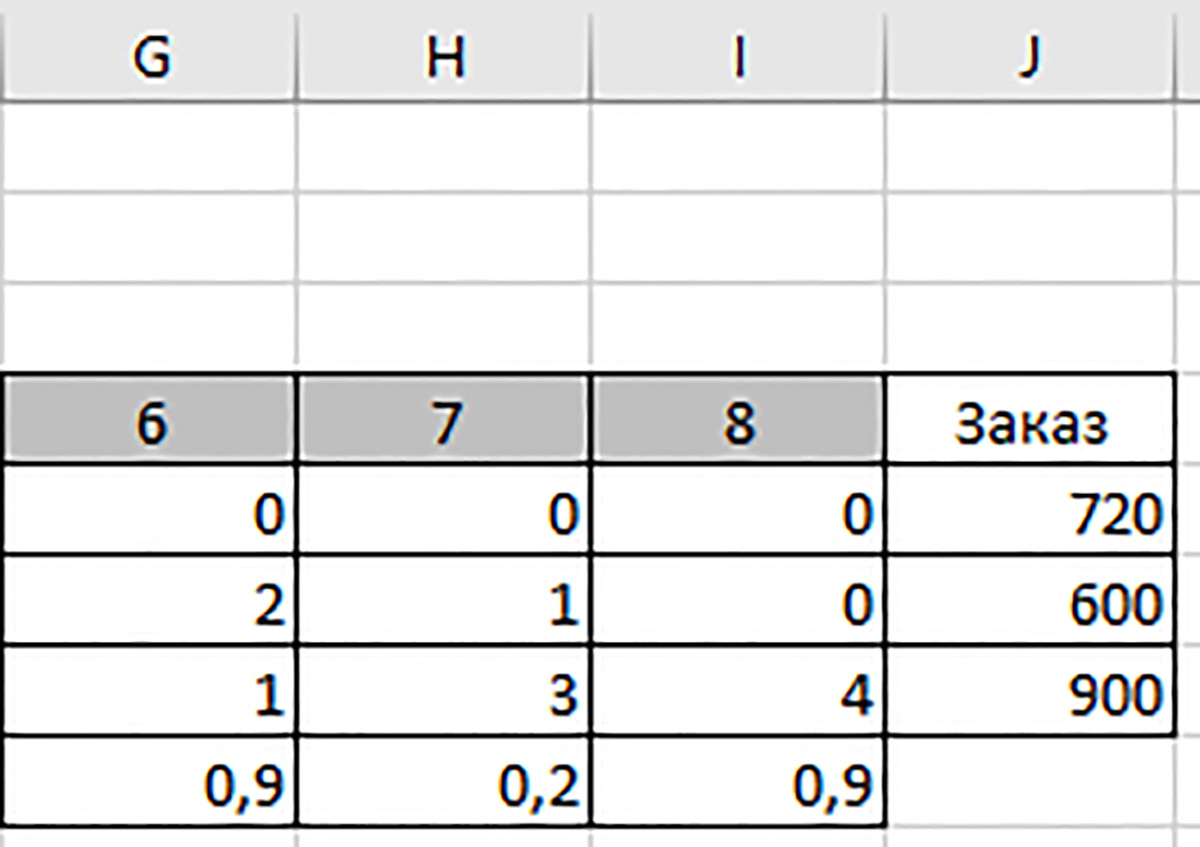
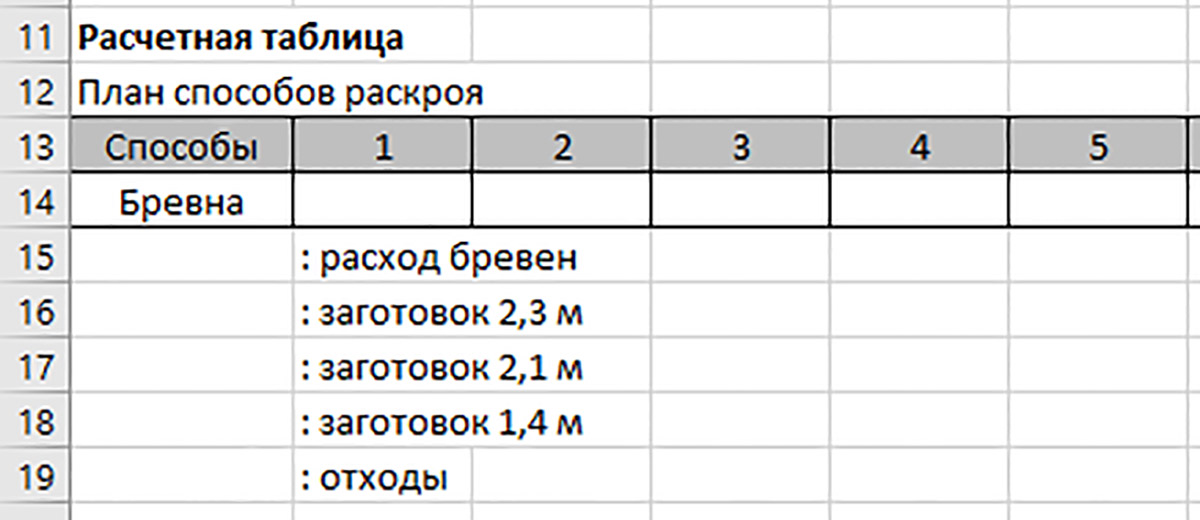
Пример 24.7. Дополнение таблицы исходных данных заданиями заказа. Пример 24.8. Схема размещения расчетной таблицы компьютерной модели задачи раскроя. На схеме столбцы G, H, I не показаны. Подписи ниже таблицы вводятся в ячейки столбца B. Пример 24.9. Табличный курсор устанавливаем на ячейку A16, щелчком по кнопке Вставить функцию в строке формул открываем окно Вставка функции. Проводим поиск функции по ее имени, затем дважды щелкаем по ее имени в списке. Открывается окно для ввода аргументов. В таблице плана способов раскроя выделяем диапазон B14:I14. Он записывается в поле аргумента Массив1. Изменяем относительные ссылки диапазона B14:I14 на абсолютные $B$14:$I$14. Затем в окне щелкаем по полю второго аргумента Массив2 и в таблице способов раскроя выделяем диапазон B5:I5. Щелчком по кнопке OK завершаем ввод. Пример 24.10. Щелкаем по кнопке Добавить. В новом окне для ввода ограничений в левое поле выделяем в модели диапазон A16:A18. Во втором поле выбираем знак больше или равно. В третье поле вводим диапазон J5:J7 из модели. Щелкаем по кнопке OK. Чтобы значения ячеек диапазона B14:I14 стали целыми числами, следует в диалоговом окне Добавление ограничений слева ввести диапазон B14:I14, а в центральном поле выбрать обозначение «цел». Щелкаем по кнопке OK. Под полем для ограничений должна стоять галочка выбора пункта Сделать переменные без ограничений неотрицательными. |