§ 2. Пружинный и математический маятники
|
Груз, подвешенный на нити, колеблющийся в поле тяжести Земли, а также груз, прикрепленный к пружине — примеры наиболее простых механических колебательных систем. Рассмотрим физические процессы, происходящие в таких системах. |
Совокупность нескольких тел образуют механическую систему. Тела, не входящие в систему, называются внешними.
Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое телом под действием приложенных к нему сил, обратно пропорционально массе тела, направлено по результирующей этих сил и прямо пропорционально ее модулю:
Закон Гука: при упругих деформациях сжатия и растяжения модуль силы упругости прямо пропорционален модулю изменения длины тела:
где k — жесткость тела, — длина недеформированного тела, l — длина деформированного тела. Направление силы упругости всегда противоположно направлению смещения при деформации.
Какие условия необходимы для возникновения колебаний?
Результаты опытов показывают, что для возникновения и существования механических колебаний тело изначально необходимо привести в движение. Это можно сделать, отклоняя его от положения равновесия или придавая ему начальную скорость посредством толчка. Этим отклонением или толчком определяется амплитуда колебаний. Кроме того, при выведении тела из положения равновесия в колеблющейся системе должна возникать результирующая сила, стремящаяся возвратить тело в положение равновесия.
Простейшая колебательная система, состоящая из тела с прикрепленной к нему пружиной, связывающей тело и опору, называется пружинным маятником. Пружина может располагаться как горизонтально (горизонтальный пружинный маятник), так и вертикально (вертикальный пружинный маятник).
Рассмотрим колебания горизонтального пружинного маятника.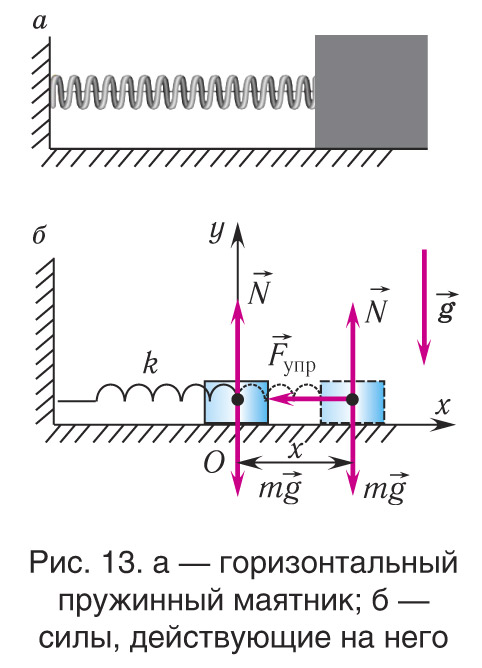
Пусть тело массой m, лежащее на гладкой горизонтальной поверхности, прикреплено к свободному концу невесомой пружины жесткостью k (рис. 13, а). Второй конец пружины прикреплен к неподвижной опоре. Выведем тело из положения равновесия, сместив его, например, вправо на расстояние x (см. рис. 13, б). При этом согласно закону Гука возникнет сила упругости приложенная к телу и направленная влево.
Согласно второму закону Ньютона будет выполняться равенство:
|
|
(1) |
С учетом закона Гука из (1) получаем уравнение для проекций величин на ось Ox (см. рис. 13, б):
|
|
(2) |
Согласно (2) ускорение тела массой m пропорционально действующей силе и направлено к положению равновесия. При этом возникают колебания тела. Каждые полпериода направление движения меняется на противоположное. Смещение груза происходит то вправо, то влево относительно положения равновесия, т. е. оно меняет знак. Следовательно, и сила согласно (2) тоже меняет знак.
Перепишем полученное соотношение (2) в виде:
|
|
(3) |
Уравнение (3) называется уравнением гармонических колебаний пружинного маятника.
Следовательно, необходимым условием возникновения гармонических колебаний является действие возвращающей силы, направленной к положению равновесия и прямо пропорциональной смещению тела от положения равновесия. Эта возвращающая сила всегда направлена к положению равновесия, о чем «говорит» минус в уравнении (2).
В положении равновесия возвращающая сила равна нулю ( = 0), так как x = 0. Поэтому если в этом положении колеблющееся тело остановить, то колебания исчезнут.
Расчеты показывают, а результаты экспериментов подтверждают, что при описанных условиях тело будет совершать колебания с периодом:
| (4) |
С учетом того, что период связан с циклической частотой соотношением , находим:
| (5) |
Из формул (4) и (5) следует, что период и частота гармонических колебаний пружинного маятника определяются массой груза m и жесткостью пружины k и не зависят от амплитуды его колебаний.
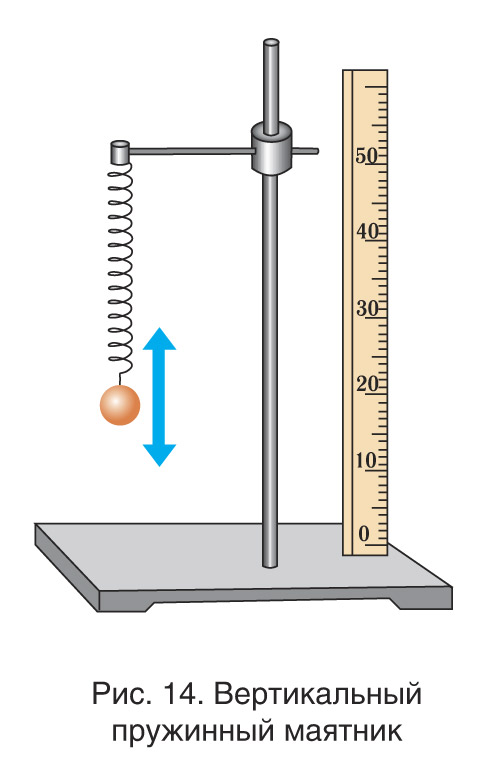
Отметим, что период и циклическая частота колебаний вертикального пружинного маятника (рис. 14) также определяются по формулам (4) и (5).
Одной из наиболее распространенных колебательных систем является математический маятник.
Математическим маятником называется небольшое тело массой m, подвешенное на невесомой нерастяжимой нити длиной l, находящееся в поле силы тяжести (рис. 15).
Рассмотрим колебания математического маятника.
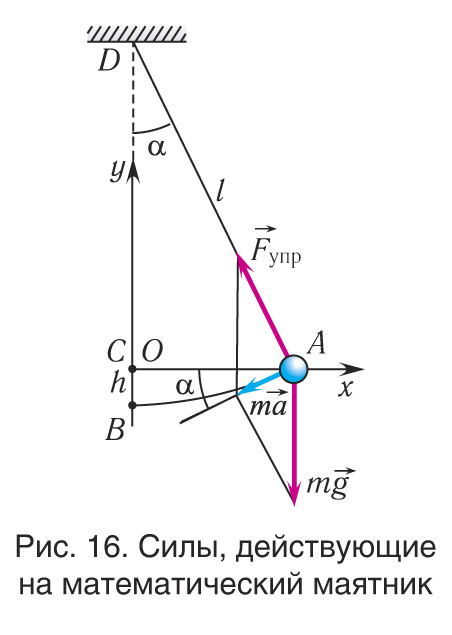
Отклонение маятника от положения равновесия будем характеризовать углом α (рис. 16), который нить образует с вертикалью. После отклонения маятника от положения равновесия на него действуют две силы: направленная вертикально вниз сила тяжести и направленная вдоль нити сила упругости
. Под действием этих сил тело движется ускоренно к положению равновесия (точка B). Пройдя точку B, тело продолжает двигаться, но его скорость постепенно уменьшается, обращаясь в нуль в точке, симметричной точке А относительно вертикали. После этого оно начинает двигаться обратно к точке B.
Согласно второму закону Ньютона для движения маятника можем записать:
| (6) |
В проекциях на выбранные оси координат Ox и Oy (см. рис. 16) получаем:
| (7) |
| (8) |
Поскольку при малых углах отклонения длина дуги АВ ≈ х, то из ΔAOD находим:
,
где х — отклонение маятника от положения равновесия, l — длина маятника. Подставляя выражение для синуса в (7), получим:
| (9) |
Таким образом, силой, возвращающей маятник к устойчивому положению равновесия при колебаниях, являются силы упругости его нити и силы тяжести.
При малых углах отклонения маятника проекция вектора ускорения и ей можно пренебречь, а
, тогда из уравнения (8) следует
Следовательно, уравнение движения маятника вдоль оси Ox запишется в виде:
где — проекция ускорения, сообщаемого грузу маятника силой упругости нити.
Откуда получаем уравнение колебаний математического маятника:
|
|
(10) |
Сравнивая соотношения (10), (3) и (5), легко получить формулу для циклической частоты математического маятника в поле тяжести Земли:
| (11) |
Период малых колебаний математического маятника в поле тяжести Земли определяется по формуле Гюйгенса:
| (12) |
Используя соотношения (5) и (11), уравнение колебаний пружинного маятника и математического маятника
можно записать в одинаковом виде:
| (13) |
Таким образом, зависимости координат от времени x(t), описываемые уравнениями (5) и (6) из § 1, удовлетворяют уравнению (13), которое называется уравнением гармонических колебаний.
Как видно из формул (11), (12), период и циклическая частота малых колебаний математического маятника не зависят от массы маятника и амплитуды его колебаний, а определяются только его длиной и ускорением свободного падения.
Галилео Галилей первый экспериментально определил, что период малых колебаний () математического маятника длиной l в поле силы тяжести не зависит от его массы m и амплитуды колебаний (угла начального отклонения a).
  |
Одним из важнейших достижений Х. Гюйгенса было изобретение часов с маятником. Он запатентовал свое изобретение 16 июля 1657 г. В 1673 г. вышло в свет его сочинение «Маятниковые часы», в котором были изложены теоретические основы его изобретения. Именно постоянство периода (частоты) колебаний маятника позволило использовать его для создания часов.
Если маятник приобретает дополнительное ускорение , обусловленное, например, ускоренным движением точки подвеса, то при этом будет изменяться сила упругости нити. В таком случае период колебаний маятника будет определяться по формуле:
где — «эффективное ускорение», равное векторной разности
.
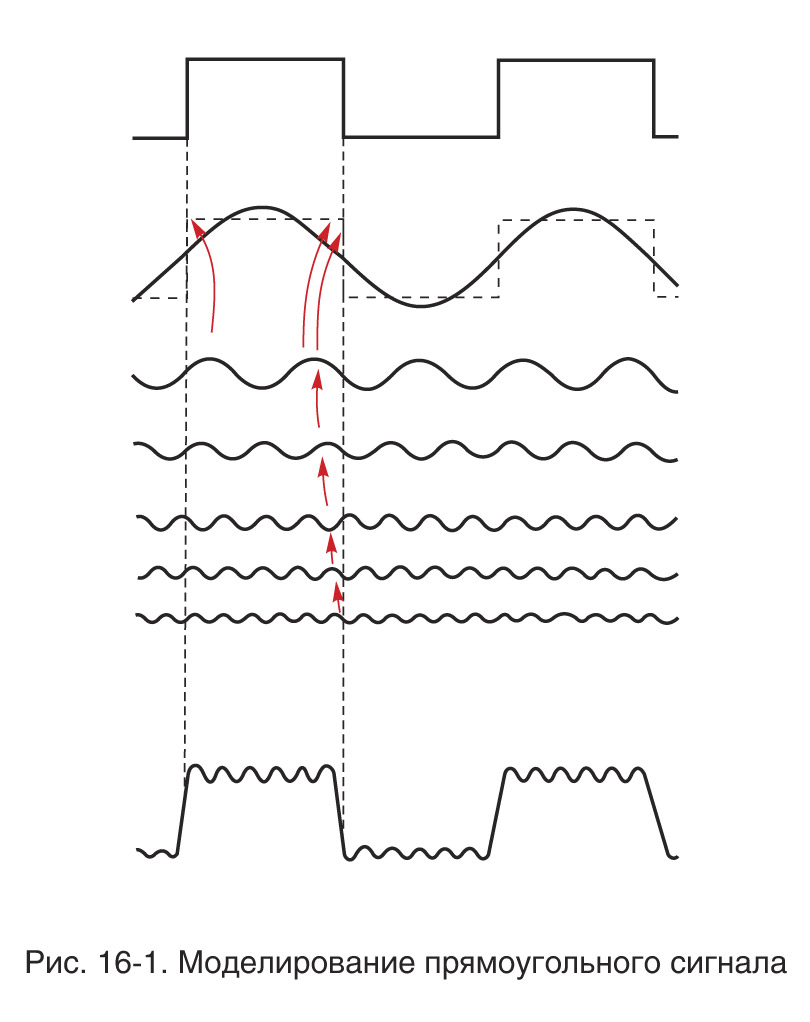
Повышенный интерес к гармоническим колебаниям объясняется тем, что они широко распространены в науке и технике (маятники, музыкальные инструменты, свет, переменные токи и т. д.). Кроме того, гармонические колебания имеют простое математическое описание, а их период не зависит от амплитуды. Подчеркнем, что любое периодическое движение можно рассматривать как результат наложения простых гармонических составляющих.
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греческих слов εσος (изос) — равный и χρονος (хронос) — время). Следовательно, колебания пружинного маятника обладают свойством изохронности. Изохронность колебаний маятника была открыта Галилео Галилеем в