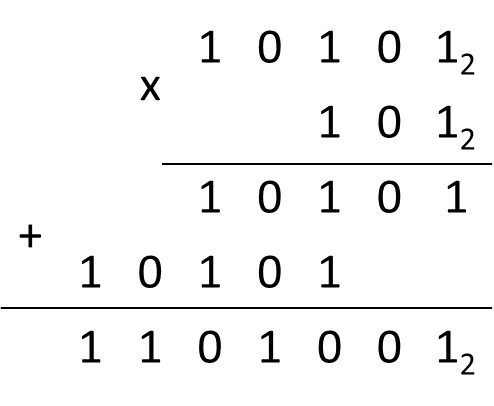|
Правила выполнения арифметических действий (сложения, вычитания, умножения и деления) в десятичной системе счисления хорошо известны. Эти же правила применимы к выполнению арифметических действий и в других позиционных системах счисления.
В примере 25.5 рассмотрены правила выполнения поразрядных арифметических действий в двоичной системе счисления.
Рассмотрим алгоритмы выполнения каждого из арифметических действий в позиционных системах счисления с произвольным основанием .
Сложение
Чтобы в системе счисления с основанием получить сумму S двух чисел A и B, нужно просуммировать образующие их цифры по разрядам от младшего разряда к старшему по следующим правилам:
- Если ai + bi < p, то , si = ai + bi значение (i + 1)-ого разряда не изменяется.
- Если ai + bi ≥ p, то , si = ai + bi – p, значение ( i + 1)-ого разряда увеличивается на 1. Это связано с тем, что единиц i-го разряда соответствует одной единице ( i + 1)-го разряда, а в каждом разряде не может находиться более (p – 1) единиц.
Пример 25.6. Сложить числа 11112 и 1012.
- Складываем значения в нулевых разрядах слагаемых: 1 + 1 = 102. Записываем 0 и 1, переносим в первый разряд.
- В первых разрядах складываем: 1 + 0 = 1 и добавляем 1 из нулевого разряда. Получаем 1 + 0 + 1 = 102. Записываем 0, а 1 переносим во второй разряд.
- Складываем значения во вторых разрядах: 1 + 1 + 1 = 3(112), 3 ≥ 2, значит, записываем 1, и 1 переносим в третий разряд.
- Вычисляем в третьем разряде: 1 + 1 = 2. Так как 2 ≥ 2, то записываем 0, а 1 переносим в четвертый разряд.
В примере 25.7 выполнено сложение двоичных смешанных чисел.
Пример 25.8. Сложить числа 63548 и 7438.
- Вычисляем: 4 + 3 = 7.
- Складываем: 5 + 4 = 9. 9 ≥ 8, значит, записываем 1 (так как 9 – 8 = 1), а 1 переносим во второй разряд.
- Вычисляем: 3 + 7 = 10. Добавляем 1 из первого разряда 10 + 1 = 11. 11 ≥ 8, значит, записываем 3 (11 – 8 = 3 ), а 1 переносим в третий разряд.
- В третьем разряде: 6 + 1 = 7.
Пример 25.9. Сложить числа 5B416 и C5216.
- В нулевом разряде: 4 + 2 = 6.
- Вычисляем: B(11) + 5 = 16. 16 ≥ 16, значит, записываем 0 (16 – 16 = 0), а 1 переносим во второй разряд.
- Складываем: 5 + C(12) = 17. Добавляем 1 из второго разряда: 17 + 1 = 18. 18 ≥ 16, значит, записываем 2 (18 – 16 = 2), а 1 переносим в третий разряд.
Вычитание
Чтобы в системе счисления с основанием получить разность R двух чисел A и B ( A > B), нужно вычислять разности образующих их цифр по разрядам i от младшего к старшему по следующему правилу:
- Если ai ≥ bi, то ri = ai – bi, значение в (i + 1 )-м разряде не изменяется.
- Если ai < bi, то ri = p + ai – bi, то значение в (i + 1 )-м разряде уменьшается на 1. При этом, если ai = 0, то занимаем одну разрядную единицу (равную основанию системы счисления p) в (i + 1)-м разряде и продолжаем занимать до ближайшего к i-му старшего разряда (включительно), где ai ≠ 0.
Пример 25.10. Найти разность чисел 10002 и 112.
- В нулевом разряде: 0 < 1. Занимаем в первом разряде. Так как в двух следующих разрядах записан 0, то продолжаем занимать до третьего разряда, где записано 1. Получаем 2 – 1 = 1 (102 – 12 = 12). В результат записываем 1.
- В первом разряде после того, как заняли, осталось 1 (2(102) – 1). Вычитаем: 1 – 1 = 0. В результат записываем 0.
- Во втором разряде осталось 1. Вычитаем: 1 – 0 = 1. В результат записываем 1.
- В третьем разряде остается 0.
Пример 25.11. Найти разность чисел 74508 и 7368.
- В нулевом разряде: 0 < 6. Занимаем в первом разряде 8(108). Вычитаем: 8 – 6 = 2. В результат записываем 2.
- В первом разряде осталось 4. Вычитаем: 4 – 3 = 1. В результат записываем 1.
- Во втором разряде: 4 < 7. Занимаем в третьем разряде 8. Вычисляем: 8 + 4 – 7 = 5. В результат записываем 5.
- В третьем разряде остается 6, что и записываем в результат.
В примере 25.12 рассмотрено вычитание чисел в шестнадцатеричной системе счисления, которое выполняется по аналогичному алгоритму.
Умножение
Чтобы в системе счисления с основанием p получить произведение М числа A и числа B < p, надо вычислить произведение цифр числа А по разрядам от младшего к старшему и числа В в соответствии с правилами:
- Если ai · b < p, то mi = ai · b и значение в (i + 1)-м разряде не изменяется.
- Если ai · b < p, то mi = ai · b modp, а значение в ( i + 1 )-м разряде увеличивается на ai · b divp.
Пример 25.13. Найти произведение чисел 12123 и 23.
- Вычисляем: 2 · 2 = 4. Так как 4 ≥ 3, в результат записываем 4 mod 3 = 1. Значение в первом разряде увеличиваем на 4 div 3 = 1.
- Вычисляем: 1 · 2 + 1 = 3, 3 ≥ 3, значит, в результат записываем 3 mod 3 = 0, а второй разряд увеличиваем на 3 div 3 = 1.
- Вычисляем: 2 . 2 + 1 = 5. В результат записываем 5 mod 3 = 2. Третий разряд увеличиваем на 5 div 3 = 1.
- Повторяем п. 2. В третьем разряде результата записываем 0, а в четвертом — 1.
В примерах 25.14 и 25.15 по аналогичному алгоритму выполнено умножение многозначного числа на однозначное число в других системах счисления.
Умножение многозначного числа на многозначное число выполняется столбиком. При этом два множителя располагаются один под другим так, чтобы разряды чисел совпадали (находились в одном столбце).
В примерах 25.16 и 25.17 выполнено умножение многозначного числа на многозначное число.
*Деление
Операцию деления нельзя свести к поразрядным операциям над цифрами, составляющими число. Деление чисел в системе счисления с произвольным основанием выполняется так же, как и в десятичной системе счисления. А это значит, что при выполнении деления применяются правила умножения и вычитания чисел в системе счисления с основанием p. В отличие от других арифметических действий деление выполняется начиная со старшего разряда делимого.
Пример 25.18. Найти частное чисел 1010102 и 1112.
- Сравниваем значение в самом старшем разряде и делитель. Если делитель больше значения в данном разряде, то рассматриваем это значение и значение в следующем разряде как число. Повторяем операцию до момента, когда полученное число сравняется либо превысит значение делителя ( 1 < 111, 10 < 111, 101 < 111, 1010 > 111).
- Подбираем такое число (1), при котором произведение делителя и этого числа (111) будет максимально близким по значению (но не больше) к числу, полученному в п. 1. Записываем это число в частное первым.
- Вычитаем произведение (п. 2) от числа, образованного значениями выбранных разрядов (1010 – 111).
- Остаток пишем после черты (11).
- Сносим значение следующего разряда к остатку (1) и проверяем, больше или равно получившееся число (111) делителя. Если нет, то сносим значение еще одного разряда до тех пор, пока не образуется число больше или равное делителя, при этом не забываем записывать нули в частное.
- Проделываем все вышеперечисленное до тех пор, пока цифры в делимом не закончатся или в остатке не получится число меньше делителя.
Пример 25.19. Найти частное чисел 133518 и 1638.
- Сравниваем:1 < 163, 13 < 163, 133 < 163. 1335 > 163.
- Подбираем: 6 · 163 = 1262 < 1335.
- Вычитаем: 1335 – 1262 = 53.
- Сносим 1 и получаем 531 > 163.
- Подбираем: 3 . 163 = 531.
- Вычитаем: 531 – 531 = 0.
Пример 25.20. Найти частное чисел 8D2F6C16 и DF16.
- Сравниваем: 8 < DF, 8D < DF, 8D2 > DF.
- Подбираем: А . DF = 8B6 < 8D2.
- Вычитаем: 8D2 – 8B6 = 1C.
- Сносим F и получаем 1CF > DF.
- Подбираем: 2 . DF = 1BE < 1CF.
- Вычитаем: 1CF – 1BE = 11.
- Сносим 6 и получаем 116 > DF.
- Подбираем: 1 . DF = DF.
- Вычитаем: 116 – DF = 37.
- Сносим C и получаем 37C > DF.
- Подбираем: 4 . DF = 37C.
- Вычитаем: 37C – 37C = 0.
|
В компьютерных устройствах выполнение любого действия основано на использовании простейших микроопераций – сложение и сдвиг (операция вычитания сводится к операции сложения). Это позволяет иметь единое арифметико-логическое устройство для выполнения операций, связанных с обработкой данных.
Пример 25.5. Правила двоичной арифметики.
1. Сложение.

2. Вычитание.

3. Умножение.

Пример 25.6. Сложение целых чисел в двоичной системе счисления.
11112 + 1012 = x2
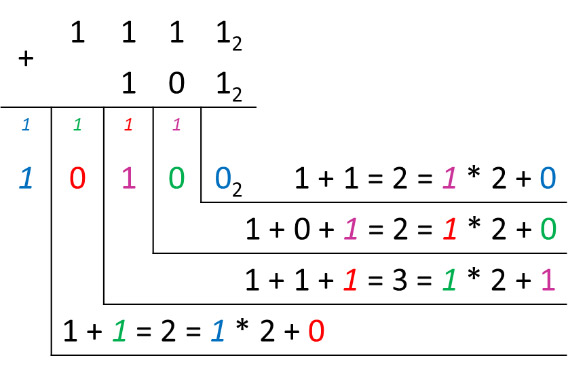
Ответ: 101002
Пример 25.7. Сложение смешанных чисел в двоичной системе счисления.
101,10012 + 1,11112 = x2
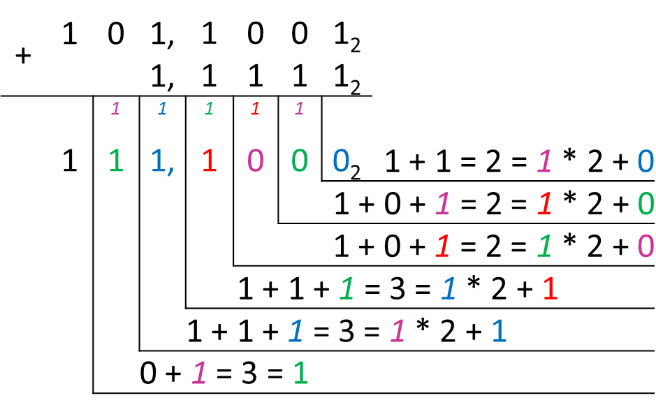
Ответ: 111,12
Пример 25.8. Сложение чисел в восьмеричной системе счисления.
63548 + 7438 = x8
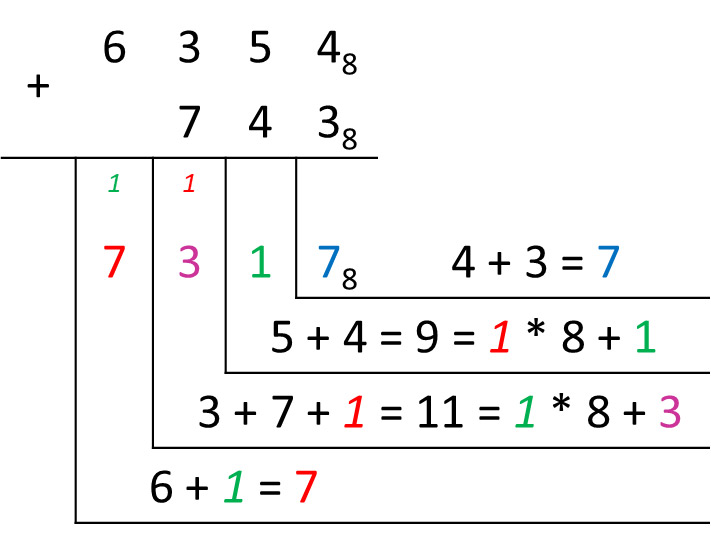
Ответ: 73178
Пример 25.9. Сложение чисел в шестнадцатеричной системе счисления.
5B416 + C5216 = x16
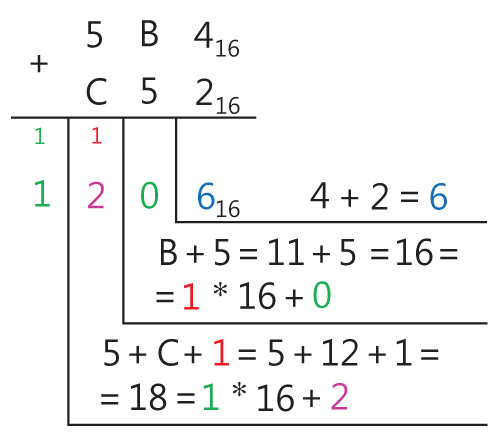
Ответ: 120616
Пример 25.10. Вычитание чисел в двоичной системе счисления.
10002 – 112 = x2
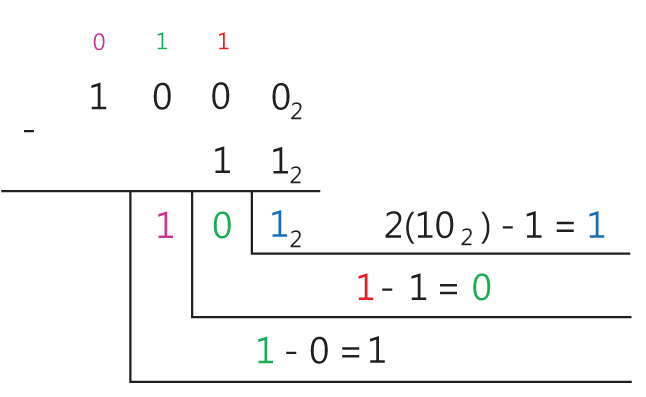
Ответ: 1012
Пример 25.11. Вычитание чисел в восьмеричной системе счисления.
74508 – 7368 = x8
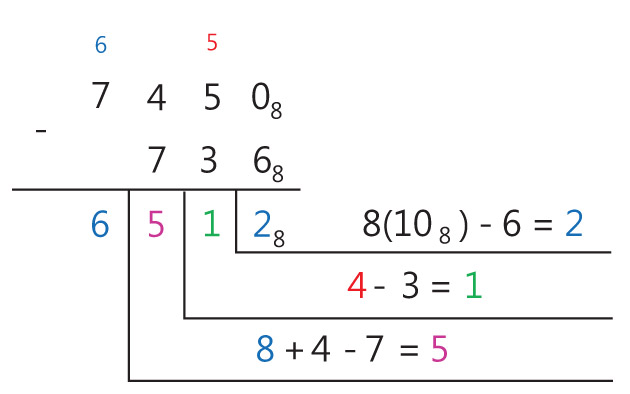
Ответ: 65128
Пример 25.12. Вычитание чисел в шестнадцатеричной системе счисления.
21B116 – AFE16 = x16
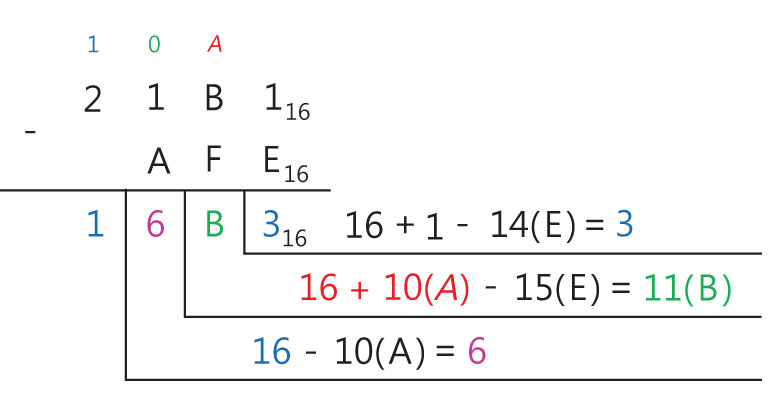
Ответ: 16B316
Пример 25.13. Умножение многозначного числа на однозначное число в троичной системе счисления.
12123 . 23 = x3
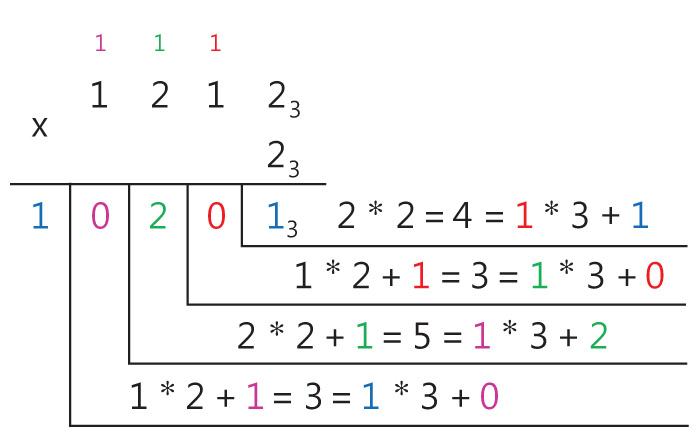
Ответ: 102013
(Пример 25.14. Умножение многозначного числа на однозначное число в восьмеричной системе счисления.
40328 . 78 = x8
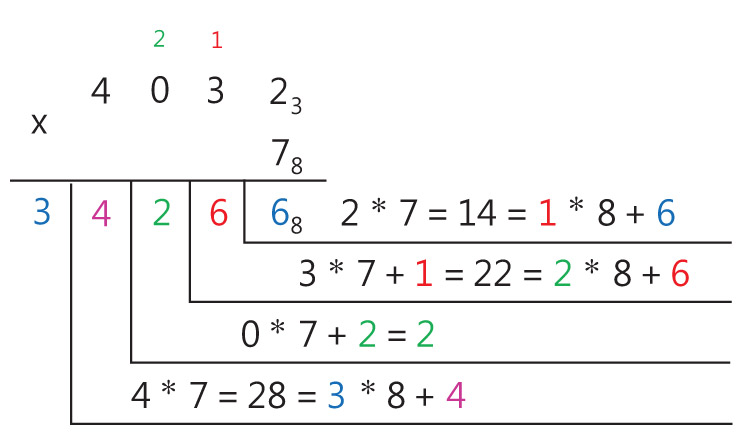
Ответ: 342668
Пример 25.15. Умножение многозначного числа на однозначное число в шестнадцатеричной системе счисления.
623216 . A16 = x16
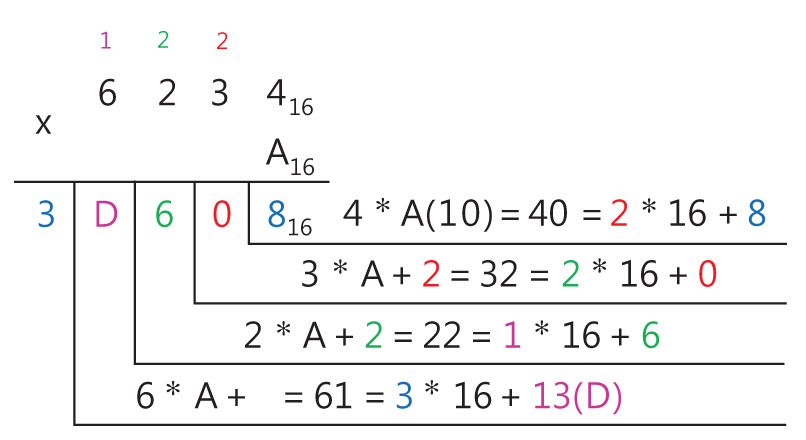
Ответ: 3D60816
Пример 25.16. Умножение чисел в двоичной системе счисления.
101012 . 1012 = x2
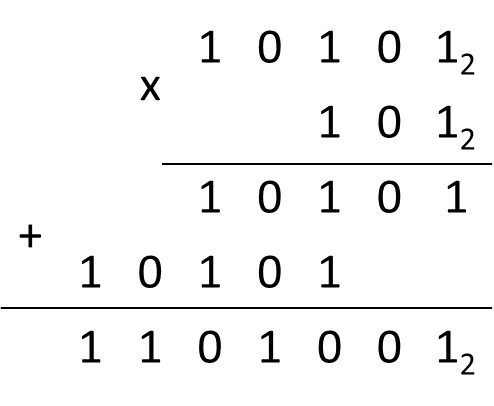
Ответ: 11010012
Пример 25.17. Умножение чисел в пятнадцатеричной системе счисления.
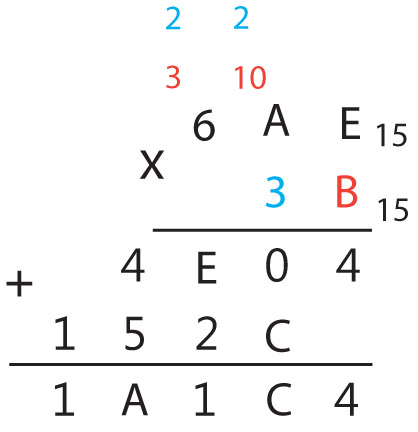
6AE15 . 3B15 = x15
|
Поразрядное умножение на B:
B(11) . E(14) = 154 = 10 . 15 + 4;
B(11) . A(10) + 10 = 120 = 8 . 15 + 0;
B(11) . 6 + 8 = 74 = 4 . 15 + E(14).
Поразрядное умножение на 3:
3 . E(14) = 42 = 2 . 15 + C(12);
3 . A(10) + 2 = 32 = 2 . 15 + 2;
3 . 6 + 2 = 20 = 1 . 15 + 5.
Поразрядное сложение:
4;
0 + C = C;
2 + E(14) = 16 = 1 . 15 + 1;
4 + 5 + 1 = A(10);
1.
|
Ответ: 1A1C415
Пример 25.18. Деление чисел в двоичной системе счисления.
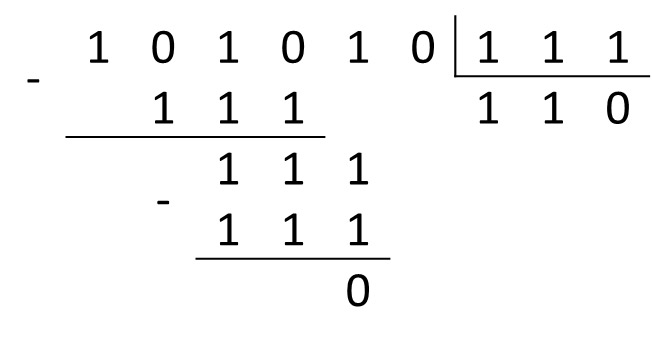
1010102 : 1112 = x2
|
Поразрядное вычитание:
[1]0 – 1 = 1;
[1]0 – 1 = 1;
1 – 1 = 0 – незначащий;
0 – незначащий.
|
Ответ: 1102
Пример 25.19. Деление чисел в восьмеричной системе счисления.
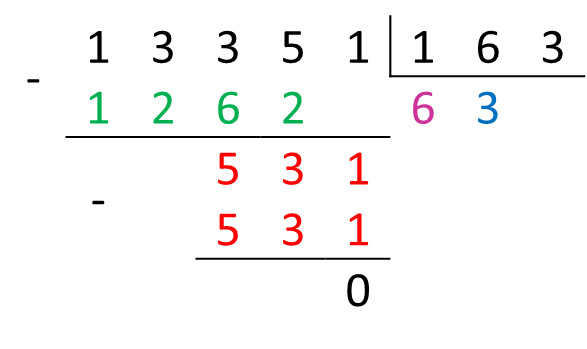
133518 : 1638 = x8
|
Поразрядное умножение на 6:
6 . 3 = 18 = 2 . 8 + 2;
6 . 6 + 2 = 38 = 4 . 8 + 6;
6 . 1 + 4 = 10 = 1 . 8 + 2.
Поразрядное вычитание:
5 – 2 = 3;
8 + 3 = 11; 11 – 6 = 5;
1.
Поразрядное умножение на 3:
3 . 3 = 9 = 1 . 8 + 1;
3 . 6 + 1 = 19 = 2 . 8 + 3;
3 . 1 + 2 = 5.
|
Ответ: 638
Пример 25.20. Деление чисел в шестнадцатеричной системе счисления.
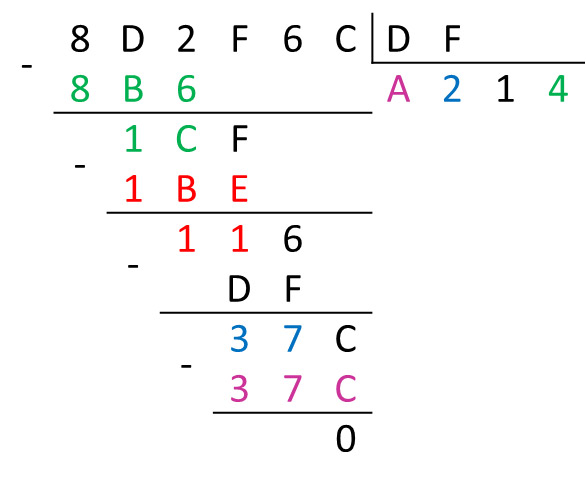
8D2F6C16 : DF16 = x16
|
Поразрядное умножение на A:
A(10) . F(15) = 150 = 9 . 16 + 6;
A(10) . D(13) + 9 = 139 = 8 . 16 + B(11).
Поразрядное вычитание (8D2 – 8B6):
[16]2 – 6 = 16 + 2 – 6 = C(12);
D(13) – 1 – B(11) = 1.
Поразрядное умножение на 2:
2 . F(15) = 30 = 1 . 16 + E(14);
2 . D(13) + 1 = 27 = 1 . 16 + B(11).
Поразрядное вычитание (1CF – 1BE):
F(15) – E(14) = 1;
C(12) – B(11) = 1;
1 – 1 = 0 – незначащий.
Поразрядное вычитание (116 – DF):
[16]6 – F(15) = 16 + 6 – 15 = 7;
[16] – D(13) = 3.
Поразрядное умножение на 4:
4 . F(15) = 60 = 3 . 16 + C(12);
4 . D(13) + 3 = 55 = 3 . 16 + 7.
|
Ответ: A21416
|