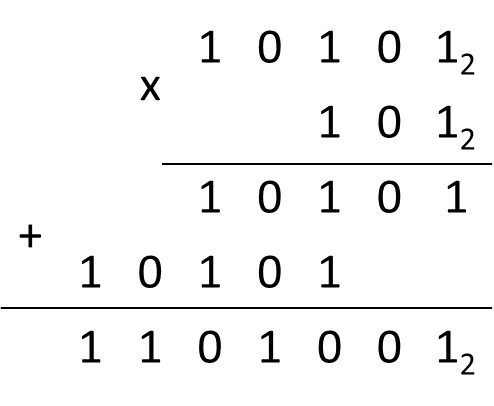§ 25. Кодирование числовых данных

Рассмотрим перевод правильной десятичной дроби в любую другую позиционную систему счисления.

Для перевода десятичной дроби F в систему счисления с основанием q ( F₁₀ → F_q) необходимо F умножить на q, затем дробную часть произведения снова умножить на q и т. д., до тех пор, пока дробная часть произведения не станет равной нулю, либо пока не будет достигнута требуемая точность представления F в системе счисления q (определенное количество цифр в записи результата).

Схема перевода десятичной дроби в двоичную систему счисления выглядит следующим образом:

При повторении значений дробной части (правый столбец таблицы), повторяющуюся группу цифр в записи целых частей (левый столбец таблицы), нужно записать как период дроби.

В примере 25.1 выполнены переводы ( F10 → Fq) десятичных дробей в позиционную систему счисления с основанием q ( F10 → Fq).  

Для смешанных чисел перевод выполняется отдельно для целой и дробной части (пример 25.2).

В ситуации перевода дробей Zp → Zq, когда основания систем счисления (p и q) являются степенями двойки, двоичную систему счисления удобно использовать для перевода как промежуточную по схеме Zp → Z₂ → Zq. В этом случае разделение цифр в записи числа на группы начинается с нулевого разряда и выполняется так же, как и при переводе целых чисел (пример 25.3). При этом разряды в записи чисел нумеруются с 0, и цифра в нулевом разряде соответствует единицам. Нумерация разрядов возрастает влево от нулевого разряда и убывает вправо, т. е. в дробной части числа нумерация разрядов отрицательная.

Алгоритм перевода дробных и смешанных чисел из системы счисления с основанием p в систему счисления с основанием 10 (Zp → Z₁₀ ), так же как для целых чисел, вытекает из способа представления числа в системе счисления с основанием  (пример 25.4).

Правила выполнения арифметических действий (сложения, вычитания, умножения и деления) в десятичной системе счисления хорошо известны. Эти же правила применимы к выполнению арифметических действий и в других позиционных системах счисления.

В примере 25.5 рассмотрены правила выполнения поразрядных арифметических действий в двоичной системе счисления.

Рассмотрим алгоритмы выполнения каждого из арифметических действий в позиционных системах счисления с произвольным основанием .

Сложение

Чтобы в системе счисления с основанием  получить сумму S двух чисел A и B, нужно просуммировать образующие их цифры по разрядам  от младшего разряда к старшему по следующим правилам:

1. Если a_i + b_i < p, то , s_i = a_i + b_i значение (i + 1)-ого разряда не изменяется.
2. Если a_i + b_i ≥ p, то , s_i = a_i + b_i – p, значение ( i + 1)-ого разряда увеличивается на 1. Это связано с тем, что  единиц i-го разряда соответствует одной единице ( i + 1)-го разряда, а в каждом разряде не может находиться более (p – 1) единиц.

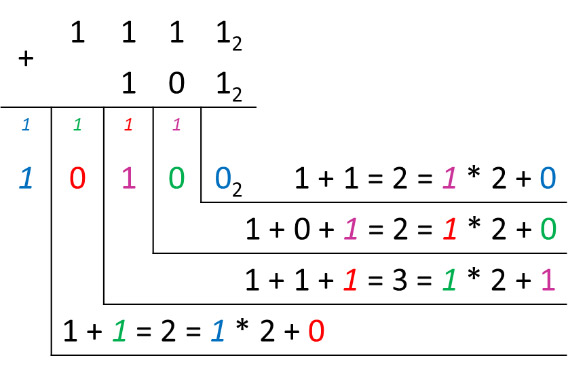
Пример 25.6. Сложить числа 1111₂ и 101₂.

1. Складываем значения в нулевых разрядах слагаемых: 1 + 1 = 10₂. Записываем 0 и 1, переносим в первый разряд.
2. В первых разрядах складываем: 1 + 0 = 1 и добавляем 1 из нулевого разряда. Получаем 1 + 0 + 1 = 10₂. Записываем 0, а 1 переносим во второй разряд.
3. Складываем значения во вторых разрядах: 1 + 1 + 1 = 3(11₂), 3 ≥ 2, значит, записываем 1, и 1 переносим в третий разряд.
4. Вычисляем в третьем разряде: 1 + 1 = 2. Так как 2 ≥ 2, то записываем 0, а 1 переносим в четвертый разряд.

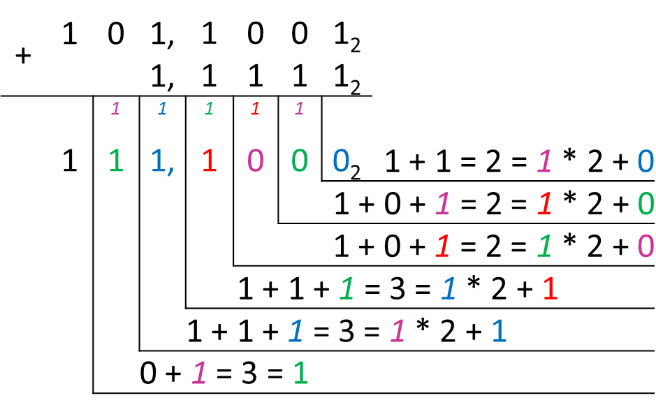
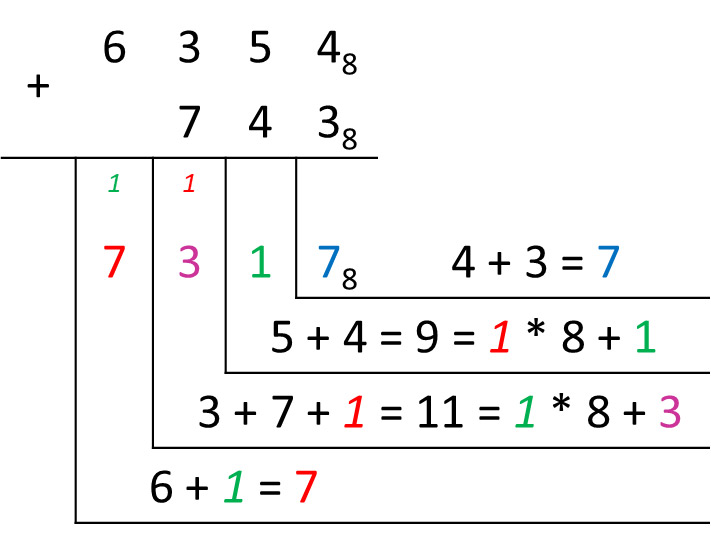
В примере 25.7 выполнено сложение двоичных смешанных чисел.

Пример 25.8. Сложить числа 6354₈ и 743₈.

1. Вычисляем: 4 + 3 = 7.
2. Складываем: 5 + 4 = 9. 9 ≥ 8, значит, записываем 1 (так как 9 – 8 = 1), а 1 переносим во второй разряд.
3. Вычисляем: 3 + 7 = 10. Добавляем 1 из первого разряда 10 + 1 = 11.  11 ≥ 8, значит, записываем 3 (11 – 8 = 3 ), а 1 переносим в третий разряд.
4. В третьем разряде: 6 + 1 = 7.

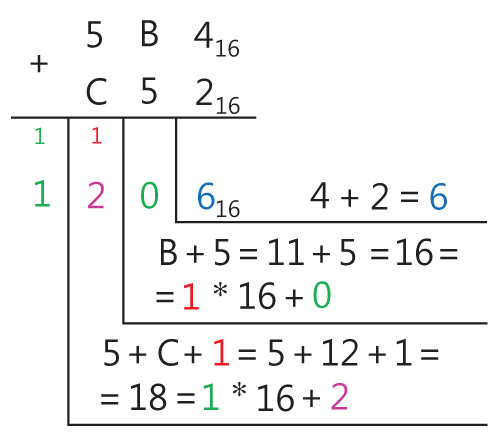
Пример 25.9. Сложить числа 5B4₁₆ и C52₁₆.

1. В нулевом разряде: 4 + 2 = 6.
2. Вычисляем: B(11) + 5 = 16. 16 ≥ 16, значит, записываем 0 (16 – 16 = 0), а 1 переносим во второй разряд.
3. Складываем: 5 + C(12) = 17. Добавляем 1 из второго разряда: 17 + 1 = 18. 18 ≥ 16, значит, записываем 2 (18 – 16 = 2), а 1 переносим в третий разряд.

Вычитание

Чтобы в системе счисления с основанием  получить разность R двух чисел A и B ( A > B), нужно вычислять разности образующих их цифр по разрядам i от младшего к старшему по следующему правилу:

1.  Если  a_i  ≥  b_i, то r_i = a_i – b_i, значение в (i + 1 )-м разряде не изменяется.
2. Если a_i  <  bi, то r_i = p + a_i – b_i, то значение в (i + 1 )-м разряде уменьшается на 1. При этом, если a_i = 0, то занимаем одну разрядную единицу (равную основанию системы счисления p) в (i + 1)-м разряде и продолжаем занимать до ближайшего к i-му старшего разряда (включительно), где a_i ≠ 0.

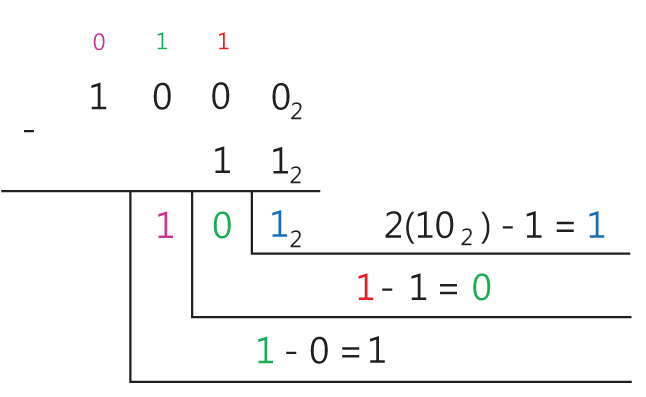
Пример 25.10. Найти разность чисел 1000₂ и 11₂.

1. В нулевом разряде: 0 < 1. Занимаем в первом разряде. Так как в двух следующих разрядах записан 0, то продолжаем занимать до третьего разряда, где записано 1. Получаем 2 – 1 = 1 (10₂ – 1₂ = 1₂). В результат записываем 1.
2. В первом разряде после того, как заняли, осталось 1 (2(10₂) – 1). Вычитаем: 1 – 1 = 0. В результат записываем 0.
3. Во втором разряде осталось 1. Вычитаем: 1 – 0 = 1. В результат записываем 1.
4. В третьем разряде остается 0.

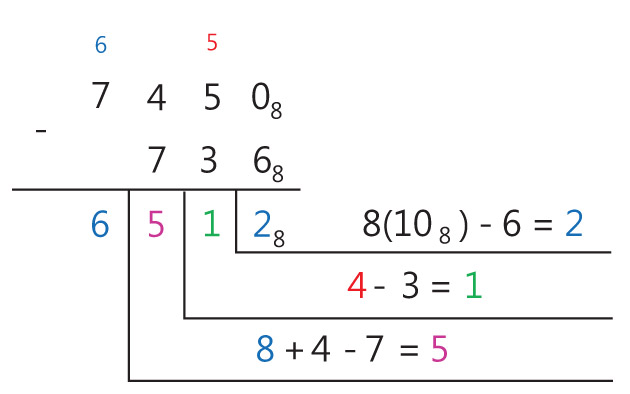
Пример 25.11. Найти разность чисел 7450₈ и 736₈.

1. В нулевом разряде:  0 < 6. Занимаем в первом разряде 8(10₈). Вычитаем: 8 – 6 = 2. В результат записываем 2.
2. В первом разряде осталось 4. Вычитаем: 4 – 3 = 1. В результат записываем 1.
3. Во втором разряде: 4 < 7. Занимаем в третьем разряде 8. Вычисляем: 8 + 4 – 7 = 5. В результат записываем 5.
4. В третьем разряде остается 6, что и записываем в результат.

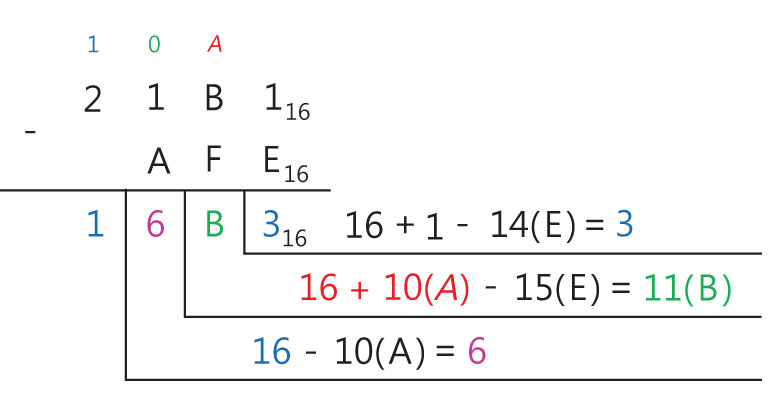
В примере 25.12 рассмотрено вычитание чисел в шестнадцатеричной системе счисления, которое выполняется по аналогичному алгоритму.

Умножение

Чтобы в системе счисления с основанием p получить произведение М числа A и числа  B < p, надо вычислить произведение цифр числа А по разрядам от младшего к старшему и числа В в соответствии с правилами:

1. Если a_i · b < p, то  m_i = a_i · b и значение в (i + 1)-м разряде не изменяется.
2. Если a_i · b < p, то  m_i = ai · b modp, а значение в ( i + 1 )-м разряде увеличивается на a_i · b divp.

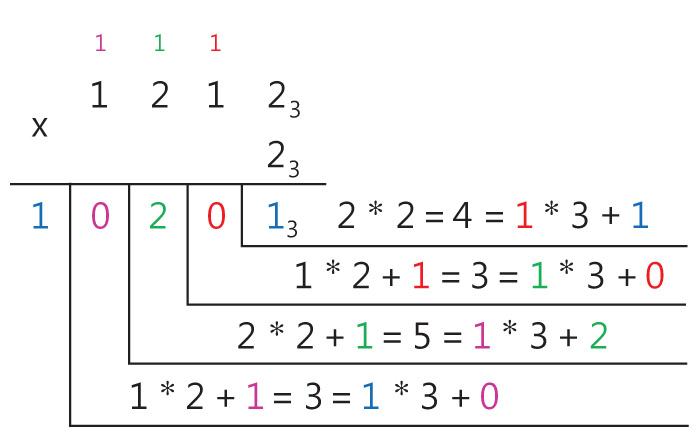
Пример 25.13. Найти произведение чисел 1212₃ и 2₃.

1. Вычисляем: 2 · 2 = 4. Так как 4 ≥ 3, в результат записываем 4 mod 3 = 1. Значение в первом разряде увеличиваем на  4 div 3 = 1.
2. Вычисляем: 1 · 2 + 1 = 3, 3 ≥ 3, значит, в результат записываем 3 mod 3 = 0, а второй разряд увеличиваем на 3 div 3 = 1.
3. Вычисляем: 2 ^.  2 + 1 = 5. В результат записываем 5 mod 3 = 2. Третий разряд увеличиваем на 5 div 3 = 1.
4. Повторяем п. 2. В третьем разряде результата записываем 0, а в четвертом — 1.

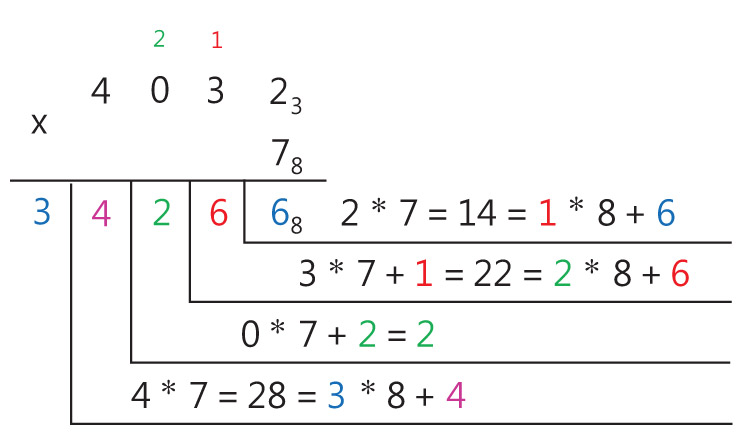
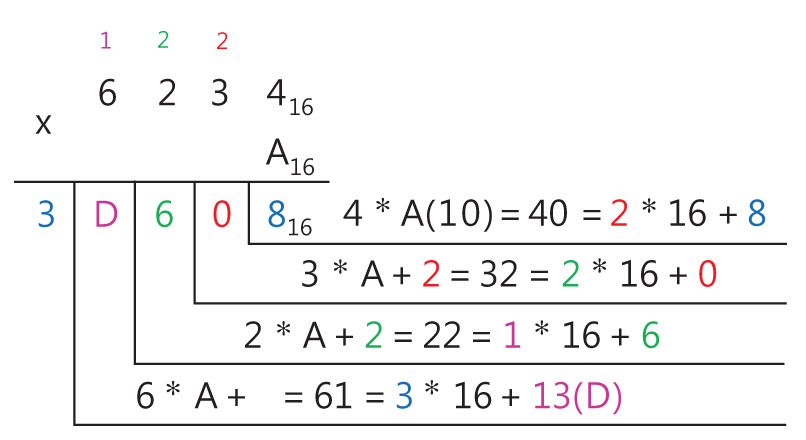
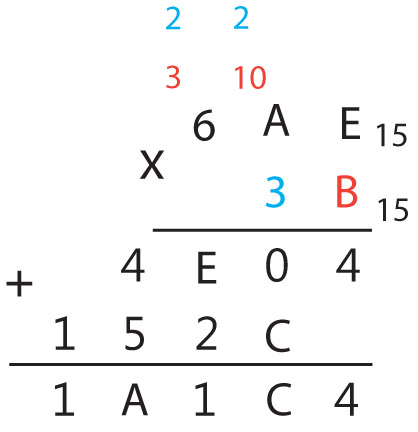
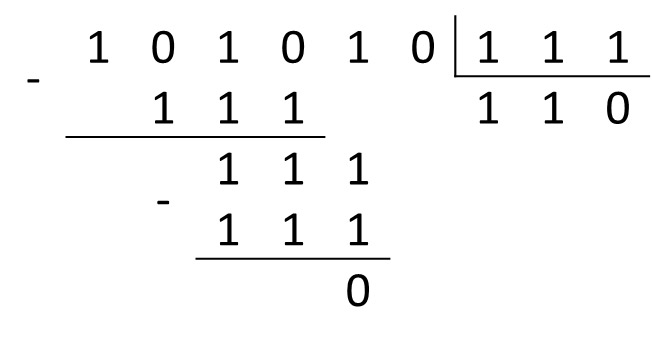
В примерах 25.14 и 25.15 по аналогичному алгоритму выполнено умножение многозначного числа на однозначное число в других системах счисления.

Умножение многозначного числа на многозначное число выполняется столбиком. При этом два множителя располагаются один под другим так, чтобы разряды чисел совпадали (находились в одном столбце).

В примерах 25.16 и 25.17 выполнено умножение многозначного числа на многозначное число.

*Деление

Операцию деления нельзя свести к поразрядным операциям над цифрами, составляющими число. Деление чисел в системе счисления с произвольным основанием  выполняется так же, как и в десятичной системе счисления. А это значит, что при выполнении деления применяются правила умножения и вычитания чисел в системе счисления с основанием p. В отличие от других арифметических действий деление выполняется начиная со старшего разряда делимого.

Пример 25.18. Найти частное чисел 101010₂ и 111₂.

1. Сравниваем значение в самом старшем разряде и делитель. Если делитель больше значения в данном разряде, то рассматриваем это значение и значение в следующем разряде как число. Повторяем операцию до момента, когда полученное число сравняется либо превысит значение делителя ( 1 <  111, 10 < 111, 101 < 111, 1010 > 111).
2. Подбираем такое число (1), при котором произведение делителя и этого числа (111) будет максимально близким по значению (но не больше) к числу, полученному в п. 1. Записываем это число в частное первым.
3. Вычитаем произведение (п. 2) от числа, образованного значениями выбранных разрядов (1010 – 111).
4. Остаток пишем после черты (11).
5. Сносим значение следующего разряда к остатку (1) и проверяем, больше или равно получившееся число (111) делителя. Если нет, то сносим значение еще одного разряда до тех пор, пока не образуется число больше или равное делителя, при этом не забываем записывать нули в частное.
6. Проделываем все вышеперечисленное до тех пор, пока цифры в делимом не закончатся или в остатке не получится число меньше делителя.

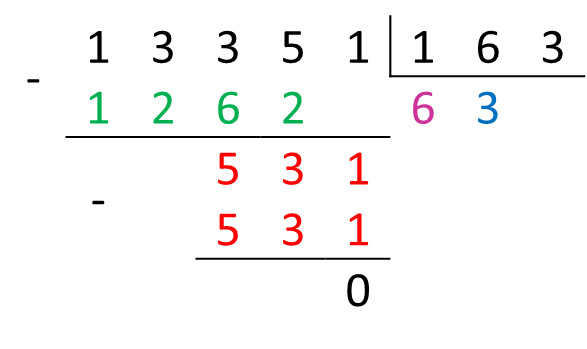
Пример 25.19. Найти частное чисел 13351₈ и 163₈.

1. Сравниваем:1 <  163, 13 < 163, 133 < 163. 1335 > 163.
2. Подбираем: 6 · 163 = 1262 < 1335.
3. Вычитаем: 1335 – 1262 = 53.
4. Сносим 1 и получаем 531 > 163.
5. Подбираем: 3 ^.  163 = 531.
6. Вычитаем: 531 – 531 = 0.

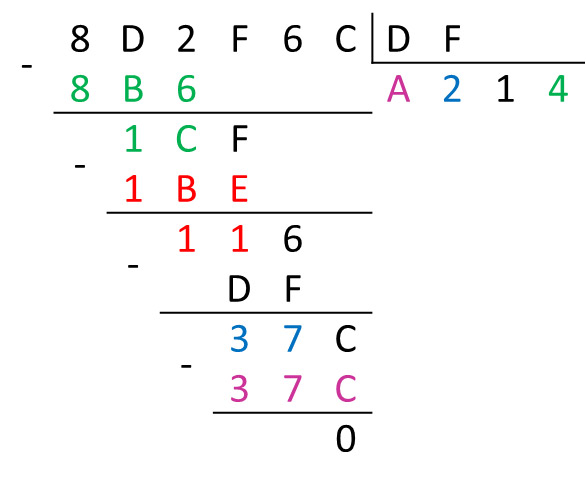
Пример 25.20. Найти частное чисел 8D2F6C₁₆ и DF₁₆.

1. Сравниваем: 8 < DF, 8D < DF, 8D2 > DF.
2. Подбираем: А ^. DF = 8B6 < 8D2.
3. Вычитаем: 8D2 – 8B6 = 1C.
4. Сносим F и получаем 1CF > DF.
5. Подбираем: 2 ^. DF = 1BE < 1CF.
6. Вычитаем: 1CF – 1BE = 11.
7. Сносим 6 и получаем 116 > DF.
8. Подбираем: 1 ^. DF = DF.
9. Вычитаем: 116 – DF = 37.
10. Сносим C и получаем 37C > DF.
11. Подбираем: 4 ^. DF = 37C.
12. Вычитаем: 37C – 37C = 0.

1. Как перевести правильную десятичную дробь в другую систему счисления?

2. Как перевести смешанное число из десятичной системы счисления в любую другую систему счисления?

3. Какой алгоритм используется при переводе смешанного числа из системы счисления с любым основанием в десятичную систему счисления?

4. Каковы правила двоичной арифметики?

5. Как выполняется операция сложения чисел в любой позиционной системе счисления?

6. Как выполняется операция вычитания чисел в любой позиционной системе счисления?

7. Как выполняется операция умножения чисел в любой позиционной системе счисления?

8. Правила выполнения каких арифметических действий используются при выполнении деления в любой позиционной системе счисления?

Система счисления

Количество цифр после запятой.

2^-7

8^-4

16^-3