§ 20. Использование библиотечных функций для сортировки и поиска данных

20.2. Сортировка

Для сортировки элементов вектора используется функция sort, которая имеет два параметра: границы сортируемого диапазона.

Если в качестве границ диапазона использовать стандартные итераторы begin() и end(), то элементы вектора будут отсортированы в порядке возрастания. Если использовать итераторы rbegin() и rend(), то элементы будут отсортированы в порядке убывания. При этом вектор должен состоять из элементов, для которых определены операции сравнения: целых или вещественных чисел, символов, строк.

Если вектор состоит из элементов, для которых не определено понятие порядка (структур или других векторов), то для их сортировки необходим третий параметр — функция-компаратор, которая задает отношения порядка для элементов.

Пример 20.3. Дан линейный массив целых чисел. Написать программу, которая отсортирует числа в порядке убывания.

Этапы выполнения задания

I.  Исходные данные: переменные n — количество чисел в массиве, a — массив.

II.  Результат: отсортированный массив.

III. Алгоритм решения задачи.

1. Ввод исходных данных. Данные сгенерируем случайным образом.
2. Будем использовать функцию sort. Поскольку сортировать элементы нужно по убыванию, то будем использовать обратные итераторы rbegin() и rend().
4. Вывод результата.

IV. Описание переменных: n – int, a –  vector<int>.

Для сортировки в порядке убывания можно воспользоваться стандартным компаратором, который задает порядок — большее раньше меньшего:

sort(v.begin(), v.end(), greater<int>());

Кроме компаратора greater, могут использоваться компараторы: less (меньше), equal_to (равно), not_equal_to (не равно), less_equal (меньше либо равно), greater_equal (больше либо равно). Эти компараторы ассоциированы с типом своего параметра, для которого должны быть определены операции сравнения. По умолчанию работает компаратор less, который можно опускать.

Пример 20.4. На плоскости заданы своими координатами n точек. Расположить точки в порядке возрастания их абсцисс. Найти все пары соседних точек, абсциссы которых находятся на расстоянии не меньше l друг от друга.

Этапы выполнения задания

I. Исходные данные: переменные n — количество точек в массиве, l — расстояние, a — массив.

II.  Результат: отсортированный массив.

III. Алгоритм решения задачи.

1. Ввод исходных данных.
2. Отсортируем точки возрастания их абсцисс с помощью функции sort. Для сравнения точек напишем компаратор.
3. Просмотрим соседние элементы массива и выведем те из них, которые удовлетворяют условию.
4. Вывод результата.

IV. Описание переменных: n, – int, a –  vector<int>.

В реализации Стандартной библиотеки шаблонов (STL) в C++ для реализации сортировки используется подход Дэвида Мюссера. В 1997 г. он предложил использовать интроспективную сортировку (Introsort). Это комбинированный алгоритм сортировки, который использует быструю сортировку и переключается на пирамидальную[1] сортировку, когда глубина рекурсии превысит логарифм от числа сортируемых элементов. В быстрой сортировке выбор опорного элемента производится как медианы из трех. Когда количество элементов становится меньше 16, применяется алгоритм сортировки простыми вставками. Таким образом, функция sort объединяет в себе три алгоритма сортировки: быструю, пирамидальную и сортировку простыми вставками. Функция гарантировано использует порядка  операций сравнений и обменов.

Пример 20.3.

V. Программа:

#include <iostream>

#include <vector>

#include <cstdlib>

#include <ctime>

#include <algorithm>

 

using namespace std;

 

int main()

{

  srand(time(NULL));

  int n;

  cout << "n = ";

  cin >> n;

  vector <int> a(n);

  cout << "chisla:" << endl;

  for (int i = 0; i < n; i++){

    a[i] = rand() % 100;

    cout << a[i] << " ";

  }

  cout << endl << "sort" << endl;

  sort(a.rbegin(), a.rend());

  for (int i = 0; i < n; i++)

    cout << a[i] << " ";

  cout << endl;

  return 0;

}

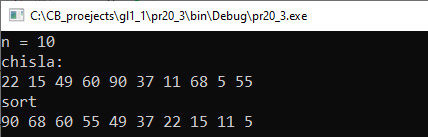
VI.  Тестирование.

Пример 20.4.

V. Программа:

#include <iostream>

#include <cmath>

#include <vector>

#include <algorithm>

 

using namespace std;

 

struct tchk

{

  double x, y;

};

 

bool comp(tchk a, tchk b)

{

  return (a.x < b.x ||

      (a.x == b.x && a.y < b.y));

}

 

int main()

{

  int n;

  cout << "n = ";

  cin >> n;

  vector <tchk> t(n);

  cout << "koordinaty tochek" << endl;

  for (int i = 0; i<n; i++)

    cin >> t[i].x >> t[i].y;

  /// сортировка

  sort(t.begin(), t.end(), comp);

  cout << "sort" << endl;

  for (int i = 0; i < n; i++)

    cout << "(" << t[i].x << "," 

        << t[i].y << ")" << " ";

  cout << endl;

  double l;

  cout << "l = ";

  cin >> l;

  ///поиск

  for (int i = 0; i < n - 1; i++)

    if (abs(t[i].x - t[i + 1].x) >= l){

      cout << "(" << t[i].x << ",";

      cout << t[i].y << ")" << '\t';

      cout << "(" << t[i + 1].x ;

      cout << ","<< t[i + 1].y;

      cout << ")" << endl;

    }

  return 0;

}

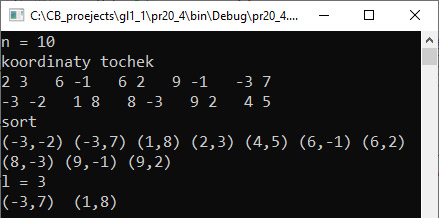
VI. Тестирование.


[1] Пирамидальная сортировка использует бинарное сортирующее дерево для хранения данных. Почитать о ней можно здесь: Кормен, Т. Алгоритмы: построение и анализ / Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн., 3-е издание. — М.: «Вильямс», 2013.