Печатать книгуПечатать книгу

§ 20. Использование библиотечных функций для сортировки и поиска данных

Сайт: Профильное обучение
Курс: Информатика. 10 класс (Повышенный уровень)
Книга: § 20. Использование библиотечных функций для сортировки и поиска данных
Напечатано:: Гость
Дата: Суббота, 21 Декабрь 2024, 16:00

Оглавление

Многие из рассмотренных нами задач достаточно часто встречаются на практике. Поэтому их решения, оформленные в виде соответствующих функций, были включены в библиотеку algorithm[1]. Для подключения библиотеки необходима команда #include <algorithm>.

Рассмотрим некоторые из функций этой библиотеки. В Приложении можно найти более подробный список.


[1] https://ru.cppreference.com/w/cpp/algorithm (дата доступа 25.06.2020).

20.1. Линейный поиск элемента

Для организации линейного поиска элемента в массиве можно использовать следующие функции:

find

Находит значение в данном диапазоне

count

Возвращает количество элементов, соответствующее данному значению

find_if

Ищет первое вхождение элемента, для которого верно значение функции компаратора

count_if

Возвращает количество элементов, для которых значение функции компаратора является истиной

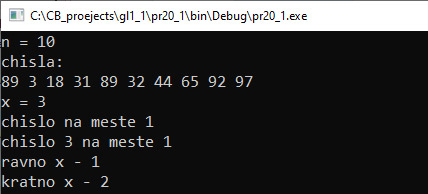
У всех этих функций три параметра. Первые два параметра являются итераторами, которые определяют диапазон для поиска в массиве, третий задает условие поиска. При этом левая граница диапазона входит в область поиска, а правая — нет. То есть диапазон поиска является полуинтервалом. Если поиск осуществляется во всем векторе, то используются итераторы begin() и end().

В качестве результата функции find и find_if выдают значение итератора, указывающего на первый элемент, соответствующий поисковому запросу.

Компаратор для функций, реализующих поиск элемента в диапазоне, имеет один параметр. Компаратор возвращает значение true, если элемент удовлетворяет условию поиска, и false, если нет. Функция поиска передает в компаратор поочередно значения из диапазона поиска. Как только для какого-то значения получили true, работа поисковой функции прекращается.

Если элемент не найден, функция возвращает итератор на правую границу области поиска.

Пример 20.1. Дан линейный массив целых чисел. Написать программу, которая:

1) найдет позицию элемента, равного x;

2) найдет позицию элемента, кратного x;

3) посчитает количество элементов, равных x;

4) посчитает количество элементов, кратных x.

Этапы выполнения задания

 I. Исходные данные: переменные n — количество чисел в массиве, a — массив.

II. Результат: позиции элементов n1 и n2 (пункты 1 и 2) и количество элементов k1 и k2 (пункты 3 и 4).

III. Алгоритм решения задачи.

1. Ввод исходных данных. Данные сгенерируем случайным образом.
2. Будем использовать следующие функции:

2.1. find для пункта 1.
2.2. find_if для пункта 2.
2.3. count для пункта 3.
2.4. count_if для пункта 4.

3. Вывод результата.

IV. Описание переменных: n, k1, k2, n1, n2, x – int, a –  vector<int>.

Функции min_element и max_element возвращают итератор на минимальное и максимальное значения элементов в диапазоне.

Пример 20.2. Дан линейный массив целых чисел. Написать программу, которая найдет минимальный и максимальный элементы в массиве.

Этапы выполнения задания

I. Исходные данные: переменные n — количество чисел в массиве, a — массив.

II. Результат: позиции минимального и максимального элементов nmin и nmax и их значения.

III. Алгоритм решения задачи.

1. Ввод исходных данных. Данные сгенерируем случайным образом.
2. Будем использовать соответствующие функции.
3. Вывод результата.

IV. Описание переменных: n, n1, n2 – int, a –  vector<int>.

Пример 20.1.

V. Программа:

#include <iostream>

#include <vector>

#include <algorithm>

#include <cstdlib>

#include <ctime>

 

using namespace std;

 

int x;

 

bool comp(int t)

{

  return (t % x == 0);

}

 

int main()

{

  srand(time(NULL));

  int n;

  cout << "n = ";

  cin >> n;

  vector<int> a(n);

  cout << "chisla:" << endl;

  for (int i = 0; i < n; i++){

    a[i] = rand() % 100;

    cout << a[i] << " ";

  }

  cout<<endl;

//поиск элемента x в массиве

  cout << "x = ";

  cin >> x;

  int n1 = find(a.begin(), a.end(), x) - a.begin();

  if(n1 < a.size())

    cout << "chislo na meste " << n1 << endl;

  else

    cout << "net chisla = x" << endl;

//поиск по условию: число кратно x

  int n2 = find_if(a.begin(), a.end(), comp) - a.begin();

  if (n2 < a.size()){

    cout << "chislo " << a[n2];

    cout << " na meste " << n2;

    cout << endl;

  }

  else

    cout << "net kratnyh chisel" << endl;

//количество элементов, равных х

  int k1 = count(a.begin(), a.end(), x);

  cout << "ravno x - " << k1 << endl;

//количество элементов, кратных х

  int k2 = count_if(a.begin(), a.end(), comp);

  cout << "kratno x - " << k2 << endl;

  return 0;

}

 VI. Тестирование.

Анализ результатов. Индекс числа 3 в массиве равен 1, а также это число кратно самому себе. В массиве одно число, равное 3, и два числа (3 и 18), кратных 3.

Обратите внимание на то, что переменная x описана как глобальная переменная, поскольку она используется как в функции main, так и в компараторе comp.

Пример 20.2.

 V. Программа:

#include <iostream>

#include <vector>

#include <algorithm>

#include <cstdlib>

#include <ctime>

 

using namespace std;

 

int main()

{

  srand(time(NULL));

  int n;

  cout << "n = ";

  cin >> n;

  vector<int> a(n);

  cout << "chisla:" << endl;

  for (int i = 0; i < n; i++){

    a[i] = rand() % 100;

    cout << a[i] << " ";

  }

  cout<<endl;

  //поиск минимального и 

  //максимального

  int nmin = min_element(a.begin(), a.end()) - a.begin();

  cout << "min element = " << a[nmin];

  cout << " na meste - " << nmin << endl;

  int nmax = max_element(a.begin(), a.end()) - a.begin();

  cout << "max element = " << a[nmax];

  cout << " na meste - " << nmax << endl;

  return 0;

}

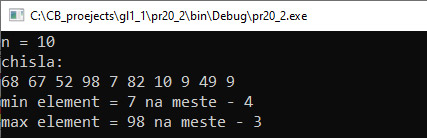
 VI. Тестирование.

Функции  min_element  и  max_element   могут иметь третий параметр — компаратор, определяющий правило порядка для элементов указанного диапазона.

20.2. Сортировка

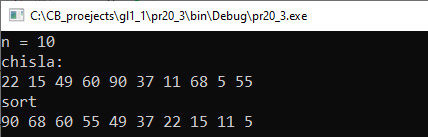
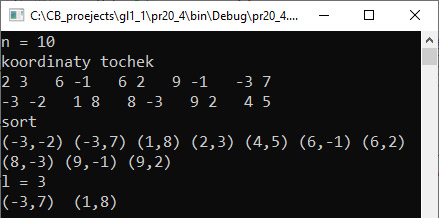
Для сортировки элементов вектора используется функция sort, которая имеет два параметра: границы сортируемого диапазона.

Если в качестве границ диапазона использовать стандартные итераторы begin() и end(), то элементы вектора будут отсортированы в порядке возрастания. Если использовать итераторы rbegin() и rend(), то элементы будут отсортированы в порядке убывания. При этом вектор должен состоять из элементов, для которых определены операции сравнения: целых или вещественных чисел, символов, строк.

Если вектор состоит из элементов, для которых не определено понятие порядка (структур или других векторов), то для их сортировки необходим третий параметр — функция-компаратор, которая задает отношения порядка для элементов.

Пример 20.3. Дан линейный массив целых чисел. Написать программу, которая отсортирует числа в порядке убывания.

Этапы выполнения задания

I.  Исходные данные: переменные n — количество чисел в массиве, a — массив.

II.  Результат: отсортированный массив.

III. Алгоритм решения задачи.

1. Ввод исходных данных. Данные сгенерируем случайным образом.
2. Будем использовать функцию sort. Поскольку сортировать элементы нужно по убыванию, то будем использовать обратные итераторы rbegin() и rend().
4. Вывод результата.

IV. Описание переменных: n – int, a –  vector<int>.

Для сортировки в порядке убывания можно воспользоваться стандартным компаратором, который задает порядок — большее раньше меньшего:

sort(v.begin(), v.end(), greater<int>());

Кроме компаратора greater, могут использоваться компараторы: less (меньше), equal_to (равно), not_equal_to (не равно), less_equal (меньше либо равно), greater_equal (больше либо равно). Эти компараторы ассоциированы с типом своего параметра, для которого должны быть определены операции сравнения. По умолчанию работает компаратор less, который можно опускать.

Пример 20.4. На плоскости заданы своими координатами n точек. Расположить точки в порядке возрастания их абсцисс. Найти все пары соседних точек, абсциссы которых находятся на расстоянии не меньше l друг от друга.

Этапы выполнения задания

I. Исходные данные: переменные n — количество точек в массиве, l — расстояние, a — массив.

II.  Результат: отсортированный массив.

III. Алгоритм решения задачи.

1. Ввод исходных данных.
2. Отсортируем точки возрастания их абсцисс с помощью функции sort. Для сравнения точек напишем компаратор.
3. Просмотрим соседние элементы массива и выведем те из них, которые удовлетворяют условию.
4. Вывод результата.

IV. Описание переменных: n, – int, a –  vector<int>.

В реализации Стандартной библиотеки шаблонов (STL) в C++ для реализации сортировки используется подход Дэвида Мюссера. В 1997 г. он предложил использовать интроспективную сортировку (Introsort). Это комбинированный алгоритм сортировки, который использует быструю сортировку и переключается на пирамидальную[1] сортировку, когда глубина рекурсии превысит логарифм от числа сортируемых элементов. В быстрой сортировке выбор опорного элемента производится как медианы из трех. Когда количество элементов становится меньше 16, применяется алгоритм сортировки простыми вставками. Таким образом, функция sort объединяет в себе три алгоритма сортировки: быструю, пирамидальную и сортировку простыми вставками. Функция гарантировано использует порядка  операций сравнений и обменов.

Пример 20.3.

V. Программа:

#include <iostream>

#include <vector>

#include <cstdlib>

#include <ctime>

#include <algorithm>

 

using namespace std;

 

int main()

{

  srand(time(NULL));

  int n;

  cout << "n = ";

  cin >> n;

  vector <int> a(n);

  cout << "chisla:" << endl;

  for (int i = 0; i < n; i++){

    a[i] = rand() % 100;

    cout << a[i] << " ";

  }

  cout << endl << "sort" << endl;

  sort(a.rbegin(), a.rend());

  for (int i = 0; i < n; i++)

    cout << a[i] << " ";

  cout << endl;

  return 0;

}

VI.  Тестирование.

Пример 20.4.

V. Программа:

#include <iostream>

#include <cmath>

#include <vector>

#include <algorithm>

 

using namespace std;

 

struct tchk

{

  double x, y;

};

 

bool comp(tchk a, tchk b)

{

  return (a.x < b.x ||

      (a.x == b.x && a.y < b.y));

}

 

int main()

{

  int n;

  cout << "n = ";

  cin >> n;

  vector <tchk> t(n);

  cout << "koordinaty tochek" << endl;

  for (int i = 0; i<n; i++)

    cin >> t[i].x >> t[i].y;

  /// сортировка

  sort(t.begin(), t.end(), comp);

  cout << "sort" << endl;

  for (int i = 0; i < n; i++)

    cout << "(" << t[i].x << "," 

        << t[i].y << ")" << " ";

  cout << endl;

  double l;

  cout << "l = ";

  cin >> l;

  ///поиск

  for (int i = 0; i < n - 1; i++)

    if (abs(t[i].x - t[i + 1].x) >= l){

      cout << "(" << t[i].x << ",";

      cout << t[i].y << ")" << '\t';

      cout << "(" << t[i + 1].x ;

      cout << ","<< t[i + 1].y;

      cout << ")" << endl;

    }

  return 0;

}

VI. Тестирование.


[1] Пирамидальная сортировка использует бинарное сортирующее дерево для хранения данных. Почитать о ней можно здесь: Кормен, Т. Алгоритмы: построение и анализ / Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн., 3-е издание. — М.: «Вильямс», 2013.

20.3. Бинарный поиск

Если массив отсортирован, то для поиска элемента x можно применять алгоритм бинарного поиска. Алгоритм дихотомии реализован в нескольких функциях:

binary_search

Определяет, присутствует ли элемент в некотором диапазоне

equal_range

Ищет диапазон элементов, равных определенному элементу

lower_bound

Ищет первое место в диапазоне, в которое можно вставить значение, сохраняя упорядоченность

upper_bound

Ищет последнее место, куда можно вставить значения, сохраняя упорядоченность (первое место, в котором элемент больше, чем вставляемое значение)

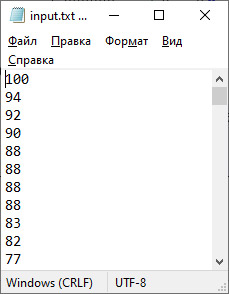
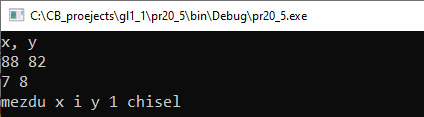
В качестве параметров задаются итераторы, указывающие диапазон поиска и искомое значение. Функции могут иметь четвертый параметр — компаратор, указывающий на порядок сортировки элементов в массиве.

Пример 20.5. Дан линейный отсортированный массив целых чисел. Написать программу, которая получит количество элементов, меньших x и больших y. Массив упорядочен в порядке убывания. Данные прочитать из файла. Числа x и y ввести с клавиатуры.

Этапы выполнения задания

I. Исходные данные: переменные n –количество чисел в массиве, a — массив, числа x и y.

II. Результат: количество элементов, меньших x и больших y.

III. Алгоритм решения задачи.

1. Ввод исходных данных.
2. Для решения задачи будем использовать алгоритм бинарного поиска.

2.1. Для поиска n1 — номера первого значения, меньшего x, воспользуемся функцией upper_bound. 
2.2. Для поиска n2 — номера первого значения, большего y, воспользуемся функцией lower_bound. 
2.3. Ответом будет значение, равное модулю разности позиций для чисел x и y. 
2.4. Вывод результата.

IV. Описание переменных: n, n1, n2, x, y – int, a –  vector<int>.

Функция  equal_range  возвращает диапазон, содержащий все элементы, равные x. Диапазон определяется двумя итераторами, первый указывает на первый элемент, не меньший (равный или больше), чем x, второй указывает на первый элемент, больший, чем x. Первый итератор может быть получен использованием  lower_bound(),  второй —   upper_bound().  Возвращаемым значением является тип пара (pair), содержащий два итератора.

Для использования типа данных  pair  необходима библиотека  utility. 

Пример 20.5.

V. Программа:

#include <iostream>

#include <fstream>

#include <vector>

#include <cmath>

#include <algorithm>

 

using namespace std;

 

int main()

{

  ifstream fin("input.txt");

  int n;

  fin >> n;

  vector <int> a(n);

  for (int i = 0; i < n; i++)

    fin >> a[i];

  int x, y;

  cout << "x, y" << endl;

  cin >> x >> y;

  int n1 = upper_bound(

          a.begin(), a.end(),

          x, greater<int>())

          - a.begin();

  int n2 = lower_bound(

          a.begin(), a.end(),

          y, greater<int>())

          - a.begin();

  cout << n1 << " " << n2 << endl;

  int rez = abs(n2 - n1);

  cout << "mezdu x i y ";

  cout << rez << " chisel";

  cout << endl;

  return 0;

}

 VI. Тестирование.

 

 

Анализ результатов. Значение 7 – номер первого меньшего 88, а значение 8 — номер первого большего 82.

Вопросы к параграфу

1. Какую библиотеку можно использовать для поиска и сортировки элементов массива?

2. Какие функции позволяют осуществлять поиск элемента?

3. С помощью какой функции можно отсортировать массив?

4. В каких функциях реализован алгоритм бинарного поиска?

Упражнения

    

1. Реализуйте решение задач из упражнений 5—7 после § 12, используя функции поиска из библиотеки algorithm.

2. Используя функции для поиска минимального и максимального элементов, реализуйте решение задач из упражнений 6—7, 9—16 после § 13.

3. Отсортируйте массивы из упражнений 3—5 после § 18, используя функцию sort.

4. Используя функции бинарного поиска из библиотеки algorithm, реализуйте решения задач из упражнений 1—2 после § 19.

5. На плоскости своими координатами заданы n точек. Расположить точки в порядке убывания их абсцисс. Найти все тройки соседних точек, абсциссы которых строго убывают.

6*. На плоскости своими координатами заданы n точек. Расположить точки в порядке возрастания угла наклона вектора, заданного данной точкой (угол между вектором и ось ОХ). Если углы равны (отличаются не более чем на 0.00001), то сортировать по длине вектора. Найти величину максимального угла между соседними векторами.