§ 18. Сортировка одномерного массива

18.2. Сортировка выбором

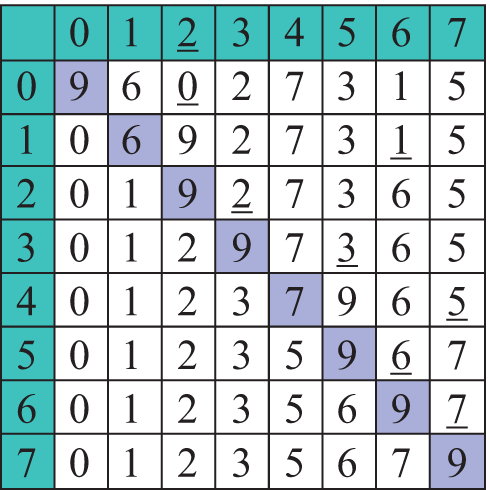
Давайте представим, что перед нами поставлена задача расставить N  чисел по возрастанию. Как бы мы ее решали?

Наверное, пришлось бы сначала найти минимальное из всех чисел и поставить его на первое место в последовательности. Затем из еще неотсортированных элементов надо было бы опять выбрать минимальный элемент и поставить его после уже отсортированной части и т. д. (пример 18.3)

Рассмотрим работу данного метода на массиве a = {9, 6, 0, 2, 7, 3, 1, 5}. Минимальный элемент на каждом шаге подчеркнут (пример 18.4). Цветом выделен тот элемент, который на текущем шаге меняется местами с минимальным.

Примененный метод называется сортировкой выбором. Название метода определяется тем, что на каждом шаге мы находим (выбираем) минимальный элемент из еще неотсортированной части массива (пример 18.5).

Формальное описание алгоритма. На i-м шаге (i = 0, …, n - 1) выполняем:

1. Выбираем из элементов с индексами от i до n–1 минимальный.
2. Меняем местами найденный минимальный элемент и элемент a[i]. На i-м месте оказывается минимальный элемент из еще неотсортированной части массива.
3. После выполнения последнего шага в позиции a[n–1] будет находиться самый большой элемент массива.

Посчитаем количество сравнений, которые пришлось сделать для упорядочения массива. На первом шаге для нахождения максимального элемента необходимо (n – 1) сравнений, на втором — (n – 2), на третьем (n – 3), ..., на последнем шаге — одно сравнение. Найдем сумму: n – 1 + n – 2 + n – 3  ... + 1 = fraction numerator straight n open parentheses straight n space minus space 1 close parentheses over denominator 2 end fraction space equals space fraction numerator straight n squared space minus space straight n over denominator 2 end fraction. Или, другими словами порядка n2 операций[1].

Количество перестановок элементов равно (n – 1). Это количество определятся внешним циклом for.

[1] Более подробно о количестве операций, необходимых для выполнения алгоритмов, см. в § 23.

Пример 18.3. Демонстрация сортировки чисел на примере детской игрушки, в которой нужно выбирать и расставлять числа по своим местам:

Пример 18.4. Сортировка массива методом выбора:

Пример 18.5. Программа алгоритма сортировки методом выбора:

#include <iostream>

#include <vector>

#include <cstdlib>

#include <ctime>

 

using namespace std;

 

int main()

{

  srand(time(NULL));

  int n;

  cout << "n = ";

  cin >> n;

  vector <int> a(n);

  cout << "chisla:" << endl;

  for (int i = 0; i < n; i++){

    a[i] = rand() % 100;

    cout << a[i] << " ";

  }

  cout << endl << "sort" << endl;

  for (int k = 0; k < n - 1; k++){

    int nmin = k;

    for (int i = k + 1; i < n; i++)

      if (a[i] < a[nmin])

       nmin = i;

    swap(a[k], a[nmin]);

  }

  for (int i = 0; i < n; i++)

    cout << a[i] << " ";

  cout << endl;

  return 0;

}

Тестирование.

Внутренний цикл for является не чем иным, как алгоритмом поиска минимального элемента среди элементов с номерами от k + 1 до n – 1.

Сумму количества сравнений можно получить исходя из того, что числа n – 1, n – 2, … 1 образуют арифметическую прогрессию. Сумма элементов этой арифметической прогрессии равна  fraction numerator straight n open parentheses straight n space – space 1 close parentheses over denominator 2 end fraction.