§ 16. Тип данных структура (struct)
16.2. Использование структур для описания геометрических объектов
|
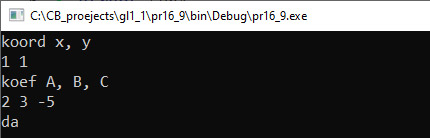
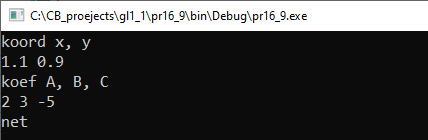
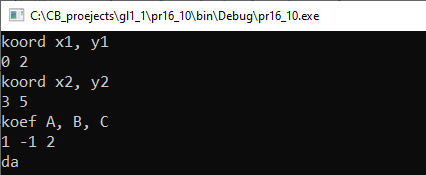
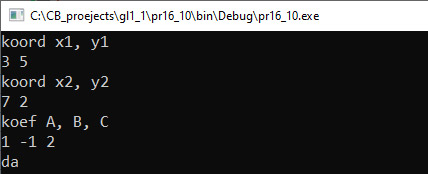
Простейшим геометрическим объектом на плоскости является точка, которая задается своими координатами. Точка описана в примере 16.1. Пара точек на плоскости определяет отрезок, который описан в примере 16.5. Еще одним важным геометрическим объектом на плоскости является прямая. В математике используют разные способы описать прямую с помощью уравнений. Уравнение прямой на плоскости в прямоугольной системе координат — это некоторое уравнение с двумя переменными x и y, которое обращается в тождество при подстановке в него координат любой точки этой прямой. Любая форма уравнения прямой имеет параметры. Используя параметры уравнения, можно описать соответствующую структуру (пример 16.7). Разные формы уравнения прямой (в большинстве случаев) могут быть приведены друг к другу, поскольку они описывают один и тот же объект. Использование той или иной формы уравнения прямой зависит от задачи. Уравнение прямой в общем виде является наиболее универсальным. Любая другая форма уравнения прямой всегда может быть приведена к общему уравнению прямой. Пример 16.8. Известны координаты двух точек, через которые проходит прямая. Получить запись уравнения этой прямой в общем виде. Этапы выполнения задания I. Исходные данные: переменная p1 (структура, описывающая уравнение прямой, проходящей через две точки). II. Результат: переменная p2 (структура, описывающая уравнение прямой в общем виде). III. Алгоритм решения задачи. 1. Ввод исходных данных. Вводим координаты двух точек и создаем из них структуру p1. 4. Вывод результата. IV. Описание переменных: p1, p2 – struct. Пример 16.9. Известны координаты точки и коэффициенты уравнения прямой в общем виде. Определить, принадлежит ли точка прямой. Этапы выполнения задания I. Исходные данные: переменная АВ (структура, описывающая уравнение прямой в общем виде), А (структура, описывающая точку). II. Результат: сообщение «да» или «нет». III. Алгоритм решения задачи. 1. Ввод исходных данных. IV. Описание переменных: A, AB – struct. Пример 16.10. Известны координаты концов отрезка и коэффициенты уравнения прямой в общем виде. Определить, имеют ли прямая и отрезок общие точки. Этапы выполнения задания I. Исходные данные: переменная CD (структура, описывающая уравнение прямой в общем виде), АB (структура, описывающая отрезок). II. Результат: сообщение «да» или «нет». III. Алгоритм решения задачи. 1. Ввод исходных данных. Структуру AB создаем по введенным координатам двух точек. 2. Для того чтобы проверить, имеют ли прямая и отрезок общие точки, создадим функцию otr_na_pr. 3. Отрезок имеет с прямой общие точки, если выполняется одно из условий: 3.1. Один из концов отрезка лежит на прямой. 4. Если точка лежит на прямой, то при подстановке ее координат в уравнение, в левой части общего уравнения прямой получаем 0. Если точка не принадлежит прямой, то получаем одно из двух неравенств: 5. Поскольку вычисления проходят в вещественных числах, то будем проверять, что полученное значение по модулю меньше, чем 10-6. Такой точности на практике обычно бывает достаточно. 6. Вывод результата. IV. Описание переменных: CD, AB – struct. Пример 16.11. Многоугольник задан списком своих вершин в порядке обхода. Для каждой вершины известны ее координаты на плоскости. Найти периметр многоугольника. Этапы выполнения задания I. Исходные данные: n — количество точек, a — массив точек. II. Результат: периметр многоугольника. III. Алгоритм решения задачи. 1. Ввод исходных данных. Создаем массив из точек и вводим координаты. |
Пример 16.7. Формы записи уравнения прямой и соответствующие им описания структур. Уравнение прямой с угловым коэффициентом: y = kx + l. Уравнение не позволяет описать прямую, параллельную оси OY.
Уравнение прямой в отрезках:
Уравнение прямой, проходящей через две точки
Общее уравнение прямой:
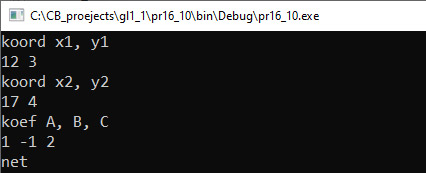
Пример 16.8. V. Программа:
VI. Тестирование. Пример 16.9. V. Программа:
VI. Тестирование.
Пример 16.10. V. Программа:
VI. Тестирование. Отрезок целиком лежит на прямой. Один конец отрезка лежит на прямой. Прямая пересекает отрезок. Нет общих точек. Пример 16.11. V. Программа:
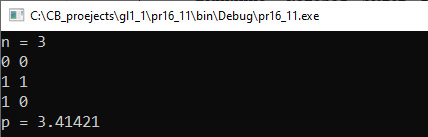
VI. Тестирование. |