Печатать книгуПечатать книгу

§ 16. Тип данных структура (struct)

Сайт: Профильное обучение
Курс: Информатика. 10 класс (Повышенный уровень)
Книга: § 16. Тип данных структура (struct)
Напечатано:: Гость
Дата: Четверг, 28 Ноябрь 2024, 05:43

Оглавление

16.1. Описание структур

Примером структуры может послужить любой объект, который определяется набором своих характеристик. Например, точка на плоскости определяется абсциссой и ординатой, дата — днем, месяцем и годом, для книги такими характеристиками могут быть: автор, название, год издания, количество страниц и т. д. Для описания таких объектов на языке программирования С++ используется ключевое слово struct (структура).

Структура представляет собой сложный тип данных, составленный из простых типов, позволяющий использовать группу связанных между собой данных как единое целое. Отдельный элемент структуры называют полем.

Общая форма объявления структуры:

struct имя_типа

{

  тип_1  элемент_1;

  тип_2  элемент_2;

…

  тип_n  элемент_n;

};

Описывается структура до функции main. После закрывающей фигурной скобки «}» в объявлении структуры обязательно ставится точка с запятой.

В примере 16.1 приведено описание структур. Описание структуры создает новый тип данных. Для того чтобы использовать структуру, нужно описать переменную соответствующего типа (пример 16.2).

Инициализировать структуру можно, присвоив ее переменным значения с помощью синтаксиса инициализации  (аналогично инициализации массивов): в фигурных скобках передаются значения для элементов структуры в том порядке, в котором они описаны (пример 16.3).

Для структур определена единственная операция — присваивание. Все остальные действия при обработке структур происходят с ее полями. Обращение к полю структуры происходит через точку «.» (пример 16.4). С полями структуры можно выполнять все  действия, определенные для типа, которым описано поле.

В качестве поля структуры может быть использована другая структура. Она должна быть описана до того, как используется (пример 16.5). При использовании структур среда программирования выводит подсказку со списком всех полей структуры после того, как пользователь поставит точку. Имя поля можно выбрать из списка (пример 16.6).

Структуры могут передаваться в функции как параметры. Функция может возвращать значение в виде структуры.

Пример 16.1. Описание структур.

Структура для описания точки на плоскости:

struct tchk

{

  double x, y;

};

 Структура для описания даты:

struct date

{

  int d, m, g;

};

Структура для описания книги:

struct kniga

{

  string avt, nazv;

  int str, god;

};

Структура, описывающая студента, поступившего в ВУЗ по результатам ЦТ:

struct student

{

  string fam, gorod;

  int god_r;

  vector <int> otm = vector<int>(3);

  int sr_bal;

};

В данном примере для каждого студента хранится его фамилия (fam), город из которого он приехал (gorod), год рождения (god_r). В векторе otm[1] хранятся три отметки, полученные на ЦТ, поле sr_bal предназначено для хранения среднего балла аттестата.

Пример 16.2. Описание переменных типа структура.

tchk A, B;

date d1, d2;

kniga K;

vector <student> gruppa (30);

Здесь описаны переменные А и В типа tchk (две точки); переменные d1 и d2 типа date (две даты); переменная K типа kniga и переменная gruppa, являющаяся массивом, содержащим описание для 30 студентов.

Пример 16.3. Инициализация структуры:

A = {3.2, -4.1};

K = {"Н.Я.Виленкин", "Комбинаторика", 400, 2013};

Точка А имеет координаты (3.2; -4.1): книга K — «Комбинаторика», автор — Н. Я. Виленкин, в ней 400 страниц, издана в 2013 г.

Пример 16.4. Обращение к полям структуры.

B.x = 1; B.y = -1;

cin >> d1.d >> d1.m >> d1.g;

if (K.str > 100)…;

cout << gruppa[2].otm[1]

Пример 16.5. Описание структуры для хранения отрезка, концы которого являются точками.

struct otrezok

{

  tchk beg, en;

};

Использование:

otrezok AB;

AB.beg.x = 0;

AB.beg.y = 0;

AB.en.x = 2;

AB.en.y = -3;

Или так

tchk A = {0,0}, B = {2, -3};

otrezok AB = {A, B};

Пример 16.6. Подсказка системы.


[1] При описании вектора в качестве поля структуры нельзя инициализировать элементы данных сразу в скобках (vector <int> otm(3)), нужно присвоить полю инициализируемое значение.

16.2. Использование структур для описания геометрических объектов

Простейшим геометрическим объектом на плоскости является точка, которая задается своими координатами. Точка описана в примере 16.1. Пара точек на плоскости определяет отрезок, который описан в примере 16.5.

Еще одним важным геометрическим объектом на плоскости является прямая. В математике используют разные способы описать прямую с помощью уравнений. Уравнение прямой на плоскости в прямоугольной системе координат — это некоторое уравнение с двумя переменными x и y, которое обращается в тождество при подстановке в него координат любой точки этой прямой. Любая форма уравнения прямой имеет параметры. Используя параметры уравнения, можно описать соответствующую структуру (пример 16.7). Разные формы уравнения прямой (в большинстве случаев) могут быть приведены друг к другу, поскольку они описывают один и тот же объект. Использование той или иной формы уравнения прямой зависит от задачи. Уравнение прямой в общем виде является наиболее универсальным. Любая другая форма уравнения прямой всегда может быть приведена к общему уравнению прямой.

Пример 16.8. Известны координаты двух точек, через которые проходит прямая. Получить запись уравнения этой прямой в общем виде.

Этапы выполнения задания

I. Исходные данные: переменная p1 (структура, описывающая уравнение прямой, проходящей через две точки).

II. Результат: переменная p2 (структура, описывающая уравнение прямой в общем виде).

III. Алгоритм решения задачи.

1. Ввод исходных данных. Вводим координаты двух точек и создаем из них структуру p1.
2. Для того чтобы из одной структуры получить другую, создадим функцию tchk_to_pr.
3. Для получения соответствующих коэффициентов выполним следующие тождественные преобразования уравнения прямой, проходящей через две точки.

begin mathsize 18px style left parenthesis x space – space x subscript 1 right parenthesis left parenthesis y subscript 2 – space y subscript 1 right parenthesis space equals space left parenthesis y space – space y subscript 1 right parenthesis left parenthesis x subscript 2 space – space x subscript 1 right parenthesis space left right double arrow left right double arrow left parenthesis y subscript 2 – space y subscript 1 right parenthesis x space minus left parenthesis y subscript 2 space minus space y subscript 1 right parenthesis space x subscript 1 space minus space left parenthesis x subscript 2 minus space x subscript 1 right parenthesis space y space plus space left parenthesis x subscript 2 minus space x subscript 1 right parenthesis space y subscript 1 equals 0 end style

begin mathsize 18px style A space equals space y subscript 2 space minus space y subscript 1 semicolon space space space B space equals space x subscript 1 space minus space x subscript 2 semicolon space space C space equals space space y subscript 1 x subscript 2 space minus space x subscript 1 y subscript 2 end style

4. Вывод результата.

IV. Описание переменных: p1, p2 – struct.

Пример 16.9. Известны координаты точки и коэффициенты уравнения прямой в общем виде. Определить, принадлежит ли точка прямой.

Этапы выполнения задания

I. Исходные данные: переменная АВ (структура, описывающая уравнение прямой в общем виде), А (структура, описывающая точку).

II. Результат: сообщение «да» или «нет».

III. Алгоритм решения задачи.

1. Ввод исходных данных.
2. Для того чтобы проверить, лежит ли точка на прямой, создадим функцию tchk_na_pr.
3. Точка лежит на прямой, если при подстановке ее координат в уравнение прямой получим верное равенство (для общего уравнения должны получить 0). Поскольку вычисления проходят в вещественных числах, то будем проверять, что полученное значение по модулю меньше, чем 10-6. Такой точности на практике обычно бывает достаточно.
4. Вывод результата.

IV. Описание переменных: A, AB – struct.

Пример 16.10. Известны координаты концов отрезка и коэффициенты уравнения прямой в общем виде. Определить, имеют ли прямая и отрезок общие точки.

Этапы выполнения задания

I. Исходные данные: переменная CD (структура, описывающая уравнение прямой в общем виде), АB (структура, описывающая отрезок).

II. Результат: сообщение «да» или «нет».

III. Алгоритм решения задачи.

1. Ввод исходных данных. Структуру AB создаем по введенным координатам двух точек.

2. Для того чтобы проверить, имеют ли прямая и отрезок общие точки, создадим функцию otr_na_pr.

3. Отрезок имеет с прямой общие точки, если выполняется одно из условий:

3.1. Один из концов отрезка лежит на прямой.
3.2. Оба конца отрезка лежат на прямой.
3.3. Прямая пересекает отрезок.

4. Если точка лежит на прямой, то при подстановке ее координат в уравнение, в левой части общего уравнения прямой получаем 0. Если точка не принадлежит прямой, то получаем одно из двух неравенств: begin mathsize 16px style A x space plus space B y space plus space C space less than space 0 end style  или   A x space plus space B y space plus space C space greater than space 0. Каждое из неравенств определяет полуплоскость относительно заданной прямой. Прямая пересекает отрезок, если его концы находятся в разных полуплоскостях относительно заданной прямой.

5. Поскольку вычисления проходят в вещественных числах, то будем проверять, что полученное значение по модулю меньше, чем 10-6. Такой точности на практике обычно бывает достаточно.

6. Вывод результата.

IV. Описание переменных: CD, AB – struct.

Пример 16.11. Многоугольник задан списком своих вершин в порядке обхода. Для каждой вершины известны ее координаты на плоскости. Найти периметр многоугольника.

Этапы выполнения задания

I. Исходные данные: n — количество точек, a — массив точек.

II. Результат: периметр многоугольника.

III. Алгоритм решения задачи.

1. Ввод исходных данных. Создаем массив из точек и вводим координаты.
2. Каждая сторона многоугольника — это отрезок, соединяющий вершины с соседними номерами. Для того, чтобы не обрабатывать отдельно сторону, соединяющую последнюю вершину с начальной, добавим координаты начальной вершины в конец вектора.
3. Для вычисления периметра создадим функцию, которая будет вычислять длину отрезка.
4. В цикле переберем пары соседних вершин и вычислим их длины. Сумма длин — искомый периметр.
5. Вывод результата.

IV. Описание переменных: n – int, a – vector<tchk>.

Пример 16.7. Формы записи уравнения прямой и соответствующие им описания структур.

Уравнение прямой с угловым коэффициентом: y = kx + l. Уравнение не позволяет описать прямую, параллельную оси OY.

struct pr_ugl_kf

{

  double k, l;

};

Уравнение прямой в отрезках: begin mathsize 16px style x over a space plus space y over b space equals space 1. end style Параметры а и b — величины отрезков, отсекаемых прямой на осях координат. Уравнение не позволяет описать прямую, проходящую через начало координат.

struct pr_v_otr

{

  double a, b;

};

Уравнение прямой, проходящей через две точки begin mathsize 16px style A left parenthesis x subscript 1 comma space space y subscript 1 right parenthesis end style) и  B left parenthesis x subscript 2 comma space space y subscript 2 right parenthesis:

begin mathsize 16px style left parenthesis x space minus space x subscript 1 right parenthesis left parenthesis y subscript 2 space minus space y subscript 1 right parenthesis space equals space left parenthesis y space minus space y subscript 1 right parenthesis left parenthesis x subscript 2 space minus space x subscript 1 right parenthesis end style

struct pr_2_tchk

{

  tchk A, B; 

};

Общее уравнение прямой:

struct pr

{

  double A, B, C;

};

Пример 16.8.

V. Программа:

#include <iostream>

 

using namespace std;

 

struct tchk

{

  double x, y;

};

 

struct pr_2_tchk

{

    tchk A, B;

};

 

struct pr

{

    double A, B, C;

};

 

pr tchk_to_pr(pr_2_tchk t)

{

  pr t1;

  t1.A = t.B.y - t.A.y;

  t1.B = t.A.x - t.B.x;

  t1.C = t.A.y * t.B.x - t.A.x * t.B.y;

  return t1;

}

 

int main()

{

  tchk A, B;

  cout << "x1, y1" << endl;

  cin >> A.x >> A.y;

  cout << "x2, y2" << endl;

  cin >> B.x >> B.y;

  pr_2_tchk p1 = {A, B};

  pr p2 = tchk_to_pr (p1);

  cout << "obschee uravnenie: ";

  cout << p2.A << "x + ";

  cout << p2.B << "y + " << p2.C;

  cout << " = 0" << endl;

  return 0;

}

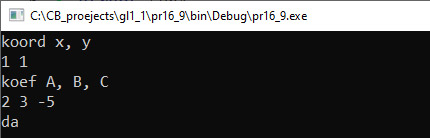
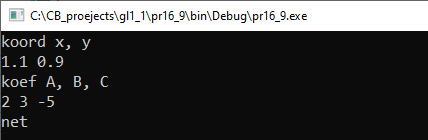
  VI. Тестирование.

Пример 16.9.

V. Программа:

#include <iostream>

#include <cmath>

 

using namespace std;

 

struct tchk

{

  double x, y;

};

 

struct pr

{

  double A, B, C;

};

 

bool tchk_na_pr(pr p, tchk t)

{

  double z = p.A * t.x + p.B * t.y + p.C;

  return (abs(z) <= 0.000001);

}

 

int main()

{

  tchk A;

  cout << "koord x, y" << endl;

  cin >> A.x >> A.y;

  pr AB;

  cout << "koef A, B, C" << endl;

  cin >> AB.A >> AB.B >> AB.C;

  if (tchk_na_pr(AB, A))

    cout << "da" << endl;

  else

    cout << "net" << endl;

  return 0;

}

 VI.  Тестирование.

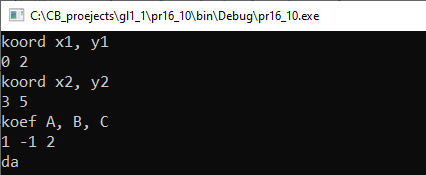
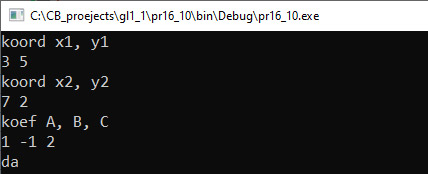
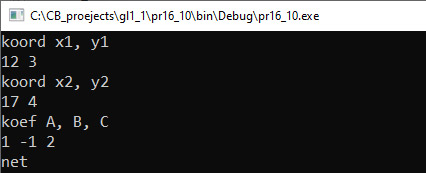
Пример 16.10.

V. Программа:

#include <iostream>

#include <cmath>

 

using namespace std;

 

struct tchk

{

  double x, y;

};

 

struct otrezok

{

  tchk beg, en;

};

 

struct pr

{

  double A, B, C;

};

 

bool otr_na_pr(pr p, otrezok t)

{

  double z1, z2;

  z1 = p.A * t.beg.x + p.B * t.beg.y + p.C;

  z2 = p.A * t.en.x + p.B * t.en.y + p.C;

  return (z1 * z2 < 0 ||

        abs(z1 * z2) <= 0.000001);

}

 

int main()

{

  tchk A, B;

  cout << "koord x1, y1" << endl;

  cin >> A.x >> A.y;

  cout << "koord x2, y2" << endl;

  cin >> B.x >> B.y;

  otrezok AB = {A, B};

  pr CD;

  cout << "koef A, B, C" << endl;

  cin >> CD.A >> CD.B >> CD.C;

  if (otr_na_pr(CD, AB))

    cout << "da" << endl;

  else

    cout << "net" << endl;

  return 0;

}

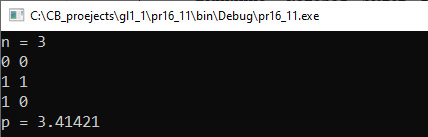
  VI. Тестирование.

Отрезок целиком лежит на прямой.

Один конец отрезка лежит на прямой.

Прямая пересекает отрезок.

Нет общих точек.

Пример 16.11.

V. Программа:

#include <iostream>

#include <vector>

#include <cmath>

 

using namespace std;

 

struct tchk

{

  double x, y;

};

 

double dlina (tchk A, tchk B)

{

  double dl;

  dl = sqrt((A.x - B.x) * (A.x - B.x) +

            (A.y - B.y) * (A.y - B.y));

  return dl;

}

 

int main()

{

  int n;

  cout << "n = ";

  cin >> n;

  vector <tchk> a(n);

  for (int i = 0; i < n; i++)

    cin >> a[i].x >> a[i].y;

  a.push_back(a[0]);

  double p = 0;

  for (int i = 0; i < n; i++)

    p += dlina(a[i], a[i + 1]);

  cout << "p = " << p << endl;

  return 0;

}

 VI. Тестирование.

16.3. Использование структур для описания даты и времени

Пример 16.12. Текущее время задано в часах, минутах и секундах. Который час будет через k секунд?

Этапы выполнения задания

I. Исходные данные: v — структура, описывающая время, k — число секунд.

II. Результат: новое время.

III. Алгоритм решения задачи.

1. Ввод исходных данных.
2. Создадим две функции: tm_to_sek и sek_to_tm для перевода времени в секунды и секунд в формат времени (часы, минуты, секунды).

2.1. Переведем текущее время в секунды. Для этого просуммируем количество часов, умноженное на 3600 (количество секунд в часе), количество минут, умноженное на 60, и количество секунд. 
2.2. Увеличим секунды. 
2.3. Переведем секунды в формат времени. Секунды — это остаток от деления на 60 общего количества секунд. Минуты — это остаток от деления количества минут на 60.

3. Вывод результата.

IV. Описание переменных: k – int, v – struct.

Пример 16.13. Заданы две даты. Определить количество дней между ними.

Этапы выполнения задания

I. Исходные данные: d1, d2 — структуры, описывающие даты.

II. Результат: число дней между двумя датами.

III. Алгоритм решения задачи.

1. Ввод исходных данных.
2. Во многих программах (например, в Excel) дата хранится в виде числа. Это число — количество дней, прошедших от какой-то начальной даты. Часто за начало отсчета берется дата 01.01.1900. Переведем каждую дату в целое число. Расчет будем вести от 01.01.1900. Тогда порядковый номер дня (d.m.g) можно посчитать по формуле:

begin mathsize 18px style straight N space equals space straight d space plus space straight d subscript 1 space plus space straight d subscript 2 space plus space... space plus space straight d subscript straight m space minus space 1 end subscript space plus space left parenthesis straight g space minus space 1900 right parenthesis space asterisk times space 365 space plus space left parenthesis straight g space – space 1900 right parenthesis divided by 4 comma end style

где d  — номер дня в дате, d1, d2, ... dm - 1 — количество дней в месяцах, предшествующих заданному, (y – 1900) * 365 — количество дней за полный прошедший год до текущей даты, (g – 1900)/4  — количество дней, которые нужно добавить за прошедшие високосные годы. Формула буде верной для дат от 01.01.1900 до 28.02.2100. (2100 год не является високосным, поскольку 2100 делится на 100, но не делится на 400).

3. Создадим функцию date_to_int.
4. Вычислим порядковые номера для каждой даты.
5. Найдем разность между двумя порядковыми номерами.
6. Вывод результата.

IV. Описание переменных: d1, d2 – struct.

Пример 16.12.

V. Программа:

#include <iostream>

 

using namespace std;

 

struct vremja

{

  int ch, m, s;

};

 

int vr_to_sek(vremja t)

{

  int N;

  N = t.ch * 3600 +t.m *60 + t.s;

  return N;

}

 

vremja sek_to_vr (int N)

{

  vremja t;

  t.s = N % 60;

  t.m = N / 60 %60;

  t.ch = N / 3600 % 24;

  return t;

}

 

int main()

{

  vremja v;

  cout << "vremja" << endl;

  cin >> v.ch >> v.m >> v.s;

  int k;

  cout << "k = ";

  cin >> k;

  int sek = vr_to_sek(v);

  sek += k;

  vremja v1 = sek_to_vr(sek);

  cout << v1.ch << ":";

  cout << v1.m << ":";

  cout << v1.s << endl;

  return 0;

}

 VI. Тестирование.

Пример 16.13.

V. Программа:

#include <iostream>

#include <vector>

 

using namespace std;

 

struct date

{

  int d, m ,g;

};

int date_to_int(date t)

{

  vector <int> d = {31, 28, 31, 30, 
     31, 30, 31, 31, 30, 31, 30, 31};

  int N = t.d ;

  for (int i = 0; i < t.m - 1; i++)

    N += d[i];

  N += (t.g - 1900) * 365; 

  N += (t.g - 1900) / 4;

  if (t.g != 1900 && t.g % 4 == 0 &&

   (t.m == 1 || t.m ==2 && t.d < 29))

    N--;

  return N;

}

 

int main()

{

  date d1, d2;

  cout << "1 data" << endl;

  cin >> d1.d >> d1.m >> d1.g;

  cout << "2 data" << endl;

  cin >> d2.d >> d2.m >> d2.g;

  int n_d1 = date_to_int(d1);

  int n_d2 = date_to_int(d2);

  int k = abs(n_d1 - n_d2);

  cout << " mezdu datami " ;

  cout << k <<  " dnei" << endl;

  return 0;

}

 VI. Тестирование.

В функции преобразования необходима дополнительная проверка для случая, если текущий год является високосным. Тогда дополнительный номер должен быть добавлен только к датам после 28 февраля. 1900 г. исключается, поскольку он не является високосным. 

Вопросы к параграфу

1. Какой тип данных называют структурой?

2. Как называется отдельный элемент структуры?

3. Как описываются структуры?

4. Какие структуры можно использовать для описания геометрических объектов?

5. Какие структуры можно использовать для описания даты и времени?

Упражнения

    

1. Напишите программу, которая преобразует уравнение прямой в отрезках в общее уравнение прямой.

2. Напишите программу, которая преобразует общее уравнение прямой в уравнение прямой с угловым коэффициентом. Предусмотреть проверку случая, когда это сделать невозможно.

3. Напишите программу, которая преобразует уравнение прямой, проходящей через две точки, в уравнение прямой с угловым коэффициентом. Если это невозможно, то получить уравнение в виде .

4. Напишите программу, которая определит взаимное расположение точки с координатами (x0, y0) и прямой .

5. Напишите программу, которая определит взаимное расположение точек с координатами (x1, y1), (x2, y2) и прямой .

6. Напишите программу, которая определит взаимное расположение точки с координатами (x0, y0) и двух параллельных прямых  и .

7. Многоугольник задан списком своих вершин в порядке обхода. Для каждой вершины известны ее координаты на плоскости. Найдите длину самой короткой диагонали многоугольника.

8. Многоугольник задан списком своих вершин в порядке обхода. Для каждой вершины известны ее координаты на плоскости. Получите массив прямых, заданных уравнением прямой, проходящей через две точки. Каждая прямая проходит через сторону многоугольника. Преобразуйте каждое уравнение в общее уравнение прямой. Выведите эти уравнения. * Есть ли у многоугольника две разные стороны, лежащие на одной прямой (это может быть у невыпуклого многоугольника)?

9. Для проверки того, что точка (x0, y0) лежит внутри треугольника, заданного вершинами (x1, y1), (x2, y2), (x3, y3), можно воспользоваться следующим алгоритмом:

    1. Провести прямую через точки (x1, y1), (x2, y2).
    2.  Если точки (x0, y0) и (x3, y3) лежат в разных полуплоскостях относительно этой прямой, то точка (x0, y0) лежит снаружи.
    3. Если точки (x0, y0) и (x3, y3) лежат в одной полуплоскости, то произвести аналогичные проверки для остальных вершин.
    4. Если для всех трех прямых точка (x0, y0) и оставшаяся вершина лежат в одной полуплоскости, то точка (x0, y0) внутри треугольника.

Реализовать описанный выше алгоритм.

10*. Написать программу для проверки, лежит ли точка (x0, y0) внутри выпуклого многоугольника.

11. Вводятся два значения времени: часы, минуты, секунды. Сколько секунд прошло между ними? Время указано в пределах одних суток.

12. Вводятся два значения времени: часы, минуты, секунды. Между ними могло пройти более суток (но не более двух суток). Сколько прошло времени между ними? Ответ получить в часах, минутах и секундах.

13. Вводится дата: день, месяц, год. Уменьшить введенную дату на t дней.

14. Дана дата. Вывести, сколько дней до нее осталось (или сколько дней прошло).

15. Вводится дата: месяц, год. Определить день недели. Для определения дня недели можно воспользоваться следующими формулами:

a = (14 − месяц) / 12
y = год − a
m = месяц + 12 * a − 2
ДеньНедели = (день + y + y / 4 − y / 100 + y / 400 + (31 * m) / 12) % 7
Все деления целочисленные. Результат: 0 — воскресенье, 1 — понедельник и т. д

16. Дана дата. Сгенерировать расписание с этой даты на t дней по такому принципу: сутки через трое. Если рабочий день приходится на воскресенье, то он переносится на понедельник. В итоге показать даты рабочих дней.

17*.  Дан режим работы интернет-магазина. ПН 9:00 — 21:00, ВТ 9:00 — 21:00, СР 9:00 — 21:00, ЧТ 9:00 — 21:00, ПТ 9:00 — 21:00, СБ 10:00 — 18:00, ВС 10:00 — 18:00. И даны дата и время. Определить, работает ли в это время магазин и сколько минут до конца рабочей смены.