§ 15. Двумерные массивы

15.3. Обработка двумерных массивов

Обработка двумерных массивов позволяет получить какие-то результаты путем анализа данных в массиве. Сам массив при этом не изменяется. Задачи поиска элементов, удовлетворяющих условию, подсчета суммы, поиска максимального и др. во многом решаются аналогично тому, как это происходило для линейных массивов.

Пример 15.8. Задан двумерный массив d из m строк и n столбцов. Посчитать сумму тех элементов массива, у которых сумма квадратов номера строки и номера столбца равна заданному числу x.

Этапы выполнения задания

I.  Исходные данные: переменные m и n (количество строк и столбцов в массиве), d — двумерный массив, x (число).

II.  Результат: переменная s (сумма искомых элементов).

III. Алгоритм решения задачи.

1. Ввод исходных данных. Массив вводится поэлементно. 
2. Определение начального значения для суммы (s = 0). 
3. Проверяем текущий элемент. Если он удовлетворяет условию, то добавляем его к сумме. 
4. Вывод результата.

IV. Описание переменных: n, x, s – int, d – vector<vector <int>>

Пример 15.9. Задан двумерный массив d из m сток и n столбцов. Определить, есть ли в массиве хотя бы один элемент, кратный x. Если да, то вывести индексы его местоположения.

Этапы выполнения задания

I. Исходные данные: переменные m и n (количество строк и столбцов в массиве), d — двумерный массив, x (число).

II. Результат: переменные r, c (номера строки и столбца, в которых найден элемент) или сообщение «не найден».

III. Алгоритм решения задачи.

1. Ввод исходных данных. Массив заполняется случайными числами. 
2. Определение начального значения для искомых индексов (r = -1, c = -1). 
3. Проверка текущего элемента. Если он удовлетворяет условию, то меняем значения r и c. 
4. Вывод результата. Если переменные r и c не изменились, то выводим сообщение, что элемент не найден, иначе выводим их значения.

IV. Описание переменных: n, x, r, c – int, d – vector<vector <int>>

Если в массиве несколько элементов, удовлетворяющих условию задачи, то будет выведен последний найденный элемент. Если нужен первый элемент, то можно ввести дополнительную переменную-флаг, которая будет равна true, пока значения r и c не изменились. После их изменения она станет false и значения r и c больше меняться не будут (пример 15.10).

Пример 15.11. Задан двумерный массив d из m строк и n столбцов. Найти минимальный и максимальный элементы и вывести индексы их местоположения.

Этапы выполнения задания

I. Исходные данные: переменные m и n — количество строк и столбцов в массиве, d — двумерный массив, x — число.

II. Результат: переменные r_min, c_min, r_max, c_max — номера строки и столбца, в которых найден элемент.

III. Алгоритм решения задачи.

1. Ввод исходных данных. Массив заполняется случайными числами.
2. Определение начального значения для искомых индексов (r_min = 0, c_min = 0, r_max = 0, c_max = 0).
3. Проверяем текущий элемент. Если он больше текущего максимального, то меняем значения r_max, c_max.
4. Проверяем текущий элемент. Если он меньше текущего минимального, то меняем значения r_min, c_min.
5. Вывод результата.

IV. Описание переменных: n, m, n_min, c_min, r_max, c_max – int, d – vector<vector <int>>

Если в массиве несколько элементов, равных максимальному (минимальному), то будет выводиться местоположение первого из таких элементов. Если нужно получить местоположение последнего, то достаточно заменить знак «>» («<») на «>=» («<=»).

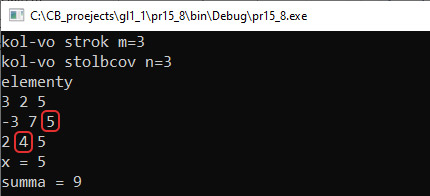
Пример 15.8.

V. Программа:

#include <iostream>

#include <vector>

 

using namespace std;

 

int main()

{

  int m, n;

  cout << "kol-vo strok m=";

  cin >> m;

  cout << "kol-vo stolbcov n=";

  cin >> n;

  cout << "elementy" << endl;

  vector <vector <int>> d(m, vector <int> (n));

  for (int i = 0; i < m; i++)

    for (int j = 0; j < n; j++)

      cin >> d[i][j];

  int x;

  cout << "x = ";

  cin >> x;

  int s = 0;

  for (int i = 0; i < m; i++)

    for (int j = 0; j < n; j++)

      if (i * i + j * j == x)

        s += d[i][j];

  cout << "summa = " << s << endl;

  return 0;

}

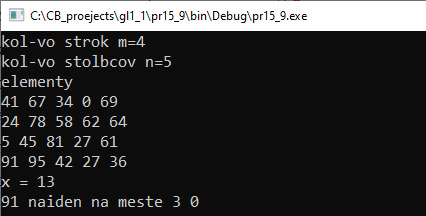
 VI. Тестирование.

VII. Анализ результатов. Будут просуммированы элементы, имеющие номера [1][2] и [2][1] (они выделены).

В математике для матрицы определены понятия главная диагональ и побочная диагональ. На главной диагонали находятся элементы матрицы d[i][j], для которых верно условие i = j. Для элементов побочной диагонали: i + j = n – 1 (n — число столбцов, нумерация с 0).

Пример 15.9.

V. Программа:

#include <iostream>

#include <vector>

#include <ctime>

#include <cstdio>

 

using namespace std;

 

int main()

{

  srand(time(NULL));

  int m, n;

  cout << "kol-vo strok m=";

  cin >> m;

  cout << "kol-vo stolbcov n=";

  cin >> n;

  cout << "elementy" << endl;

  vector <vector <int>> d(m, vector <int> (n));

  for (int i = 0; i < m; i++){

    for (int j = 0; j < n; j++){

      d[i][j] = rand() % 100;

      cout << d[i][j] << " ";

    }

    cout << endl;

  }

  int x;

  cout << "x = ";

  cin >> x;

  int r = -1, c = -1;

  for (int i = 0; i < m; i++)

    for (int j = 0; j < n; j++)

      if (d[i][j] % x == 0){

        r = i;

        c = j;

      }

  if (r == -1 && c == -1)

    cout << "ne naiden";

  else {

    cout << d[r][c];

    cout << " naiden na meste ";

    cout << r << " " << c;

  }

  cout << endl;

  return 0;

}

 VI. Тестирование.

Пример 15.10. Фрагмент программы:

bool f = true;

for (int i = 0; i < m; i++)

  for (int j = 0; j < n; j++)

    if (f && d[i][j] % x == 0){

      r = i;

      c = j;

       f = false;

    }

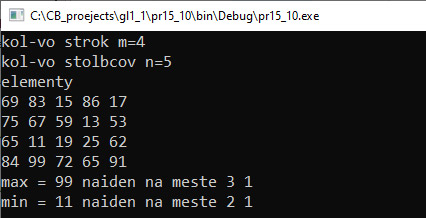
Пример 15.11.

V. Программа:

#include <iostream>

#include <vector>

#include <ctime>

#include <cstdio>

 

using namespace std;

 

int main()

{

  srand(time(NULL));

  int m, n;

  cout << "kol-vo strok m=";

  cin >> m;

  cout << "kol-vo stolbcov n=";

  cin >> n;

  cout << "elementy" << endl;

  vector <vector <int>> d(m, vector <int> (n));

  for (int i = 0; i < m; i++){

    for (int j = 0; j < n; j++){

      d[i][j] = rand() % 100;

      cout << d[i][j] << " ";

    }

    cout << endl;

  }

  int r_min = 0, c_min = 0;

  int r_max = 0, c_max = 0;

  for (int i = 0; i < m; i++){

    for (int j = 0; j < n; j++){

      if (d[i][j] > d[r_max][c_max]){

       r_max = i;

       c_max = j;

     }

     if (d[i][j] < d[r_min][c_min]){

       r_min = i;

       c_min = j;

    }

  }

  cout << "max = " << d[r_max][c_max];

  cout << " naiden na meste ";

  cout << r_max << " " << c_max;

  cout << endl;

  cout << "min = " << d[r_min][c_min];

  cout << " naiden na meste ";

  cout << r_min << " " << c_min;

  cout << endl;

  return 0;

}

 VI. Тестирование.