Печатать книгуПечатать книгу

§ 15. Двумерные массивы

Сайт: Профильное обучение
Курс: Информатика. 10 класс (Повышенный уровень)
Книга: § 15. Двумерные массивы
Напечатано:: Гость
Дата: Пятница, 3 Май 2024, 01:44

Оглавление

15.1. Описание двумерного массива

Количество индексов, по которым обращаются к элементу в массиве, определяет размерность массива.

Кроме одномерных, могут использоваться двумерные, трехмерные и другие массивы.

Двумерный массив — массив, элементами которого являются одномерные массивы. Его можно представить как таблицу с данными, в которой каждая строка — линейный массив. Обращение к элементу осуществляется по двум индексам: a[3][5] — элемент, находящийся в строке, имеющей индекс три, и столбце с индексом пять. Примером использования двумерного массива является лист электронной таблицы.

Двумерный массив описывают следующим образом:

vector <vector <тип элементов>> имя_массива
(количество строк, vector <тип элементов>(количество столбцов));

Структура описания кажется достаточно сложной, однако она полностью отражает суть: двумерный вектор — линейный вектор, элементами которого являются линейные векторы. Второй параметр в круглых скобках указывает, каким значением нужно заполнить каждую строку. В примере 15.1 показано, как можно описывать двумерные векторы.

По аналогичной схеме можно описывать массивы больших размерностей.

Многомерные массивы используются в вычислительной математике. При  моделировании объектов, процессов и явлений многомерные массивы позволяют сохранять параметры модели и диапазоны их изменения.

Для многомерных массивов используют следующие названия: одномерный массив — вектор, двумерный массив — матрица (прямоугольная таблица), трехмерный массив — куб (набор однотипных таблиц).

Для определения многомерного массива большей размерности используют понятие тензор. Четырехмерный, пятимерный, многомерный массив — тензор.

Пример 15.1. Описание двумерных массивов.

Описание двумерного массива целых чисел из 10 строк и 10 столбцов.

  vector <vector <int>> d(10, vector <int> (10));  

Описание двумерного массива, размеры которого вводят с клавиатуры:

cout << "kol-vo strok i";

cout << "stolbcov" << endl;

cin >> m >> n;

vector <vector <int>> d(m, vector <int> (n));

Использование typedef (определение типа) для описания двумерного массива:

typedef vector <int> lv;

int main()

{

  int n, m;

  cout << "kol-vo strok i";

  cout << "stolbcov" << endl;

  cin >> m >> n;

  vector <lv> d(n, lv (m));

…

15.2. Формирование двумерных массивов

Значения элементов двумерного массива можно задавать теми же способами, что и элементов одномерного массива.

Константные значения элементам массива можно задать при описании, заключив их в фигурные скобки (пример 15.2). Количество строк и столбцов при этом не указывают, размеры определяются автоматически.

Данные в массив могут быть прочитаны с клавиатуры (пример 15.3) или из файла. Задавать значения элементам можно случайным образом (пример 15.4). Для того, чтобы обратится к каждому элементу двумерного массива, необходимо два вложенных цикла: первый будет поочередно фиксировать номер строки, а второй перебирать все элементы данной строки.

Выводят элементы двумерного массива в виде таблицы, переводя курсор после вывода очередной строки (вывод элементов реализован при получении случайных значений в (примере 15.4).

Если в массиве есть числа с разным количеством цифр, то в качестве разделителя между элементами в одной строке можно использовать символ табуляции (пример 15.5) или задать ширину для вывода значения с помощью команды (пример 15.6)

Пример 15.7.Задано число n. Сформировать двумерный массив из n строк и n столбцов, который выглядит следующим образом:

Этапы выполнения задания

I. Исходные данные: число n.

II. Результат: двумерный массив d.

III. Алгоритм решения задачи.

1. Ввод исходных данных.
2. Заполнять массив будем в цикле следующим образом:

2.1. При описании все элементы равны 0.
2.2. Элементы в первой и последней строках, а также в первом и последнем столбцах равны 1.
2.3. Элементы на диагонали равны номеру строки +1.

3. Вывод результата.

IV. Описание переменных:
n – int, d – vector<vector <int>>.

Пример 15.2. Константные значения в двумерном массиве:

vector <vector <int>> d = 

               {{1, 0, 0},

                {0, 1, 0},

                {0, 0, 1}};

Пример 15.3. Ввод элементов с клавиатуры:

cin >> m >> n; 

vector< vector<int> > d(m, vector <int>(n));

for (int i = 0; i < m; i++)

  for (int j = 0; j < n; j++)

    cin >> d[i][j];

Пример 15.4. Случайные значения [-5, 5]:

cin >> m >> n;

vector< vector<int> > d(m, vector <int>(n));

for (int i = 0; i < m; i++) {

  for (int j = 0; j < n; j++){

    d[i][j] = rand() % 11 - 5;

    cout << d[i][j] << " ";

  }

  cout << endl;

}

Пример 15.5. Вывод элементов через табуляцию:

for (int i = 0; i < m; i++) {

  for (int j = 0; j < n; j++)

    cout << d[i][j] << '\t';

  cout << endl;

}

Пример 15.6. Вывод элементов с установкой ширины печати:

for (int i = 0; i < m; i++) {

  for (int j = 0; j < n; j++)

    cout << setw(5) << d[i][j];

  cout << endl;

}

Результат вывода из примеров 15.5 и 15.6.

Пример 15.7.

V. Программа:

#include <iostream>

#include <vector>

#include <iomanip>

 

using namespace std;

 

int main()

{

  int n;

  cout << "n = ";

  cin >> n;

  vector <vector <int>> d(n, vector <int> (n));

  for (int i = 0; i < n; i++){

    d[0][i] = 1;

    d[n - 1][i] = 1;

    d[i][0] = 1;

    d[i][n - 1] = 1;

    d[i][i] = i + 1;

  }

  for (int i = 0; i < n; i++){

    for (int j = 0; j < n; j++)

      cout << setw(3) << d[i][j];

    cout << endl;

  }

  return 0;

}

VI. Тестирование.

15.3. Обработка двумерных массивов

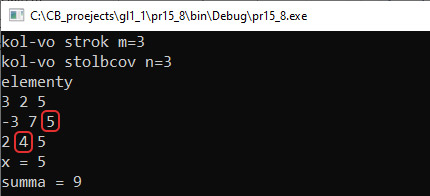
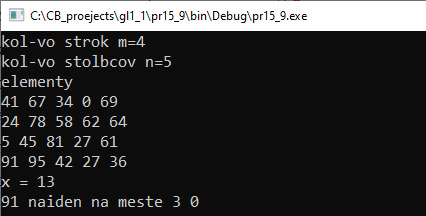
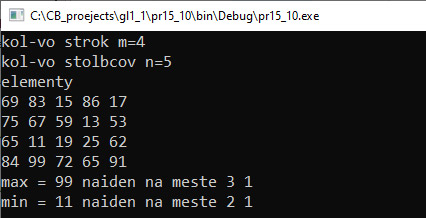
Обработка двумерных массивов позволяет получить какие-то результаты путем анализа данных в массиве. Сам массив при этом не изменяется. Задачи поиска элементов, удовлетворяющих условию, подсчета суммы, поиска максимального и др. во многом решаются аналогично тому, как это происходило для линейных массивов.

Пример 15.8. Задан двумерный массив d из m строк и n столбцов. Посчитать сумму тех элементов массива, у которых сумма квадратов номера строки и номера столбца равна заданному числу x.

Этапы выполнения задания

I.  Исходные данные: переменные m и n (количество строк и столбцов в массиве), d — двумерный массив, x (число).

II.  Результат: переменная s (сумма искомых элементов).

III. Алгоритм решения задачи.

1. Ввод исходных данных. Массив вводится поэлементно. 
2. Определение начального значения для суммы (s = 0). 
3. Проверяем текущий элемент. Если он удовлетворяет условию, то добавляем его к сумме. 
4. Вывод результата.

IV. Описание переменных: n, x, s – int, d – vector<vector <int>>

Пример 15.9. Задан двумерный массив d из m сток и n столбцов. Определить, есть ли в массиве хотя бы один элемент, кратный x. Если да, то вывести индексы его местоположения.

Этапы выполнения задания

I. Исходные данные: переменные m и n (количество строк и столбцов в массиве), d — двумерный массив, x (число).

II. Результат: переменные r, c (номера строки и столбца, в которых найден элемент) или сообщение «не найден».

III. Алгоритм решения задачи.

1. Ввод исходных данных. Массив заполняется случайными числами. 
2. Определение начального значения для искомых индексов (r = -1, c = -1). 
3. Проверка текущего элемента. Если он удовлетворяет условию, то меняем значения r и c. 
4. Вывод результата. Если переменные r и c не изменились, то выводим сообщение, что элемент не найден, иначе выводим их значения.

IV. Описание переменных: n, x, r, c – int, d – vector<vector <int>>

Если в массиве несколько элементов, удовлетворяющих условию задачи, то будет выведен последний найденный элемент. Если нужен первый элемент, то можно ввести дополнительную переменную-флаг, которая будет равна true, пока значения r и c не изменились. После их изменения она станет false и значения r и c больше меняться не будут (пример 15.10).

Пример 15.11. Задан двумерный массив d из m строк и n столбцов. Найти минимальный и максимальный элементы и вывести индексы их местоположения.

Этапы выполнения задания

I. Исходные данные: переменные m и n — количество строк и столбцов в массиве, d — двумерный массив, x — число.

II. Результат: переменные r_min, c_min, r_max, c_max — номера строки и столбца, в которых найден элемент.

III. Алгоритм решения задачи.

1. Ввод исходных данных. Массив заполняется случайными числами.
2. Определение начального значения для искомых индексов (r_min = 0, c_min = 0, r_max = 0, c_max = 0).
3. Проверяем текущий элемент. Если он больше текущего максимального, то меняем значения r_max, c_max.
4. Проверяем текущий элемент. Если он меньше текущего минимального, то меняем значения r_min, c_min.
5. Вывод результата.

IV. Описание переменных: n, m, n_min, c_min, r_max, c_max – int, d – vector<vector <int>>

Если в массиве несколько элементов, равных максимальному (минимальному), то будет выводиться местоположение первого из таких элементов. Если нужно получить местоположение последнего, то достаточно заменить знак «>» («<») на «>=» («<=»).

Пример 15.8.

V. Программа:

#include <iostream>

#include <vector>

 

using namespace std;

 

int main()

{

  int m, n;

  cout << "kol-vo strok m=";

  cin >> m;

  cout << "kol-vo stolbcov n=";

  cin >> n;

  cout << "elementy" << endl;

  vector <vector <int>> d(m, vector <int> (n));

  for (int i = 0; i < m; i++)

    for (int j = 0; j < n; j++)

      cin >> d[i][j];

  int x;

  cout << "x = ";

  cin >> x;

  int s = 0;

  for (int i = 0; i < m; i++)

    for (int j = 0; j < n; j++)

      if (i * i + j * j == x)

        s += d[i][j];

  cout << "summa = " << s << endl;

  return 0;

}

 VI. Тестирование.

VII. Анализ результатов. Будут просуммированы элементы, имеющие номера [1][2] и [2][1] (они выделены).

В математике для матрицы определены понятия главная диагональ и побочная диагональ. На главной диагонали находятся элементы матрицы d[i][j], для которых верно условие i = j. Для элементов побочной диагонали: i + j = n – 1 (n — число столбцов, нумерация с 0).

Пример 15.9.

V. Программа:

#include <iostream>

#include <vector>

#include <ctime>

#include <cstdio>

 

using namespace std;

 

int main()

{

  srand(time(NULL));

  int m, n;

  cout << "kol-vo strok m=";

  cin >> m;

  cout << "kol-vo stolbcov n=";

  cin >> n;

  cout << "elementy" << endl;

  vector <vector <int>> d(m, vector <int> (n));

  for (int i = 0; i < m; i++){

    for (int j = 0; j < n; j++){

      d[i][j] = rand() % 100;

      cout << d[i][j] << " ";

    }

    cout << endl;

  }

  int x;

  cout << "x = ";

  cin >> x;

  int r = -1, c = -1;

  for (int i = 0; i < m; i++)

    for (int j = 0; j < n; j++)

      if (d[i][j] % x == 0){

        r = i;

        c = j;

      }

  if (r == -1 && c == -1)

    cout << "ne naiden";

  else {

    cout << d[r][c];

    cout << " naiden na meste ";

    cout << r << " " << c;

  }

  cout << endl;

  return 0;

}

 VI. Тестирование.

Пример 15.10. Фрагмент программы:

bool f = true;

for (int i = 0; i < m; i++)

  for (int j = 0; j < n; j++)

    if (f && d[i][j] % x == 0){

      r = i;

      c = j;

       f = false;

    }

Пример 15.11.

V. Программа:

#include <iostream>

#include <vector>

#include <ctime>

#include <cstdio>

 

using namespace std;

 

int main()

{

  srand(time(NULL));

  int m, n;

  cout << "kol-vo strok m=";

  cin >> m;

  cout << "kol-vo stolbcov n=";

  cin >> n;

  cout << "elementy" << endl;

  vector <vector <int>> d(m, vector <int> (n));

  for (int i = 0; i < m; i++){

    for (int j = 0; j < n; j++){

      d[i][j] = rand() % 100;

      cout << d[i][j] << " ";

    }

    cout << endl;

  }

  int r_min = 0, c_min = 0;

  int r_max = 0, c_max = 0;

  for (int i = 0; i < m; i++){

    for (int j = 0; j < n; j++){

      if (d[i][j] > d[r_max][c_max]){

       r_max = i;

       c_max = j;

     }

     if (d[i][j] < d[r_min][c_min]){

       r_min = i;

       c_min = j;

    }

  }

  cout << "max = " << d[r_max][c_max];

  cout << " naiden na meste ";

  cout << r_max << " " << c_max;

  cout << endl;

  cout << "min = " << d[r_min][c_min];

  cout << " naiden na meste ";

  cout << r_min << " " << c_min;

  cout << endl;

  return 0;

}

 VI. Тестирование.

15.4. Преобразование двумерных массивов

Среди задач преобразования двумерного массива можно выделить следующие:

  • преобразование элементов массива в зависимости от условий;
  • обмен местами двух строк;
  • удаление строки;
  • вставка строки.

Решение этих задач во многом аналогично решению соответствующих задач для линейного массива.

Пример 15.12. Задан двумерный массив d из m строк и n столбцов. Поменять строки в матрице: первую с последней, вторую с предпоследней и т. д. Например:

Этапы выполнения задания

I. Исходные данные: переменные m и n — количество строк и столбцов в массиве, d — двумерный массив.

II. Результат: преобразованный массив.

III. Алгоритм решения задачи.

1. Ввод исходных данных (из файла). 
2. В цикле до половины от количества строк меняем местами два элемента линейного массива. 
3. Для обмена местами двух строк используем метод swap.
4. Вывод результата (в файл).

IV. Описание переменных: n, m – int, d – vector<vector <int>>

Пример 15.13. Задан двумерный массив d из m строк и n столбцов. Удалить  в нем столбцы с номерами от k1 до k2.

Этапы выполнения задания

 I. Исходные данные: переменные m и n — количество строк и столбцов в массиве), d — двумерный массив, k1 и k2 — номера столбцов.

II.  Результат: преобразованный массив.

III. Алгоритм решения задачи.

1. Ввод исходных данных (из файла).
2. Создаем массив b, который будет хранить в транспонированном виде наш исходный массив. В нем будем работать со строками. 
3. Используя метод erase, удалим диапазон данных, определяемый итераторами b.begin() + k1 и b.begin() + k2 + 1 (столбец k2 тоже нужно удалить, поэтому +1). 
4. Вывод результата (в файл). Для корректного вывода нужно поменять местами циклы, определяющие строку и столбец.

IV. Описание переменных: n, m, k1, k2 – int, d – vector<vector <int>>

При хранении двумерного вектора в памяти компьютера его строки записываются последовательно, друг за другом. Такое хранение не позволяет в явном виде выделить столбец матрицы. Если возникает необходимость обработки двумерного массива «по столбцам», то можно создать и использовать транспонированную [1]  матрицу.

Пример 15.12

V. Программа:

#include <iostream>

#include <fstream>

#include <vector>

 

using namespace std;

 

int main()

{

  ifstream fin("input.txt");

  ofstream fout ("output.txt");

  int m, n;

  fin >> m >> n;

  vector <vector <int>> d(m, vector <int> (n));

  for (int i = 0; i < m; i++)

    for (int j = 0; j < n; j++)

      fin >> d[i][j];

  for (int i = 0; i < m / 2; i++)

    d[i].swap(d[m - i - 1]);

  for (int i = 0; i < m; i++){

    for (int j = 0; j < n; j++)

      fout << d[i][j] << " ";

    fout << endl;

  }

  return 0;

}

 VI. Тестирование.

           

Пример 15.13.

 V. Программа:

#include <iostream>

#include <fstream>

#include <vector>

 

using namespace std;

 

int main()

{

  ifstream fin("input.txt");

  ofstream fout ("output.txt");

  int m, n;

  fin >> m >> n;

  vector <vector <int>> d(m, vector <int> (n));

  for (int i = 0; i < m; i++)

    for (int j = 0; j < n; j++)

      fin >> d[i][j];

  ///транспонирование

  vector <vector <int>> b(n, vector <int> (m));

  for (int i = 0; i < m; i++)

    for (int j = 0; j < n; j++)

      b[j][i] = d[i][j];

  int k1, k2;

  fin >> k1 >> k2;

  b.erase(b.begin() + k1, 
         b.begin() + k2 + 1);

  for (int j = 0; j < m; j++){

    for (int i = 0; i < b.size(); i++)

      fout << b[i][j] << " ";

    fout << endl;

  }

  return 0;

}

 VI. Тестирование.

  


[1] Транспонирование матрицы — операция над матрицей, когда ее столбцы становятся строками с теми же номерами.

Вопросы к параграфу

1. Что такое размерность массива?

2. Как описывается двумерный массив?

3. Как найти минимальный (максимальный) элемент в двумерном массиве?

4. Какие операции преобразования двумерного массива вы можете назвать?

Упражнения

    

1. Сформировать двумерные массивы из n строк и n столбцов, которые выглядит следующим образом:

1.  2. 
3.  4. 

2. Задан двумерный массив d из m сток и n столбцов. Найдите суммы тех элементов из массива, которые удовлетворяют следующим условиям.

    1. Разность номера строки и номера столбца равна 1.
    2. Модуль разности номера строки и номера столбца равен числу x.
    3. Кратны числу х.
    4. Расположены ниже главной диагонали.
    5. Расположены выше побочной диагонали.

3. Задан двумерный массив d из m сток и n столбцов. Определить, есть ли в массиве хотя бы один элемент, удовлетворяющий условию. Если да, то вывести индексы его местоположения.

    1. Равный пяти элемент.
    2. Элемент, являющийся отрицательным числом.
    3. Элемент, делящийся на 3 и на 5.
    4. Элемент, который при делении на 3 и на 5 дает нечетные остатки.

4. Задан двумерный массив d из m сток и n столбцов. Необходимо выполнить указанные действия.

    1. Вывести номер строки, содержащей минимальный элемент.
    2. Вывести номер столбца, содержащего максимальный элемент.
    3. Вывести номера всех строк, в которых есть элемент, равный минимальному.
    4. Вывести номера всех столбцов, в которых есть элемент, равный максимальному.

5. Задан двумерный массив d из m сток и n столбцов. Осуществить обмены.

    1. Столбцы 0 begin mathsize 18px style left right double arrow end style (m – 1), 1  begin mathsize 18px style left right double arrow end style (m – 2),  ... (первый с последним, второй с предпоследним...).
    2. Строки 0 begin mathsize 18px style rightwards double arrow end style 1, 1 begin mathsize 18px style rightwards double arrow end style 2, ..., (m – 1) begin mathsize 18px style rightwards double arrow end style 0 (циклически вниз на одну).
    3. Столбцы 1 begin mathsize 18px style rightwards double arrow end style 0, 2 begin mathsize 18px style rightwards double arrow end style 1, ... 0 begin mathsize 18px style rightwards double arrow end style (n – 1) (циклически влево на один).
    4. Строки 2 begin mathsize 18px style rightwards double arrow end style 0, 3 begin mathsize 18px style rightwards double arrow end style 1, 4 begin mathsize 18px style rightwards double arrow end style 2, ... (циклически вверх на две).

6. Задан двумерный массив d из m сток и n столбцов. Удалить указанные элементы.

    1. Строки, в которых есть числа, являющиеся полными квадратами.
    2. Строки, номера которых являются степенью двойки.
    3. Столбцы с номерами, кратными трем.
    4. Столбцы, в которых есть простые числа.