§ 26. Закон Ома для полной электрической цепи. КПД источника тока
В 1826 г. немецкий физик Георг Симон Ом (1787–1854) опытным путём установил, что при постоянной температуре отношение напряжения между концами металлического проводника к силе тока в нём является величиной постоянной. На основании этого был сформулирован закон, названный законом Ома для участка электрической цепи: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»I«/mi»«mo»=«/mo»«mfrac»«mi»U«/mi»«mi»R«/mi»«/mfrac»«/math», где R — сопротивление участка цепи. От чего и как зависит сила тока в замкнутой цепи, содержащей источник тока, т. е. в полной электрической цепи?
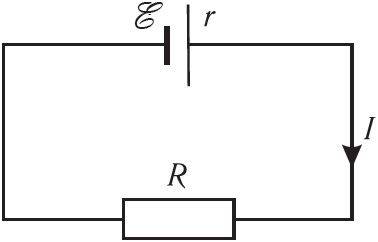
Закон Ома для полной электрической цепи. Рассмотрим электрическую цепь, состоящую из источника тока (гальванического элемента, аккумулятора или генератора) и резистора с сопротивлением R. Известны ЭДС «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨script¨»E«/mi»«/math» источника тока и его сопротивление r, которое называют внутренним. Схема цепи представлена на рисунке 132. Пусть сила тока в цепи I, а напряжение между концами проводника U.
Закон Ома для полной цепи связывает силу тока I в цепи, ЭДС «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨script¨»E«/mi»«/math» источника тока и полное сопротивление цепи R + r, которое складывается из сопротивлений внешнего (резистор) и внутреннего (источник тока) участков цепи (сопротивлением соединительных проводов пренебрегаем). Эту связь можно установить теоретически на основании закона сохранения энергии.
Если через поперечное сечение проводника за промежуток времени t проходит заряд q, то работу сторонней силы по перемещению электрического заряда можно определить по формуле
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»A«/mi»«mi»§#1089;§#1090;«/mi»«/msub»«mo»=«/mo»«mi mathvariant=¨script¨»E«/mi»«mi»q«/mi»«mo».«/mo»«/math»
Поскольку сила тока «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»I«/mi»«mo»=«/mo»«mfrac»«mi»q«/mi»«mi»t«/mi»«/mfrac»«/math», то
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»A«/mi»«mi»§#1089;§#1090;«/mi»«/msub»«mo»=«/mo»«mi mathvariant=¨script¨»E«/mi»«mi»I«/mi»«mi»t«/mi»«mo».«/mo»«/math»
(26.1)
В неподвижных проводниках неизменного химического состава в результате работы сторонних сил происходит увеличение только внутренней энергии внешнего и внутреннего участков цепи. Таким образом, при прохождении электрического тока в резисторе и источнике тока выделяется количество теплоты Q, которое можно определить по закону Джоуля–Ленца:
Q = I2Rt + I2rt.
(26.2)
На основании закона сохранения энергии:
Аст = Q.
(26.3)
Подставим формулы (26.1) и (26.2) в равенство (26.3) и в результате математических преобразований получим:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨script¨»E«/mi»«/math» = IR + Ir.
(26.4)
Произведение силы тока на сопротивление участка цепи часто называют падением напряжения на этом участке. Поэтому IR = U — падение напряжения (напряжение) на внешнем участке цепи, Ir — падение напряжения на внутреннем участке цепи.
Выражая силу тока из формулы (26.4), получим:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»I«/mi»«mo»=«/mo»«mfrac»«mi mathvariant=¨script¨»E«/mi»«mrow»«mi»R«/mi»«mo»+«/mo»«mi»r«/mi»«/mrow»«/mfrac»«mo».«/mo»«/math»
(26.5)
Формула (26.5) является математическим выражением закона Ома для полной электрической цепи, согласно которому сила тока в полной электрической цепи прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению цепи.
Аккумулятор, внутреннее сопротивление которого r = 0,80 Ом, подсоединён к резистору. Чему равна ЭДС аккумулятора, если напряжение на его полюсах U = 6,0 В, а сила тока в цепи I = 0,50 А?