§ 32-1. Вихревое электрическое поле. ЭДС индукции в движущихся проводниках
ЭДС индукции в движущихся проводниках. Рассмотрим металлический прямолинейный проводник длиной l, движущийся в неизменяющемся во времени магнитном поле так, что скорость «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover»«mi»v«/mi»«mo»§#8594;«/mo»«/mover»«/math» его движения перпендикулярна индукции магнитного поля «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover»«mi»B«/mi»«mo»§#8594;«/mo»«/mover»«/math» а также проводнику. Проводник тоже перпендикулярен «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover»«mi»B«/mi»«mo»§#8594;«/mo»«/mover»«/math» (рис. 184.3, а). Несмотря на отсутствие вихревого электрического поля, в проводнике возникает ЭДС индукции. Выясним причину её возникновения.
Очевидно, что свободные электроны в проводнике движутся вместе с ним. В магнитном поле на движущиеся заряженные частицы действует сила Лоренца. Под действием этой силы свободные электроны перемещаются к торцу «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»C«/mi»«mo»`«/mo»«/math» проводника (рис. 184.3, б). Это приводит к тому, что на одном конце проводника преимущественно накапливаются отрицательные заряды, а на другом — положительные, совместно создающие электрическое поле. Поэтому между концами проводника возникает разность потенциалов U.
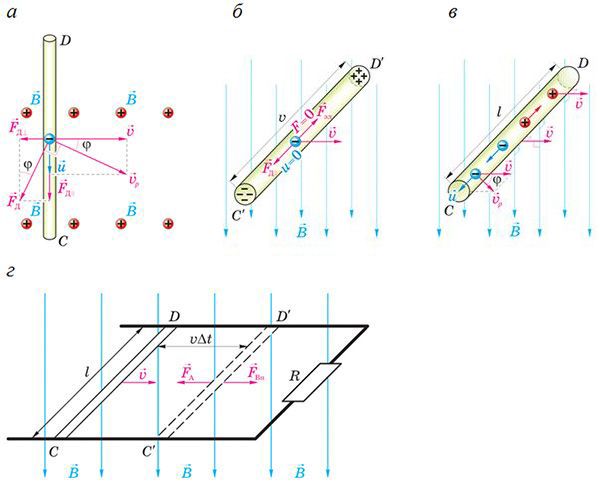
Пусть мгновенная скорость в начале упорядоченного движения электронов в системе отсчёта, связанной с проводником, равна «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover»«mi»u«/mi»«mo»§#8594;«/mo»«/mover»«/math» как только проводник пересекает границу магнитного поля. Тогда мгновенная скорость «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mover»«mi»v«/mi»«mo»§#8594;«/mo»«/mover»«mi mathvariant=¨normal¨»§#1088;«/mi»«/msub»«/math» движения электронов в инерциальной системе отсчёта, в которой задано стационарное магнитное поле, «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mover»«mi»v«/mi»«mo»§#8594;«/mo»«/mover»«mi mathvariant=¨normal¨»§#1088;«/mi»«/msub»«mo»=«/mo»«mover»«mi»u«/mi»«mo»§#8594;«/mo»«/mover»«mo»+«/mo»«mover»«mi»v«/mi»«mo»§#8594;«/mo»«/mover»«/math», причём направление скорости «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mover»«mi»v«/mi»«mo»§#8594;«/mo»«/mover»«mi mathvariant=¨normal¨»§#1088;«/mi»«/msub»«/math» составляет угол φ с направлением скорости «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover»«mi»v«/mi»«mo»§#8594;«/mo»«/mover»«/math» движения проводника (рис. 184.3, б). Если е — модуль заряда электрона, то модуль силы Лоренца, действующей на электрон со стороны магнитного поля, FЛ = еBυр, а её направление составляет угол 90° с направлением скорости «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mover»«mi»v«/mi»«mo»§#8594;«/mo»«/mover»«mi mathvariant=¨normal¨»§#1088;«/mi»«/msub»«/math» движения электрона.
На этом этапе движения свободных электронов сила Лоренца имеет две составляющие: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«mrow»«mi mathvariant=¨normal¨»§#1083;«/mi»«mo»§#8869;«/mo»«/mrow»«/msub»«/math», направленную перпендикулярно проводнику, и «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«mrow»«mi mathvariant=¨normal¨»§#1083;«/mi»«mo»§#8741;«/mo»«/mrow»«/msub»«/math», направленную вдоль проводника. Именно продольная составляющая силы Лоренца «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«mrow»«mi mathvariant=¨normal¨»§#1083;«/mi»«mo»§#8741;«/mo»«/mrow»«/msub»«/math» выполняет работу по разделению зарядов. Её модуль «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«mrow»«mi mathvariant=¨normal¨»§#1083;«/mi»«mo»§#8741;«/mo»«/mrow»«/msub»«mo»=«/mo»«msub»«mi»F«/mi»«mi mathvariant=¨normal¨»§#1083;«/mi»«/msub»«mi»cos§#966;«/mi»«mo»=«/mo»«mi»e«/mi»«mi»B«/mi»«msub»«mi»v«/mi»«mi mathvariant=¨normal¨»§#1088;«/mi»«/msub»«mi»cos§#966;«/mi»«mo»=«/mo»«mi»e«/mi»«mi»B«/mi»«mi»v«/mi»«/math». Перераспределение зарядов внутри проводника, связанное с увеличением абсолютного значения избыточных зарядов на его торцах, происходит до тех пор, пока сила, действующая на свободный электрон со стороны нарастающего электрического поля, не скомпенсирует продольную составляющую силы Лоренца: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»F«/mi»«mrow»«mi mathvariant=¨normal¨»§#1083;«/mi»«mo»§#8741;«/mo»«/mrow»«/msub»«mo»=«/mo»«msub»«mi»F«/mi»«mi»§#1101;§#1083;«/mi»«/msub»«/math», или «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»e«/mi»«mi»B«/mi»«mi»v«/mi»«mo»=«/mo»«mi»e«/mi»«mi»E«/mi»«/math» (1). Поскольку напряжённость однородного электрического поля внутри прямолинейного проводника связана с разностью потенциалов между его концами соотношением «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»E«/mi»«mo»=«/mo»«mfrac»«mi»U«/mi»«mi»l«/mi»«/mfrac»«/math» (2), то из уравнений (1) и (2) следует, что «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»U«/mi»«mo»=«/mo»«mi»B«/mi»«mi»v«/mi»«mi»l«/mi»«/math». Таким образом, сторонней силой, способствующей разделению зарядов в проводнике, является продольная составляющая силы Лоренца «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«mrow»«mi mathvariant=¨normal¨»§#1083;«/mi»«mo»§#8741;«/mo»«/mrow»«/msub»«/math».
Магнитное поле способствует разделению электрических зарядов в движущемся проводнике, однако не может служить источником энергии, так как магнитная сила, действующая на движущиеся электрические заряды, перпендикулярна скорости заряда, поэтому работа магнитных сил всегда равна нулю. В изолированном проводнике, движущемся с постоянной скоростью в стационарном магнитном поле, возникшая при разделении зарядов электрическая сила «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«mi»§#1101;§#1083;«/mi»«/msub»«/math» компенсирует действие продольной составляющей силы Лоренца «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«mrow»«mi mathvariant=¨normal¨»§#1083;«/mi»«mo»§#8741;«/mo»«/mrow»«/msub»«/math» и обращает в нуль скорость упорядоченного движения электронов «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover»«mi»u«/mi»«mo»§#8594;«/mo»«/mover»«mo»=«/mo»«mover»«mn»0«/mn»«mo»§#8594;«/mo»«/mover»«/math», следовательно, перпендикулярная составляющая силы Лоренца «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«mrow»«mi mathvariant=¨normal¨»§#1083;«/mi»«mo»§#8869;«/mo»«/mrow»«/msub»«/math» тоже оказывается равной нулю.
Превращение механической энергии в электрическую принято рассматривать при наличии индукционного тока. Рассмотрим прямоугольный контур, образованный металлическим проводником длиной l, находящимся на гладких проводящих горизонтальных шинах в вертикальном однородном магнитном поле, модуль индукции которого В (рис. 177.2, г). Правые концы шин подсоединены к резистору, электрическое сопротивление которого R. Сопротивление остальной части контура пренебрежимо мало. Если проводник скользит с постоянной скоростью «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover»«mi»v«/mi»«mo»§#8594;«/mo»«/mover»«/math», направленной горизонтально и перпендикулярно проводнику, то за промежуток времени Δt площадь поверхности, ограниченной контуром, изменится на величину «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo»§#8710;«/mo»«mi»S«/mi»«mo»=«/mo»«mo»-«/mo»«mi»l«/mi»«mi»v«/mi»«mo»§#8710;«/mo»«mi»t«/mi»«/math», а магнитный поток через эту поверхность — на «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo»§#8710;«/mo»«mi mathvariant=¨normal¨»§#1060;«/mi»«mo»=«/mo»«mo»-«/mo»«mi»B«/mi»«mi»l«/mi»«mi»v«/mi»«mo»§#8710;«/mo»«mi»t«/mi»«/math». Следовательно, в контуре наводится ЭДС индукции «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨script¨»E«/mi»«mi»§#1080;§#1085;§#1076;«/mi»«/msub»«mo»=«/mo»«mo»-«/mo»«mfrac»«mrow»«mo»§#8710;«/mo»«mi mathvariant=¨normal¨»§#1060;«/mi»«/mrow»«mrow»«mo»§#8710;«/mo»«mi»t«/mi»«/mrow»«/mfrac»«mo»=«/mo»«mi»B«/mi»«mi»l«/mi»«mi»v«/mi»«/math», обеспечивающая индукционный ток. Воспользовавшись законом Ома для полной цепи, выразим силу индукционного тока «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»I«/mi»«mi»§#1080;§#1085;§#1076;«/mi»«/msub»«mo»=«/mo»«mfrac»«msub»«mi mathvariant=¨script¨»E«/mi»«mi»§#1080;§#1085;§#1076;«/mi»«/msub»«mi»R«/mi»«/mfrac»«mo»=«/mo»«mfrac»«mrow»«mi»B«/mi»«mi»l«/mi»«mi»v«/mi»«/mrow»«mi»R«/mi»«/mfrac»«/math».
Однородное магнитное поле на прямолинейный участок проводника с током действует силой Ампера, модуль которой «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»F«/mi»«mi mathvariant=¨normal¨»§#1040;«/mi»«/msub»«mo»=«/mo»«msub»«mi»I«/mi»«mi»§#1080;§#1085;§#1076;«/mi»«/msub»«mi»l«/mi»«mi»B«/mi»«mo»=«/mo»«mfrac»«mrow»«msup»«mi»B«/mi»«mn»2«/mn»«/msup»«msup»«mi»l«/mi»«mn»2«/mn»«/msup»«mi»v«/mi»«/mrow»«mi»R«/mi»«/mfrac»«/math». Обеспечить движение проводника с постоянной скоростью можно, если скомпенсировать силу Ампера «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«mi mathvariant=¨normal¨»§#1040;«/mi»«/msub»«/math» внешней силой «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«mi»§#1074;§#1085;§#1077;§#1096;«/mi»«/msub»«mo»=«/mo»«mo»-«/mo»«msub»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«mi mathvariant=¨normal¨»§#1040;«/mi»«/msub»«/math». Воспользовавшись правилом левой руки, можно убедиться, что направление силы Ампера «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mover»«mi»F«/mi»«mo»§#8594;«/mo»«/mover»«mi mathvariant=¨normal¨»§#1040;«/mi»«/msub»«/math» противоположно направлению скорости «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover»«mi»v«/mi»«mo»§#8594;«/mo»«/mover»«/math» движения проводника (см. рис. 184.3, г), что согласуется с правилом Ленца. Мощность, развиваемая внешней силой, «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»P«/mi»«mi»§#1074;§#1085;§#1077;§#1096;«/mi»«/msub»«mo»=«/mo»«msub»«mi»F«/mi»«mi»§#1074;§#1085;§#1077;§#1096;«/mi»«/msub»«mi»v«/mi»«mo»=«/mo»«mfrac»«mrow»«msup»«mi»B«/mi»«mn»2«/mn»«/msup»«msup»«mi»l«/mi»«mn»2«/mn»«/msup»«msup»«mi»v«/mi»«mn»2«/mn»«/msup»«/mrow»«mi»R«/mi»«/mfrac»«mo»=«/mo»«msubsup»«mi»I«/mi»«mi»§#1080;§#1085;§#1076;«/mi»«mn»2«/mn»«/msubsup»«mi»R«/mi»«/math» совпадает с мощностью индукционного тока.
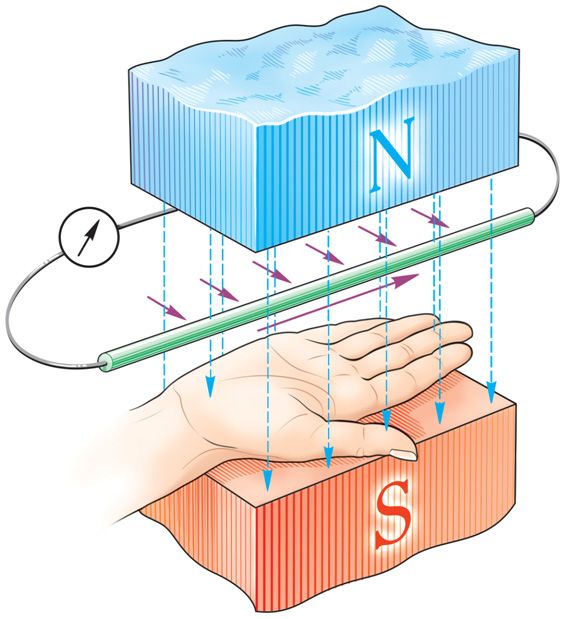
Направление индукционного тока можно определить по правилу правой руки: если правую руку расположить вдоль проводника так, чтобы перпендикулярная составляющая магнитной индукции входила в ладонь, а отогнутый большой палец показывал направление движения проводника, то четыре вытянутых пальца укажут направление индукционного тока в проводнике (рис. 184.4).
Если угол α между направлениями скорости «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover»«mi»v«/mi»«mo»§#8594;«/mo»«/mover»«/math» движения проводника и индукции «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover»«mi»B«/mi»«mo»§#8594;«/mo»«/mover»«/math» магнитного поля не равен 90°, то ЭДС индукции, возникающая в прямолинейном проводнике, поступательно движущемся в однородном магнитном поле, прямо пропорциональна модулю индукции магнитного поля, длине активной части проводника (части, которая находится в магнитном поле), модулю скорости движения проводника и синусу угла между направлениями магнитной индукции поля и скорости проводника:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨script¨»E«/mi»«mi»§#1080;§#1085;§#1076;«/mi»«/msub»«mo»=«/mo»«mi»B«/mi»«mi»l«/mi»«mi»v«/mi»«mi»sin§#945;«/mi»«mo».«/mo»«/math»

1. В чём отличие электростатического поля от вихревого электрического поля?
2. Что определяет ЭДС индукции, возникающую в прямолинейном проводнике, поступательно движущемся в стационарном магнитном поле?
3. От чего зависит ЭДС индукции, возникающая в прямолинейном проводнике, который поступательно движется в неизменяющемся со временем магнитном поле?