Физика. 11 класс

При движении материальной точки (МТ) по окружности радиусом R с постоянной угловой скоростью ω угол поворота φ радиус-вектора МТ изменяется со временем по закону  Центростремительное ускорение МТ направлено к центру окружности и его модуль равен

Результаты экспериментов показывают, что для возникновения и существования механических колебаний необходимо выполнение определенных условий. Прежде всего, при выведении (например, при малом смещении) тела из положения равновесия в системе должна возникать результирующая сила, стремящаяся возвратить тело в положение равновесия. Кроме того, в системе должно быть достаточно малое трение, поскольку в противном случае колебания быстро затухнут вследствие потери энергии или даже могут не возникнуть вообще. 

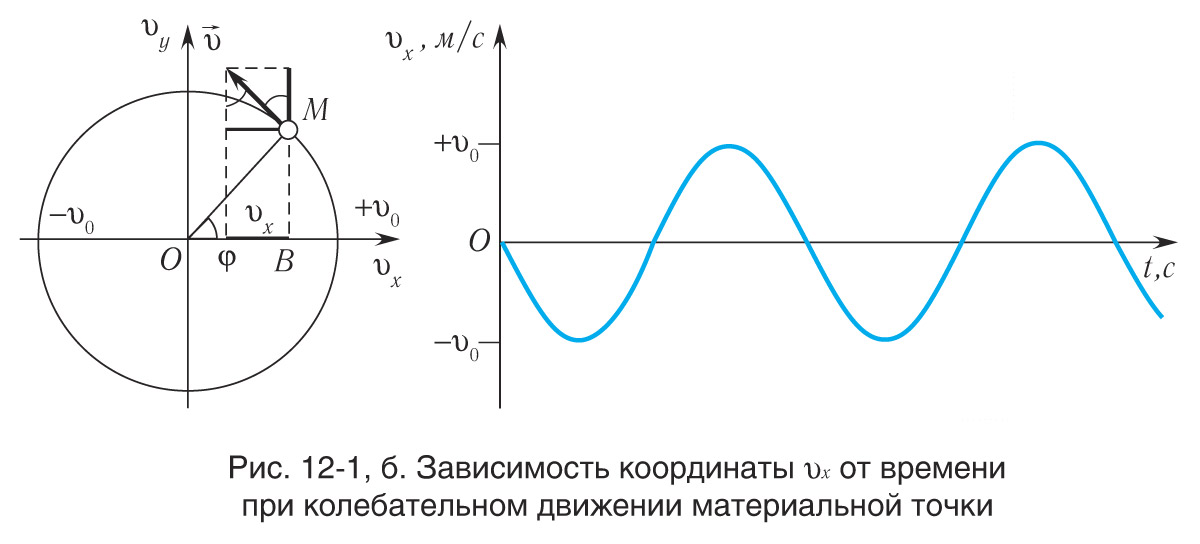
Рассмотрим изученный вами в 9-м классе случай периодического движения — равномерное вращение тела по окружности. Будем считать тело материальной точкой (МТ) и оно вращается в плоскости  по окружности радиусом R с линейной скоростью  (см. рис. 12-1, а). Пусть рассматриваемое движение происходит против хода часовой стрелки. Выберем оси O_x и O_y , как показано на рис. 12-1, а. 

Если в начальный момент времени  материальная точка находилась в положении , то через промежуток времени  она окажется в некотором положении M. Спроецируем на ось О_х  радиус-вектор  движущейся точки, ее линейную скорость  и центростремительное ускорение .

Проекция радиус-вектора  на ось О_х является его координатой х (точка B). Она определяет смещение материальной точки от центра окружности O вдоль оси  О_х (рис. 12-1, а).

Поскольку при равномерном вращении точки M по окружности ее координата (смещение) x будет периодически изменяться от  до  , то можно сказать, что точка B совершает колебательное движение вдоль оси О_х, а ее координата x является координатой колеблющейся точки.

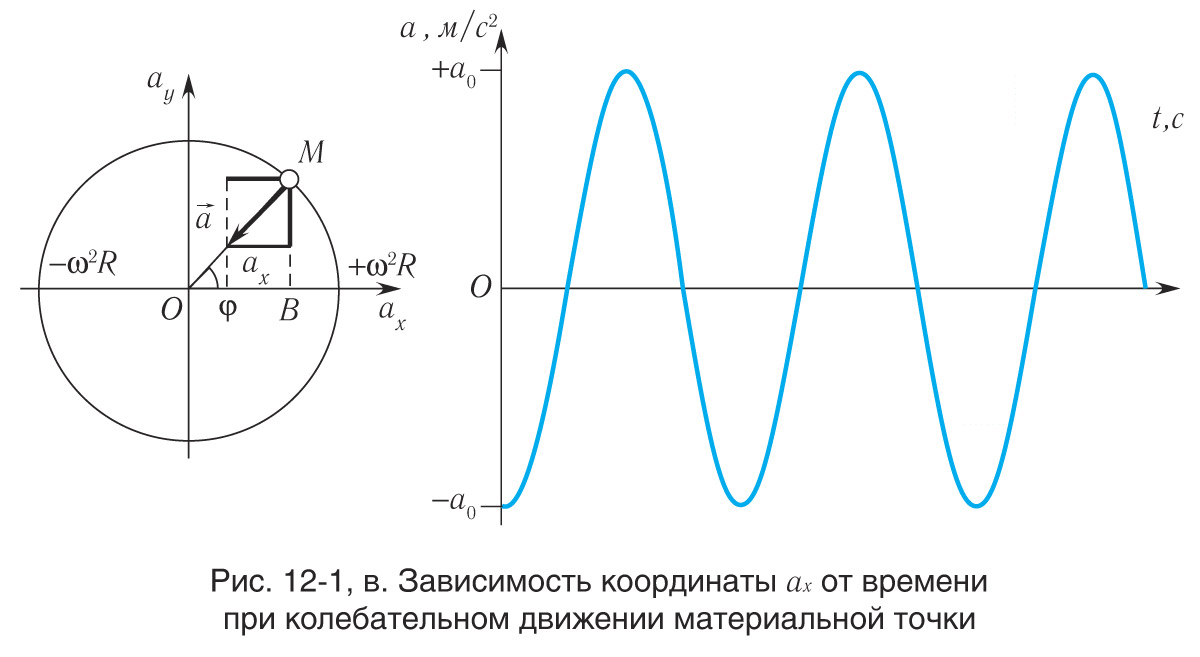
Соответственно, проекция линейной скорости  материальной точки M на ось О_х является проекцией скорости  точки B и периодически изменяется от  до  (см. рис. 12-1, б). Проекция центростремительного ускорения МТ   на ось Ох  (см. рис. 12-1, в) является проекцией ускорения  точки B , которое также периодически изменяется от  до .  

Радиус-вектор  за промежуток времени  повернулся на угол  (см. рис. 12-1, а). При равномерном вращении точки по окружности ее линейная скорость  направлена по касательной (см. рис. 12-1, б), а центростремительное ускорение  — к центру окружности (см. рис. 12-1, в). Таким образом:

,  , .

С учетом того что модуль линейной скорости v₀=ωR и модуль центростремительного ускорения  и  , выполняются соотношения:

, .

где T — период вращения тела по окружности.

Если в момент времени  материальная точка находилась в точке , то координату x, проекции скорости v_x и ускорения α_x точки B в любой момент времени можно определить по формулам:

,  ,

Поскольку функции  периодические, то через промежуток времени равный периоду T , по истечении которого угол  изменится на , все характеристики движения точки B вдоль оси  (координата, проекции скорости и ускорения) примут прежние значения (см. таблицу 1-1, рис. 12-1), т. е. значения характеристик периодически повторяются.

Точка B в течение этого промежутка времени дважды проходит через начало координат, двигаясь в противоположных направлениях вдоль оси  (рис. 12-2). Как отмечалось выше, повторяемость — основной признак периодического движения.

Таблица 1-1. Координата x, проекции скорости vx и ускорения ax МТ, движущейся по окружности, в разные моменты времени
t	x	vx	ax
0	R	O	- a0
	0	- vo	0
	- R	0	a0
	0	v0	0
T	R	0	- a0

Обратим внимание на то, что проекция ускорения   точки B (см. рис. 12-1 а, в) в любой момент времени пропорциональна смещению (координате)   и противоположна ему по знаку:

.

Перепишем данное соотношение в виде :

.

(1)

Следовательно, колебания, описываемые уравнением (1), являются гармоническими, так как их решениями являются функции синуса или косинуса. Уравнение (1) называется уравнением гармонических колебаний.  Система, совершающая такие колебания, — гармонической колебательной системой или гармоническим осциллятором (от лат. оscillo — качаюсь).

Уравнению гармонических колебаний соответствуют зависимости (5) или (6) (см. § 1), называемые кинематическим законом движения при гармонических колебаниях.

При рассмотрении колебаний важное значение имеет величина, стоящая под знаком синуса или косинуса в (2) и (3), называемая фазой колебаний. Таким образом,  фаза (от греч.  (фазис) — появление, момент явления)  — аргумент периодической функции, определяющий значение физической величины в любой момент времени t . Она определяет состояние колебательной системы (координаты, скорости, ускорения) в любой момент времени при заданной частоте и амплитуде. Единицей фазы является радиан (1 рад);

 — начальная фаза, которая определяет состояние колебательной системы в начальный момент времени ().

Амплитуда колебаний A и начальная фаза  определяются не свойствами самой системы, а тем способом, каким в системе вызваны колебания. Так, колебания можно возбудить отклонением от положения равновесия, а можно — толчком из положения равновесия.

Заметим, что точно также как мы рассматривали изменение координаты  x вращающегося по окружности тела M, можно рассматривать и изменение его координаты y (точка C) (см. рис. 12-1, а). Следовательно, точка C будет совершать гармонические колебания вдоль оси .

Таким образом, равномерное вращение тела по окружности можно рассматривать как наложение двух одинаковых по амплитуде гармонических колебаний, которые происходят одновременно в двух взаимно перпендикулярных направлениях.