§ 18. Сартаванне аднамернага масіву

18.5 . Хуткае сартаванне

Разгледзім яшчэ адзін алгарытм сартавання, які з’яўляецца істотным паляпшэннем алгарытму сартавання абменам. Сартаванне абменам з’яўляецца адным з самых неэфектыўных алгарытмаў сартавання. Аднак удасканалены алгарытм дазваляе атрымаць вынік нашмат хутчэй, таму яго вынаходнік Чарльз Хоар назваў гэты алгарытм хуткім сартаваннем (quicksort). Высокая прадукцыйнасць дасягаецца за кошт таго, што адбываецца абмен элементаў на вялікіх адлегласцях.

У масіве выбіраецца некаторы элемент, які называецца апорным. Для астатніх элементаў выконваюцца перастаноўкі такім чынам, каб злева ад апорнага знаходзіліся элементы, не большыя за яго, а справа — не меншыя. Тым самым масіў разбіваецца на дзве часткі:

    • не адсартаваныя элементы злева ад апорнага элемента;
    • не адсартаваныя элементы справа ад апорнага элемента.

У далейшым для кожнай часткі дзеянні паўтараюцца. Трэба заўважыць, што канчатковая пазіцыя апорнага элемента неабавязкова супадае з яго пазіцыяй да перастановак элементаў.

Разгледзім яе работу на тым жа масіве а = {9, 6 0, 2, 7, 3, 1, 5} (прыклад 18.14).

Фармальнае апісанне алгарытму:

  1. Завядзём два паказальнікі: левы і правы, якія дазволяць перамяшчацца па элементах масіву з пачатку і з канца.
  2.  У якасці апорнага элемента выберам элемент, які стаіць на сярэднім месцы.
  3.  Злева ад апорнага элемента знойдзем не меншы, а справа — не большы, чым апорны, і памяняем іх месцамі.
  4.  Абмен элементаў выконваем, пакуль паказальнік з левай часткі не стане большым за паказальнік з правай часткі.
  5.  Рэкурсіўна апрацоўваем 2 часткі масіву: ад пачатку да значэння правага паказальніка і ад значэння левага паказальніка да канца

Рэкурсіўная функцыя хуткага сартавання прыведзена ў прыкладзе 18.15.

У горшым выпадку алгарытм патрабуе каля n2 аперацый параўнання і столькі ж перастановак элементаў у масіве. Аднак такія выпадкі сустракаюцца нячаста (прыклад 18.16). У сярэднім, калі пры кожным рэкурсіўным выкліку масіў дзеліцца на дзве амаль роўныя часткі, то колькасць патрэбных аперацый будзе парадку nk, дзе значэнне k вызначаецца з роўнасці 2k = n. Значэнне k таксама вызначае памер дадатковай памяці для захоўвання стэка рэкурсіўных выклікаў.

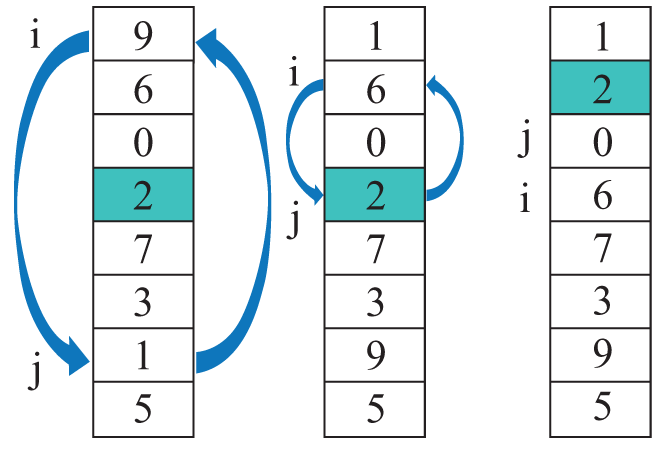
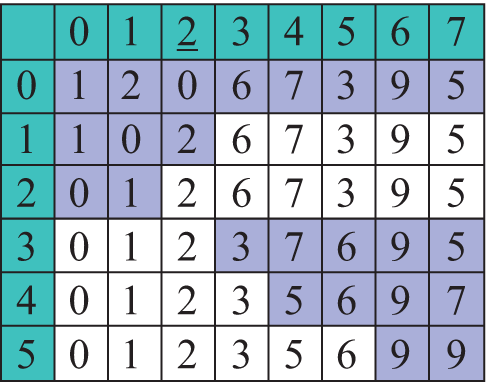
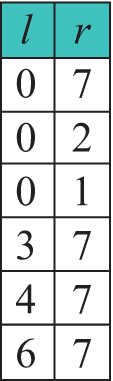
Прыклад 18.14. Хуткае сартаванне. Першы праход па масіве.

Пераменныя i і j — індэксы элементаў, якія падлягаюць абмену. Спачатку i = l = 0, j = r = 7 (пераменныяl і r — левая і правая межы апрацоўваемай часткі масіву). У канцы i = 3, j = 2 (i > j), таму абмены больш не выконваюцца. Далей функцыя працуе на падмасівах з межамі [0, 2] і [3,7].

Далейшыя этапы работы алгарытму:

   

Прыклад 18.15. Функцыя хуткага сартавання.

void quicksort(vector <int> &d, int l, int r) {

  int pivot = d[(l + r) / 2];

  int i = l, j = r;

  while (i <= j) {

    while (d[i] < pivot)

      i++;

    while (d[j] > pivot)

      j--;

    if (i <= j) {

      swap (d[i], d[j]);

      i++;

      j--;

    }

  }

  if (l < j)

    quicksort(d, l, j);

  if (i < r)

    quicksort(d, i, r);

}

У ранніх рэалізацыях хуткага сартавання, як правіла, апорным выбіраўся першы элемент. Такі выбар памяншаў прадукцыйнасць на адсартаваных масівах. Для паляпшэння эфектыўнасці можа выбірацца сярэдні, выпадковы элемент ці (для вялікіх масіваў) медыяна1 першага, сярэдняга і апошняга элементаў

Прыклад 18.16. Прыклады сітуацый, калі хуткае сартаванне не эфектыўнае:

  • калі яно ўжываецца для сартавання ўжо адсартаваных масіваў;
  • калі пасля абменаў атрымліваецца, што адзін з падмасіваў для новага рэкурсіўнага выкліку складаецца з аднаго элемента, а іншы — з n – 1 элемента;
  • калі колькасць элементаў малая (n < 32).

Рэкурсіўныя выклікі з’яўляюцца затратнымі аперацыямі, і для невялікіх масіваў іх колькасць будзе блізай да колькасці элементаў. Таму ў выпадку невялікіх аб’ёмаў даных  выкарыстоўваюць нерэкурсіўныя метады сартавання, напрыклад сартаванне ўстаўкамі ці выбарам.

*У матэматыцы для вызначэння ліку  k(2k = n) карыстаюцца функцыяй  log[2]. Алгарытм хуткага сартавання ў сярэднім выкарыстоўвае каля nlogn  параўнанняў і абменаў[3], а таксама каля logn  дадатковай памяці.

[1] Медыянай трох розных значэнняў будзе тое, якое  не роўна ні мінімальнаму, ні максімальнаму. Напрыклад, для значэнняў 3, 100 і 25 медыянай будзе 25.

[2] Калі 2k = n, то log2n = k.

[3] Кормен, Т. Алгоритмы: построение и анализ / Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн., 3-е издание. — М.: «Вильямс», 2013.