Фізіка. 11 клас

Якія з’явы назіраюцца пры адбіцці святла ад мяжы падзелу двух асяроддзяў? Як адбываецца адбіццё святла (мал. 101)? Як можна кіраваць светлавым праменем?

Для вывучэння ўласцівасцей электрамагнітных хваль неабходна ведаць заканамернасці як іх распаўсюджвання ў аднародным асяроддзі, так і адбіцця і праламлення на мяжы падзелу двух асяроддзяў.

На падставе хвалевай тэорыі можна рашаць задачы аб распаўсюджванні святла як у аднародным асяроддзі, так і праз любую аптычную сістэму, якая ўяўляе сабой набор розных аптычных элементаў, абмежаваных паверхнямі і дыяфрагмамі. Аднак разлік і канструяванне шматлікіх аптычных прыбораў і прылад, пачынаючы ад найпрасцейшых луп і канчаючы гіганцкімі тэлескопамі, можна зрабіць значна больш простым шляхам, з дапамогай законаў геаметрычнай оптыкі

Геаметрычнай оптыкай называюць раздзел оптыкі, у якім вывучаюцца законы распаўсюджвання аптычнага выпраменьвання на падставе ўяўлення аб светлавых праменях. У геаметрычнай оптыцы хвалевая прырода святла не ўлічваецца. Дамовімся паказваць светлавыя прамені графічна з дапамогай геаметрычных праменяў. Геаметрычнаму праменю на практыцы адпавядае тонкі светлавы пучок, які атрымліваецца пры прапусканні светлавога выпраменьвання, што ідзе ад аддаленай крыніцы, праз адтуліну (дыяфрагму) у экране (мал. 102). 

Такім чынам, трэба адрозніваць геаметрычны прамень (матэматычнае паняцце) і светлавы пучок (матэрыяльны аб’ект), атрыманы ад крыніцы святла.

Ужо ў пачатковыя перыяды аптычных даследаванняў былі эксперыментальна вызначаны чатыры асноўныя законы геаметрычнай оптыкі:

- закон прамалінейнага распаў-сюджвання святла (мал. 102, 103);

- закон незалежнасці светлавых праменяў;

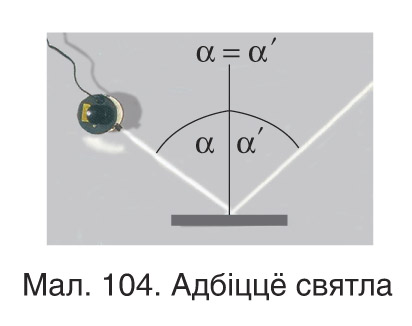
- закон адбіцця светлавых праменяў (мал. 104);

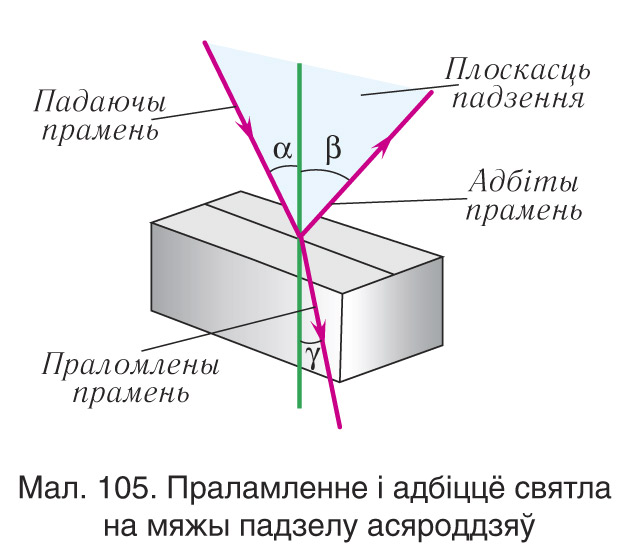
- закон праламлення светлавых праменяў (мал. 105).

У законе прамалінейнага рас­паўсюджвання святла, законах адбіцця і праламлення святла вы­карыстоўваліся паняцці «светлавы пучок» і «светлавы прамень», прычым апошні разглядаўся як бясконца тонкі пучок. Светлавы па­ток можна падзяліць на асобныя светлавыя пучкі пры дапамозе дыяфрагм (гл. мал. 103).

Закон адбіцця святла

Разгледзім працэсы, якія адбываюцца пры падзенні плоскай хвалі на плоскую паверхню падзелу аднародных ізатропных і празрыстых асяроддзяў пры ўмове, што памеры паверхні падзелу нашмат большыя за даўжыню хвалі падаючага выпраменьвання.

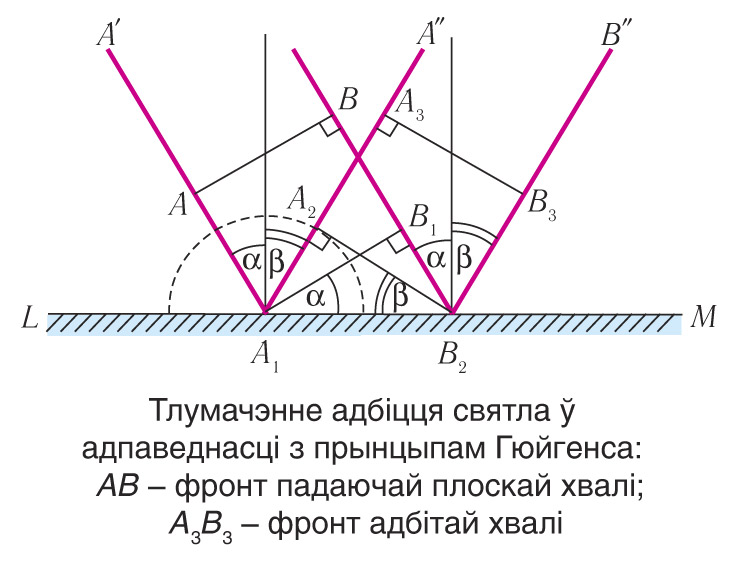
Няхай на плоскую паверхню падзелу LM двух асяроддзяў падае плоская хваля, фронт якой  (мал. 105-1). Калі вугал падзення α адрозны ад нуля, то розныя пункты фронта AB хвалі дасягнуць мяжы падзелу LM неадначасова.

Згодна з прынцыпам Гюйгенса, пункт A₁ якога фронт хвалі дасягне раней за ўсё (гл. мал. 105-1), стане крыніцай другасных хваль. Другасныя хвалі будуць распаўсюджвацца са скорасцю v і за прамежак часу , за які пункт фронта B₁ дасягне мяжы падзелу двух асяроддзяў (пункта B₂), другасныя хвалі з пункта A₁, пройдуць адлегласць А1А2=vΔt

Падаючая і ўтвараемыя другасныя хвалі распаўсюджваюцца ў адным і тым жа асяроддзі, таму іх скорасці аднолькавыя, і яны пройдуць аднолькавыя адлегласці . Датычная, праведзеная з пункта B₂  да паўакружнасці радыусам А1А2=vΔt, з’яўляецца агібаючай другасных хваль і дае становішча фронту хвалі праз прамежак часу Δt. Затым ён перамяшчаецца ў напрамку . З пабудовы вынікае, што  і . З улікам азначэнняў вугла падзення α і вугла адбіцця β знаходзім, што вугал  і  як вуглы з узаемна перпендыкулярнымі старанамі. Такім чынам, вугал адбіцця роўны вуглу падзення (β=α).

Акрамя таго, як паказваюць эксперыменты, прамень падаючы, прамень адбіты і перпендыкуляр да мяжы падзелу двух асяроддзяў, праведзены ў пункце падзення праменя, ляжаць у адной плоскасці (гл. мал. 105-1).

Такім чынам, зыходзячы з хвалевай тэорыі святла, на падставе прынцыпу Гюйгенса атрыманы закон адбіцця святла.

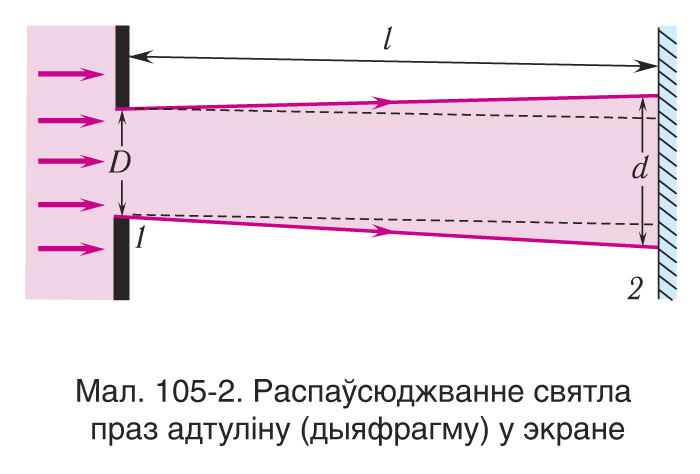
Светлавыя пучкі атрымліваюць пры прапусканні светлавога выпраменьвання, што ідзе ад аддаленай крыніцы, праз адтуліну (дыяфрагму) у экране (мал. 105-2). Эксперыменты паказваюць, што калі дыяметр  D значна большы за даўжыню светлавой хвалі  λ (D>>λ), і адлегалсць l ад адтуліны да экрана вялікая ў параўнанні з памерам дыяфрагмы (l>>D), то пучок, які выходзіць з дыяфрагмы, з'яўляецца паралельным. Для яго на не занадта вялікіх адлегласцях l ад экрана выконваецца няроўнасць

Калі ж дыяметр дыяфрагмы або памеры прадмета аказваюцца параўнальнымі з даўжынёй светлавой хвалі, то светлавы пучок, што выходзіць, становіцца разыходным, святло трапляе ў абсяг геаметрычнага ценю, адбываецца дыфракцыя святла, г. зн. выяўляецца хвалевы характар светлавога выпраменьвання. Трэба адзначыць, што дыфракцыя будзе назірацца на вельмі вялікіх адлегласцях ад экрана  () нават пры дыяметры светлавой адтуліны D>>λ.

Такім чынам, трэба адрозніваць геаметрычны прамень (матэматычнае паняцце) і светлавы пучок (матэрыяльны аб'ект), які атрымліваецца ад крыніцы святла. Прамень — гэта напрамак, перпендыкулярны да фронту хвалі, у якім яна пераносіць энергію.

Прамені, якія выходзяць з ад­наго пункта, называюць разы­ходнымі, а прамені, якія збіраюцца ў адным пункце, — сыходнымі (мал. 106). 

Як бачна з малюнка 106, сферычнай хвалі адпавядае разыходны пучок светлавых праменяў, а плоскай — паралельны пучок.

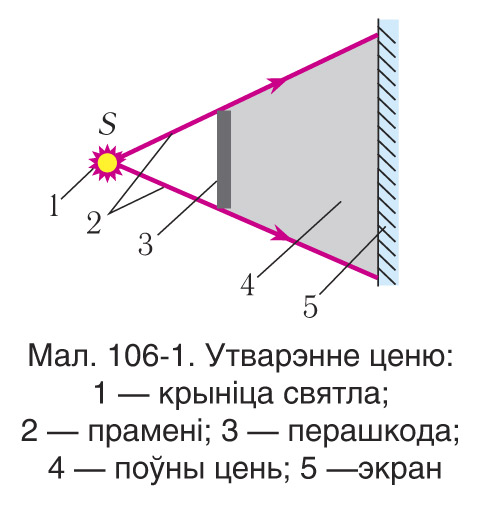
Доказам закону прамалінейнага распаўсюджвання святла служыць утварэнне поўнага ценю і паўценю, геаметрычна падобных да перашкод. Крыніца дае поўны цень (мал. 106-1), калі яе памеры значна меншыя за адлегласць да перашкоды, якая адкідае цень. Такую крыніцу прынята называць кропкавай. Падкрэслім, што кропкавая крыніца святла з'яўляецца ідэалізацыяй, падобна да матэрыяльнага пункта ў механіцы

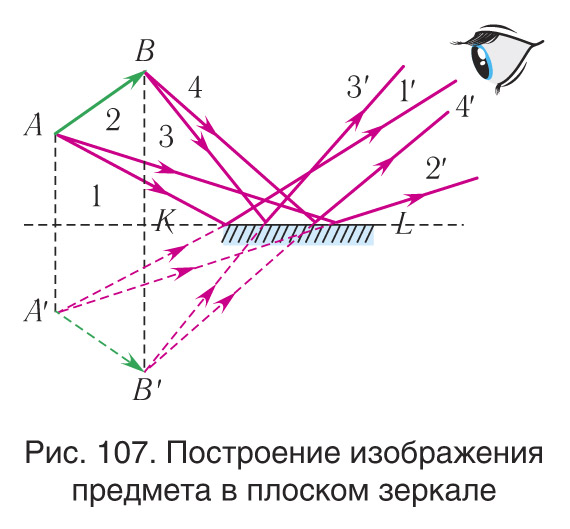
Выкарыстаўшы закон адбіцця, мож­на пабудаваць відарыс прадмета АВ у плоскім люстры (мал. 107), што ўяў­ляе сабой плоскую адбіваючую паверхню. Пабудаваўшы ход праменяў 1 і 2 ад пункта А пасля адбіцця ад люстра KL, прадоўжым іх да скрыжавання ў пункце A′ Аналагічныя пабудовы зробім для пункта В. Воку назіральніка будзе здавацца, што прамені выйшлі з пунктаў  A′ і B′ г. зн. з крайніх пунктаў відарыса A′B′   прадмета АВ.

У оптыцы відарыс называецца сапраўдным, калі ён утвораны самімі прамянямі (г. зн. у дадзены пункт паступае светлавая энергія). Калі ж відарыс утвораны не самімі прамянямі, а іх прадаўжэннямі, то кажуць, што відарыс уяўны (светлавая энергія не паступае ў дадзены пункт). 

Відарыс называецца прамым, калі ён арыентаваны таксама, як прадмет. Калі ж відарыс перавернуты, то яго называюць адваротным або перавернутым.

Такім чынам, відарыс прадмета ў плоскім люстры — уяўны прамы, у натуральную велічыню. Ён сіметрычны прадмету адносна плоскасці люстра і знаходзіцца на такой жа адлегласці за плоскасцю люстра, як і сам прадмет (гл. мал. 107).

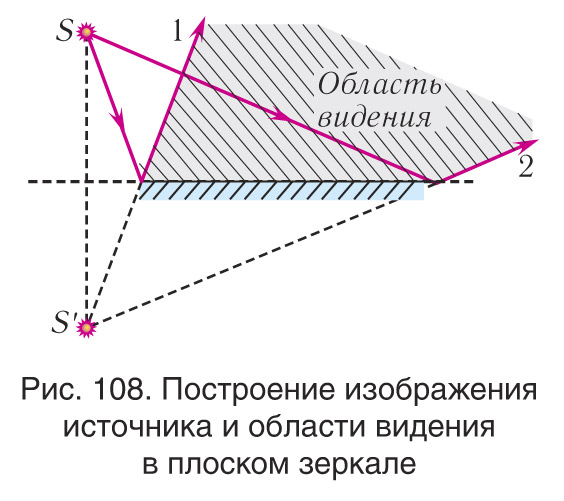
На малюнку 108 паказаны прыклад пабудовы абсягу бачання крыніцы S у плоскім люстры. Для яго атрымання неабходна пабудаваць ход пра­меняў 1 і 2, накіраваных на краі люстра. Абсяг (заштрыхаваны) паміж адбітымі праменямі і дае абсяг, знаходзячыся ў якім можна ўбачыць крыніцу.