§ 15. Інтэрферэнцыя святла
Прыклад рашэння задачы
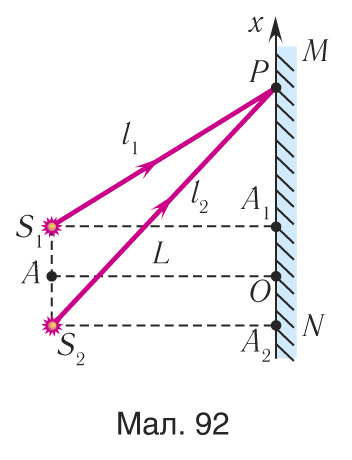
Вызначыце становішчы максімумаў і мінімумаў інтэрферэнцыйнай карціны на экране, які знаходзіцца на адлегласці L = AO = 2,0 м ад дзвюх аднолькавых кагерэнтных крыніц святла S1 і S2, размешчаных у вакууме на адлегласці d = 5,0 мм адна ад адной (мал. 92). Даўжыня хвалі выпраменьвання крыніц λ = 600 нм. Знайдзіце адлегласць Δx паміж суседнімі максімумамі.
L = 2,0 м,
λ = 600 нм =6,00·10-7 м.
Рашэнне:
Да некаторага пункта P на экране кожная з хваль праходзіць розны шлях l1 і l2. Максімум і мінімум будуць назірацца пры выкананні ўмоў, адпаведна:
δ = l2 - l1 = mλ,
З трохвугольнікаў ΔS1PA1 i ΔS2PA2, па тэараме Піфагора знаходзім:
| (1) | ||
| (2) |
дзе xm — каардыната пункта P.
Адкуль, адняўшы ад суадносіны (2) суадносіну (1), атрымаем:
З улікам таго, што d << L i l1 + l2 2L знаходзім:
З умовы максімумаў вынікае:
| |
Тады адлегласць ад цэнтра экрана да m-й светлай паласы знаходзіцца з суадносіны:
З умовы для мінімумаў знаходзім становішча цёмных палос
Адкуль:
Адлегласць паміж суседнімі максімумамі:
З атрыманай формулы бачна, што адлегласць Δx павялічваецца пры памяншэнні адлегласці d паміж кагерэнтнымі крыніцамі.
Адказ: