Физика. 11 класс

Изменение представлений о свойствах пространства и времени повлекло за собой появление новых взглядов на связь энергии тела с его массой. В чем суть знаменитой формулы Эйнштейна ? Где она находит свое применение?

Сформулированные Эйнштейном постулаты, положенные в основу специальной теории относительности (СТО), привели к пересмотру им взглядов на классическую (ньютоновскую) механику. Классические выражения для импульса и энергии были изменены для новой, уточненной формы записи законов сохранения импульса и энергии. Таким образом, теория относительности потребовала пересмотра и уточнения законов механики, вид которых оставался неизменным со времен Ньютона.

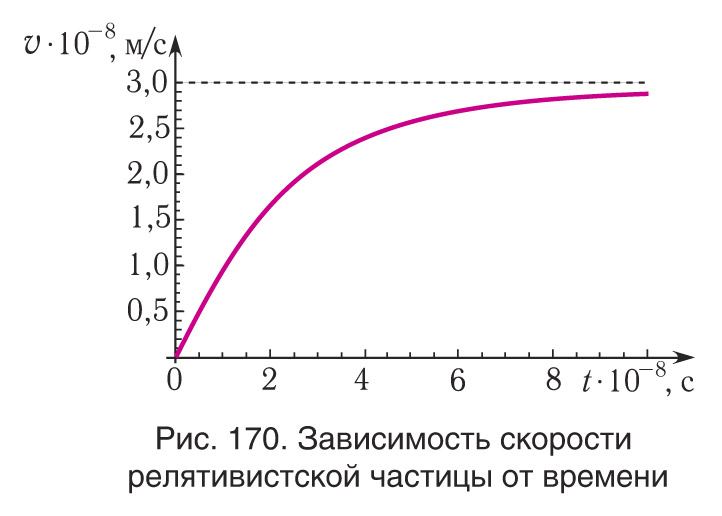
Необходимость изменения динамики очевидна хотя бы из того, что согласно законам Ньютона любое тело можно в принципе разогнать до любой скорости. Приложим к покоящемуся телу массой m  постоянную силу . Используя второй закон Ньютона, найдем, что к моменту времени  t  тело приобретет скорость . Следовательно, в рамках классической механики при скорость тела  v  превзошла бы скорость света c, что противоречит результатам экспериментов и основным положениям СТО. Зависимость скорости v тела от времени t в релятивистском случае приведена на рисунке 170.

Какие же соотношения динамики оказалось необходимым изменить в рамках СТО, а какие остались неизменными?

Сохранили свой вид законы изменения импульса и энергии тела:

,

(1)

где  A — работа, совершенная силой .

Изменились соотношения, выражающие зависимость импульса и энергии тела от его скорости:

,.

Уравнения динамики следует изменить так, чтобы они оставались неизменными при переходе от одной инерциальной системы отсчета к другой согласно принципу относительности. В случае малых скоростей (v << c) уравнения релятивистской динамики должны переходить в классические, ибо в этой области их справедливость подтверждается в многочисленных экспериментах.

В СТО эффективно применяется фундаментальное динамическое соотношение, связывающее полную энергию E и импульс  свободной частицы массой m, движущейся со скоростью :

(1-1)

причем масса m здесь та же самая величина,  что и в классической механике.

Выражение для импульса  в классической механике не удовлетворяет принципам СТО, законам сохранения энергии и импульса, а также соотношению (1-1). Поэтому в СТО релятивистский импульс определяется новым выражением:

.

(1-2)

Особенно важно отметить, что формулы (1-1) и (1-2) описывают движение частиц во всем интервале возможных скоростей:  . При движении со скоростью распространения света (v = c) модуль импульса и энергия связаны соотношением:

.

(1-3)

Подставив  выражение (1-3) в формулу (1-1), получим:

.

Откуда следует, что масса частицы, движущейся со скоростью света в вакууме равна нулю.

Для частиц с ненулевой массой выразим энергию и импульс через массу и скорость. Подставим выражение (1-2) в (1-1):

.

Отсюда получим:

,

(1-4)

где называется лоренцевским множителем.

Подставляя выражение (1-4) в (1-2), имеем:

.

(1-5)

Таким образом, для тел, движущихся со скоростями близкими к скорости распространения света в вакууме, их энергия и импульс определяются соотношениями (1-4) и (1-5).

Основное уравнение релятивистской динамики по-прежнему записывается в виде:

,

(1-6)

где:

.

Важнейшим отличием СТО от классической механики является то, что энергия тела не обращается в нуль, даже когда оно покоится (v = 0). В этом случае энергия покоя E₀ тела пропорциональна его массе:

.

(2)

Таким образом, в покоящемся теле таится огромный запас энергии. Трудно переоценить практическое значение этой несложной формулы, поскольку именно она указала на взаимосвязь энергии и массы вещества. Человечество узнало о возможности получения энергии из вещества. На этой формуле основана вся энергетика, в которой энергия покоя топлива переходит в другие виды энергии.

Из равенства (2) следует, что изменение энергии покоя тела на  связано с изменением его массы на  , где:

.

(3)

Утверждение о том, что энергия покоя пропорциональна массе, а изменение энергии покоя связано с изменением массы, называют законом взаимосвязи массы и энергии. 

Трудно переоценить практическое значение этого закона для современной энергетики. Из него следует, что тело массой  m = 1,0 г обладает энергией покоя:

.

Эта энергия эквивалентна энергии, выделяющейся при сгорании 2000 тонн нефти! Так, благодаря прогрессу физики, в 1905 году человечество узнало о практически «неисчерпаемых» запасах энергии, содержащихся в любом веществе.

Формула (3) применима ко всем явлениям, в которых изменяется внутренняя энергия вещества. При процессах, происходящих на атомно-молекулярном уровне, изменения массы крайне малы. Так, при полном превращении льда в воду относительное изменение массы  , при нагревании на  железного бруска  . При химических реакциях относительное изменение массы несколько выше. Например, при сгорании метана в кислороде  . Для ядерных реакций ситуация существенно иная. Для них характерны величины , в десятки миллионов раз бóльшие, чем для химических реакций.

Согласно СТО масса частицы является мерой энергии, содержащейся в покоящейся частице, т.е. энергии покоя. Это свойство массы было неизвестно в классической механике.

Масса элементарной частицы является одной из ее важнейших характеристик, которую стараются измерить с наибольшей точностью. Ее определяют из формулы (1-1):

.

(3-1)

посредством измерения энергии  и модуля импульса частицы.

В СТО, также как и в классической механике, масса изолированной системы тел сохраняется, т.е. не изменяется со временем.

Кинетическую энергию E_к определяют как разность полной энергии E и энергии покоя E₀:

(3-2)

В случае, когда скорость частицы стремится к скорости распространения света, кинетическая энергия частицы стремится к бесконечности. Это означает, что частицу, обладающую некоторой массой, невозможно разогнать до скорости распространения света.

Полученные формулы применимы к любому сложному телу, состоящему из многих частиц, причем под массой m необходимо понимать полную массу тела, а под скоростью  — его скорость движения как целого. Энергия покоящегося тела содержит в себе, помимо энергий покоя входящих в него частиц, также кинетическую энергию частиц и энергию их взаимодействия.

При малых скоростях (v << c), т.е.  и для релятивистского множителя γ можно использовать приближенное соотношение  при x << 1. (Можете проверить это соотношение численно на калькуляторе, например при x = 0,1 ; 0,05).

Тогда:

.

(3-3)

Выражение для релятивистского импульса (1-5) и релятивистской кинетической энергии (3-2) переходят в классические, используемые в классической механике:

, .

Как видим, теория Эйнштейна не противоречит теории Ньютона. Более того, она «содержит» ее в себе как частный случай при малых скоростях.

Согласно принципу соответствия любая новая физическая теория, претендующая на более глубокое описание физических явлений (соответственно и на более широкую область применимости), должна включать в себя классическую (Ньютоновскую) теорию как предельный случай.

Этот принцип выражает требование преемственности знаний. В соответствии с ним, новая теория должна включать в себя предшествующую ей теорию и указывать пределы применимости ее идей и методов расчета. При скоростях движения v << c  законы релятивистской механики переходят в законы классической механики. На практике все формулы СТО переходят в формулы классической механики, в предположении, что .