§ 19. Бінарны пошук у адсартаваным масіве

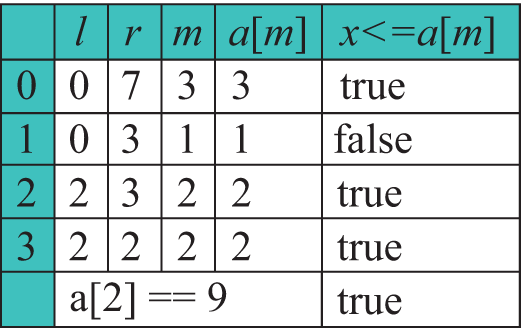
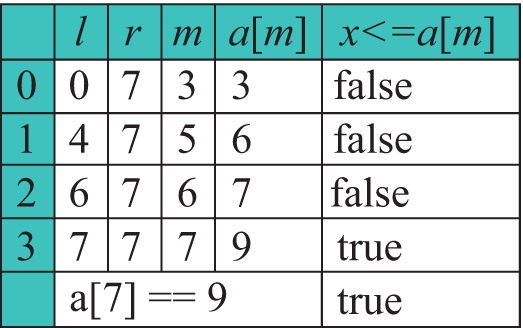
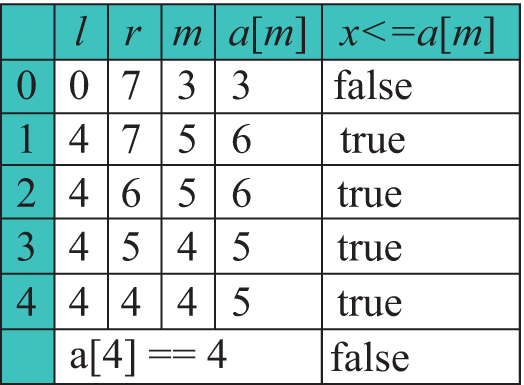
У папярэднім параграфе гаварылася пра тое, што ў адсартаваным масіве пошук элемента можна ажыццяўляць, не праглядаючы ўвесь масіў.

Для таго каб зразумець, як гэта можна зрабіць, разгледзім наступную задачу. Выкажам здагадку, што хтосьці загадаў цэлы лік ад 1 да 100. Каб адгадаць лік, можна задаваць пытанні, адказам на якія будзе «так» ці «не». Адзін з варыянтаў адгадвання — гэта задаваць пытанні выгляду «Гэта 1?», «Гэта 2?» і г. д. У самым горшым выпадку прыйдзецца задаць 99 пытанняў. Гэта стратэгія лінейнага (паслядоўнага) пошуку. Тут мы не ўлічваем той факт, што лікі ад 1 да 100 размешчаны ў парадку ўзрастання. Калі задаць пытанне «Гэты лік большы за 50?», то пры адказе «так» стане зразумела, што сярод першых 50 лікаў загаданага ліку няма і яго трэба адгадваць сярод лікаў ад 50 да 100. Калі адказ «не», то з разгляду выключаюцца лікі, большыя за 50. У любым выпадку колькасць магчымых лікаў скарачаецца ў два разы. Далей, у залежнасці ад адказу, пытаемся: «Гэты лік большы за 75 (25)?» і скарачаем вобласць прагляду яшчэ ў два разы. Для наступнага пытання выбіраем лік, які стаіць у сярэдзіне астатняга прамежку лікаў.

Такім чынам, які б лік (ад 1 да 100) ні быў загаданы, адгадаць яго можна не больш чым за 7 пытанняў  (27 = 128 > 100), што істотна менш, чым 99 (вынік лінейнага пошуку).

Такі метад пошуку называецца бінарным пошукам. Сустракаюцца і іншыя назвы гэтага метаду: двайковы пошук, лагарыфмічны пошук, метад дзялення папалам, дыхатамія.

У праграміраванні такі пошук ужываюць для знаходжання элемента x у адсартаваным масіве. Пошук элемента ў масіве  
а = {0, 1, 2, 3, 5, 6, 7, 9} паказаны ў  прыклад 19.1.

Фармальнае апісанне алгарытму:

1. Вызначаем левую і правую межы прамежку пошуку (спачатаку l = 0, r = n - 1).

2. Шуканы элемент параўноўваецца з элементам масіву, як стаяць пасярэдзіне  (m = (l + r) / 2):

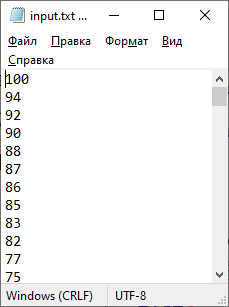
  • калі значэнне шуканага элемента не большае за сярэдні элемент, то зыходнай паслядоўнасцю лічыцца масіў ад 0 до r = m (змяняецца правая мяжа);
  • калі значэнне шуканага элемента большае за сярэдні элемент, то зыходнай паслядоўнасцю лічыцца масіў ад l = m +1 до n – 1 (змяняецца левая мяжа).

3. Для новай паслядоўнасці гэты працэс паўтараецца.

4. Працягваем дзяленне прамежку пошуку папалам да таго часу, пакуль левая мяжа пошуку меншая за правую.

Ёсць два спосабы рэалізацыі гэтага алгарытму: ітэратыўны (прыклад 19.2) і рэкурсіўны (прыклад 19.3). Функцыя вяртае значэнне true, калі элемент знойдзены, і false ў адваротным выпадку.

Калі неабходна ведаць яшчэ і месца, на якім знаходзіцца шуканы элемент, то магчымы два варыянты. У якасці значэння функцыі, якое вяртаецца, вызначыць структуру з двума палямі (bool і int). Лагічнае поле будзе служыць для вызначэння таго, знойдзены элемент ці не, а цэлалікавае будзе захоўваць індэкс знойдзенага элемента. У выпадку калі элемент не знойдзены, то значэнне другога поля будзе вызначаць месца для ўстаўкі элемента ў масіў без парушэння ўпарадкаванасці масіву (прыклад 19.4).

Іншым магчымым варыянтам для захавання індэкса знойдзенага элемента можа стаць дадатковы параметр, значэнне якога будзе перадавацца па спасылцы.

Для ацэнкі колькасці аперацый, неабходных для атрымання выніку, будзем разважаць наступным чынам. Няхай натуральны k — колькасць аперацый параўнання, якія неабходны для знаходжання элемента ва ўпарадкаваным масіве метадам дыхатаміі. Тады лік k вызначаецца з наступнай няроўнасці: n ≤ 2k, прычым k — мінімальны з усіх магчымых.

Прыклад 19.5. Дадзены лінейны адсартаваны масіў цэлых лікаў. Напісаць праграму, якая атрымае колькасць элементаў, размешчаных паміж x і y. (Мяркуецца, што такія элементы існуюць і адзіныя.) Масіў упарадкаваны ў парадку спадання. Даныя прачытаць з файла. Лікі x і y увесці з клавіятуры.

Этапы выканання заданя

I.Зыходныя даныя: пераменныя n — колькасць лікаў у масіве, a — масіў, лікі x і y.

II. Вынік: колькасць элементаў паміж  x і y.

III. Алгарытм рашэння задачы.

  1. Увод зыходных даных.
  2. Для рашэння задачы будзем выкарыстоўваць алгарытм бінарнага пошуку. Паводле ўмовы задачы масіў адсартаваны па спаданні, таму ў праграме неабходна памяняць знак параўнання: «<=» на «>=» пры параўнанні шуканага элемента з сярэднім.
  3. Вызначым пазіцыю лікаў x і y у масіве.
  4.  Адказам будзе значэнне, роўнае модулю рознасці пазіцый для лікаў x і y мінус 1.
  5. Вывад выніку

IV. Апісанне пераменных: n, x, y – int, a –  vector<int>.

Ідэі шмат якіх алгарытмаў паходзяць са звычайных жыццёвых сітуацый. Разгледзім прыклад.

У мастацкім музеі рыхтуецца змена экспазіцыі, таму карціны з некалькіх зал здымаюць і пакуюць для захоўвання. Адну з карцін павінны былі адправіць на выставу ў іншы горад, таму яе апрацавалі спецыяльным саставам, што ахоўвае ад пашкоджванняў. Гэты састаў мае пах, які не адчувае чалавек. Але ёсць прыбор, які можа ўлавіць гэты пах у памяшканні. Памылкова карціну, падрыхтаваную да выставы, упакавалі разам з іншымі. Карціны пакуль не адправілі ў сховішча, усе яны знаходзяцца ў адной зале. Як знайсці сярод усіх карцін тую, якую павінны адправіць на выставу? Самым простым (і самым працяглым па часе рашэннем) будзе паслядоўны прагляд усіх карцін у зале. Аднак такі падыход наўрад ці дапаможа сэканоміць час.

Паступім па-іншаму. Падзелім усе карціны на дзве прыкладна роўныя па колькасці часткі. Разнясём іх па дзвюх залах (паколькі карціны ўжо прыгатаваны да транспартавання, іх можна лёгка перамяшчаць). Прыбор зможа вызначыць, у якой з зал знаходзіцца карціна. У выніку такога дзеяння колькасць карцін для пошуку паменшыцца ўдвая. З тымі карцінамі, сярод якіх знаходзіцца шуканая, паступім аналагічным чынам: падзелім на 2 часткі і разнясём у розныя залы. Пры гэтым зноў колькасць карцін паменшыцца. Працягваем так да таго часу, пакуль у зале не застанецца адна карціна, на якую рэагуе прыбор.

Прыклад 19.1. Бінарны пошук элемента ў адсартаваным масіве:

x = 2

x = 9

x = 4

Бінарны пошук заснаваны на стратэгіі «падзяляй і кіруй»[1].

«Падзяляй» — задача разбіваецца на некалькі падзадач меншага памеру.

«Кіруй» — падзадачы рашаюцца (рэкурсіўна або непасрэдна).

Нарэшце рашэнні падзадач аб’ядноўваюцца, і атрымліваецца рашэнне зыходнай задачы.

Прыклад 19.2. Ітэратыўная функцыя бінарнага пошуку.

bool bin_poisk(const

vector <int> &d, int z)

{

  int l = 0;

  int r = d.size() - 1;

  while (l < r) {

    int m = (l + r ) / 2;

    if (z <= d[m])

      r = m;

    else

      l = m + 1;

  }

  if (d[r] == z)

    return true;

  else

    return false;

}

Прыклад 19.3. Рэкурсіўная функцыя бінарнага пошуку.

bool bin_poisk(const vector <int> &d, int z, int l, int r)

{

  if (d[r] == z)

    return true;

  else

    if (l < r) {

      int m = (l + r ) / 2;

      if (z <= d[m])

        bin_poisk(d, z, l, m);

      else

        bin_poisk(d, z, m + 1, r);

      }

    else

      return false;

Прыклад 19.4. Функцыя бінарнага пошуку з вяртаннем знойдзенай пазіцыі элемента.

struct rez_bin 
{
  bool rez;
  int pos;
};

rez_bin bin_poisk const vector <int> &d, int z)

{

  int l = 0;

  int r = d.size() - 1;

  while (l < r) {

    int m = (l + r ) / 2;

    if (z <= d[m])

      r = m;

    else

      l = m + 1;

  }

  if (d[r] == z)

    return {true, r};

  else

    if (d[r] < z)

      return {false, r + 1};

    else

      return {false, r};

}

Выкарыстоўваючы функцыю log, можна вылічыць лік k па наступнай формуле: begin mathsize 16px style straight k space equals space open square brackets log subscript 2 straight n close square brackets space plus space 1 comma end style дзе квадратныя дужкі абазначаюць цэлую частку ліку, што знаходзіцца ў дужках.

Прыклад 19.5.

V. Праграма:

#include <iostream>

#include <fstream>

#include <vector>

#include <cmath>

 

using namespace std;

 

struct rez_bin

{

  bool rez;

  int pos;

};

 

rez_bin bin_poisk (const vector <int> &d, int z)

{

  int l = 0;

  int r = d.size() - 1;

  while (l < r) {

    int m = (l + r ) / 2;

    if (z >= d[m])

      r = m;

    else

      l = m + 1;

  }

  if (d[r] == z)

    return {true, r};

  else

    if (d[r] < z)

      return {false, r + 1};

    else

      return {false, r};

}

 

int main()

{

  ifstream fin("input.txt");

  int n;

  fin >> n;

  vector <int> a(n);

  for (int i = 0; i < n; i++)

    fin >> a[i];

  int x, y;

  cout << "x, y" << endl;

  cin >> x >> y;

  rez_bin r1 = bin_poisk(a, x);

  rez_bin r2 = bin_poisk(a, y);

  int rez = abs(r2.pos - r1.pos) - 1;

  cout << "mezdu x i y ";

  cout << rez << " chisel";

  cout << endl;

  return 0;

}

 VI. Тэсціраванне.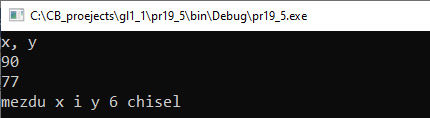


[1] Кормен, Т. Алгоритмы: построение и анализ / Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн. 3-е издание. — М.: «Вильямс», 2013.