§ 18. Сартаванне аднамернага масіву
18.2. Сартаванне выбарам
|
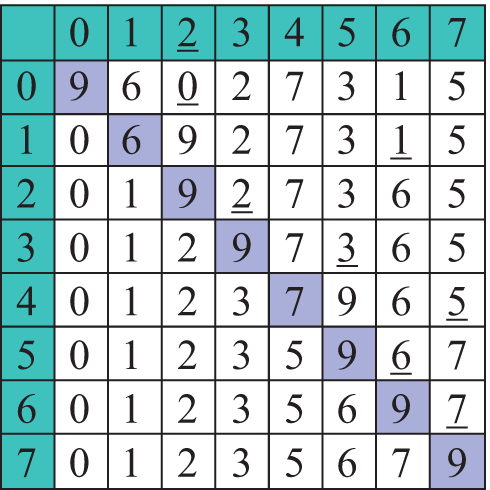
Давайце ўявім, што перад намі пастаўлена задача расставіць N лікаў па ўзрастанні. Як бы мы яе рашалі? Напэўна, прыйшлося б спачатку знайсці мінімальны з усіх лікаў і паставіць яго на першае месца ў паслядоўнасці. Затым з яшчэ неадсартаваных элементаў трэба было б зноў выбраць мінімальны элемент і паставіць яго пасля ўжо адсартаванай часткі і г. д. (прыклад 18.3) Разгледзім работу дадзенага метаду на масіве a = {9, 6, 0, 2, 7, 3, 1, 5}. Мінімальны элемент на кожным кроку падкрэслены (прыклад 18.4). Колерам вылучаны той элемент, які на бягучым кроку мяняецца месцамі з мінімальным. Ужыты метад называецца сартаванне выбарам. Назва метаду вызначаецца тым, што на кожным кроку мы знаходзім (выбіраем) мінімальны элемент з яшчэ неадсартаванай часткі масіву (прыклад 18.5). Фармальнае апісанне алгарытму. На i-м кроку (i = 0, …, n - 1) выконваем:
Палічым колькасць параўнанняў, якія прыйшлося зрабіць для ўпарадкавання масіву. На першым кроку для знаходжання максімальнага элемента неабходна (n – 1) параўнанняў, на другім — (n – 2), на трэцім (n – 3), ..., на апошнім кроку — адно параўнанне. Знойдзем суму: n – 1 + n – 2 + n – 3 ... + 1 = |
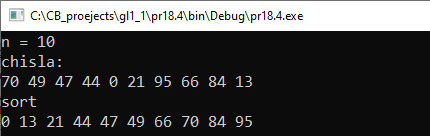
Прыклад 18.3. Дэманстрацыя сартавання лікаў на прыкладзе дзіцячай цацкі, у якой трэба выбіраць і расстаўляць лікі па сваіх месцах: Прыклад 18.4. Сартаванне масіву метадам выбару: Прыклад 18.5. Праграма алгарытму сартавання метадам выбару:
Тэсціраванне. Унутраны цыкл for з’яўляецца не чым іншым, як алгарытмам пошуку мінімальнага элемента сярод элементаў з нумарамі ад k + 1 да n – 1. Суму колькасці параўнанняў можна атрымаць зыходзячы з таго, што лікі n – 1, n – 2, … 1 утвараюць арыфметычную прагрэсію. Сума элементаў гэтай арыфметычнай прагрэсіі роўна
|