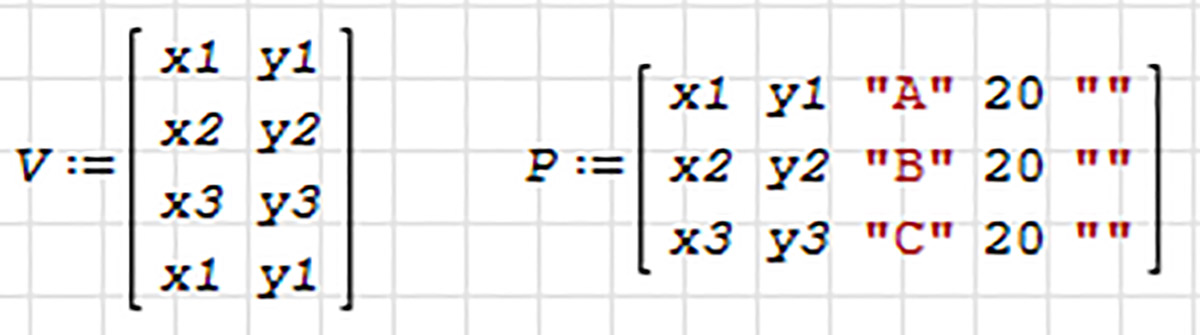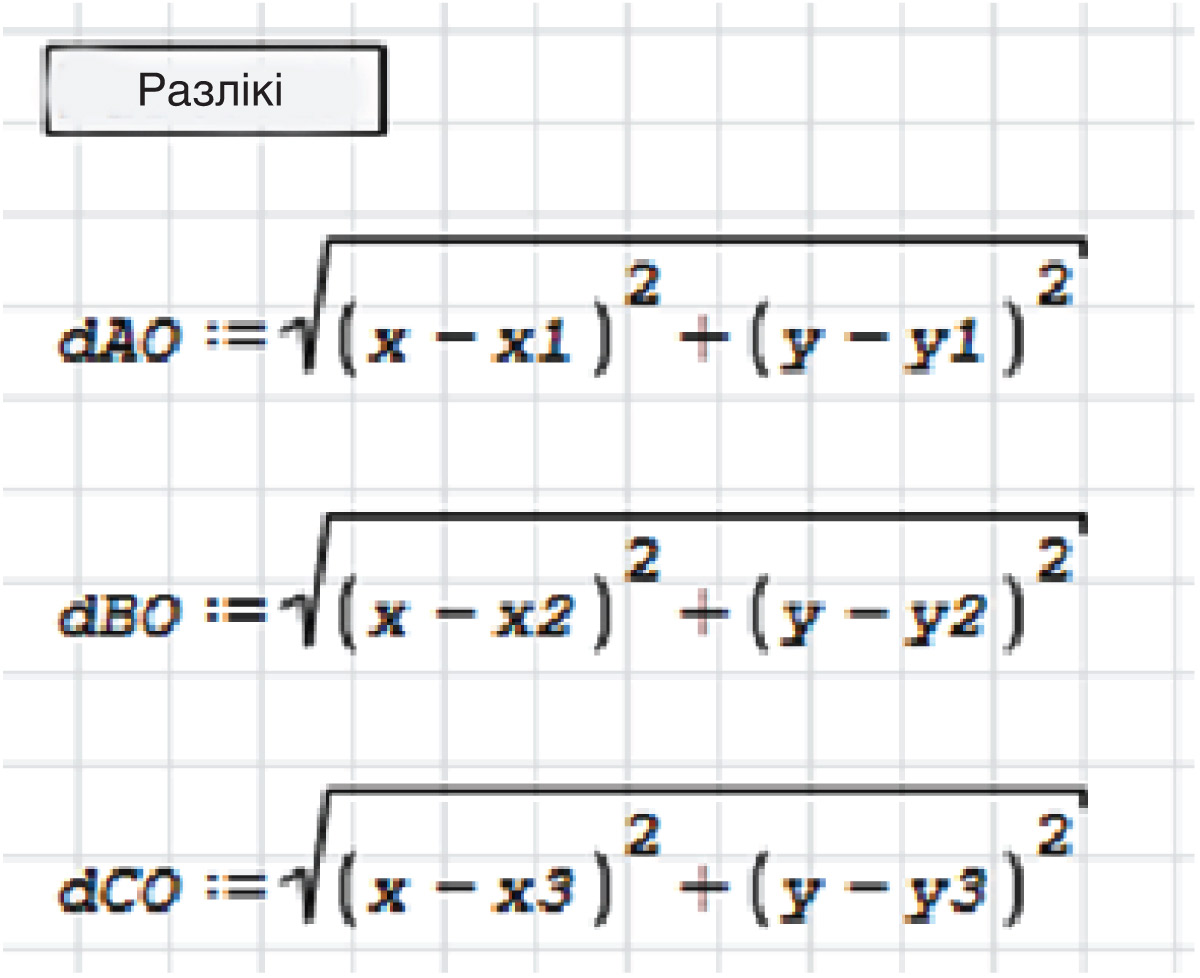§ 30. Мадэляванне ў задачах вылічэння каардынат выдатных пунктаў трохвугольніка
| Сайт: | Профильное обучение |
| Курс: | Інфарматыка. 11 клас (Павышаны ўзровень) |
| Книга: | § 30. Мадэляванне ў задачах вылічэння каардынат выдатных пунктаў трохвугольніка |
| Напечатано:: | Гость |
| Дата: | Суббота, 16 Август 2025, 02:47 |
Оглавление
- 30.1. Выдатныя пункты трохвугольніка
- 30.2. Пастаноўка задачы 1 (этап 1)
- 30.3. Выбар плана стварэння мадэлі (этап 2)
- 30.4. Стварэнне дакументальнай матэматычнай мадэлі (этап 3а)
- 30.5. Стварэнне камп'ютарнай мадэлі (этап 3б)
- 30.6. Даследаванне мадэлі (этап 4)
- 30.7. Атрыманне рашэння задачы 1 (этап 5)
- 30.8. Пастаноўка задачы 2 (этап 1)
- 30.9. Выбар плана стварэння мадэлі (этап 2)
- 30.10. Стварэнне дакументальнай матэматычнай мадэлі (этап 3а)
- 30.11. Стварэнне камп'ютарнай мадэлі (этап 3б)
- 30.12. Даследаванне мадэлі і атрыманне рашэння задачы 2 (этапы 4—5)
- 30.13. Пастаноўка задачы 3 (этап 1)
- 30.14. Выбар плана стварэння мадэлі (этап 2)
- 30.15. Стварэнне дакументальнай матэматычнай мадэлі (этап 3а)
- 30.16. Стварэнне камп'ютарнай мадэлі (этап 3б)
- 30.17. Даследаванне мадэлі і атрыманне рашэння задачы 3 (этапы 4—5)
- Практыкаванні
30.1. Выдатныя пункты трохвугольніка
|
Выдатныя пункты трохвугольніка — пункты, становішча якіх адназначна вызначаецца трохвугольнікам і не залежыць ад таго, у якім парадку бяруцца бакі і вяршыні трохвугольніка. Выдатных пунктаў трохвугольніка вядома вельмі шмат (прыклад 30.1). Мы разгледзім толькі тры такія пункты:
|
Прыклад 30.1. За мяжой выдатныя пункты трохвугольніка называюцца цэнтрамі трохвугольніка. У Інтэрнэце існуе энцыклапедыя цэнтраў трохвугольніка (The Encyclopedia of Triangle Centers). На пачатак 2021 года яна ўключала каля 40 000 апісанняў такіх цэнтраў. Энцыклапедыю цэнтраў трохвугольнікаў у 1994 годзе стварыў і з тых часоў дапаўняе прафесар матэматыкі ўніверсітэта Эвансвіла Кларк Кімберлінг. |
30.2. Пастаноўка задачы 1 (этап 1)
| Задача 1. На каардынатнай плоскасці трохвугольнік зададзены каардынатамі сваіх вяршынь. У пакеце SMath Studio пабудаваць камп'ютарную мадэль, якая дазваляе вылічыць каардынаты цэнтра апісанай акружнасці трохвугольніка, а таксама адлюстраваць трохвугольнік і апісаную акружнасць у графічнай вобласці (прыклад 30.2). |
Прыклад 30.2. Будзем весці пабудовы і разлікі для трохвугольнікаў, вяршыні якіх размешчаны ў першай чвэрці каардынатнай плоскасці. Для пабудоў возьмем трохвугольнік з вяршынямі: A(3;7), B(10;18), C(20;9). Мадэль назавем «Вылічэнне каардынат цэнтра апісанай акружнасці трохвугольніка». |
30.3. Выбар плана стварэння мадэлі (этап 2)
|
Паколькі праграмны сродак для вырашэння задачы зададзены, то пабудаваць, перш за ўсё, варта матэматычную мадэль (прыклад 30.3). Таму мадэль рашэння задачы створым па наступным простым плане: 3а — стварэнне дакументальнай матэматычнай мадэлі; 3б — стварэнне камп'ютарнай мадэлі ў пакеце SMath Studio. |
Прыклад 30.3. Формулы для разліку радыуса акружнасці, апісанай каля трохвугольніка, даўно і добра вядомыя. Для разліку каардынат цэнтра апісанай акружнасці можна выкарыстоўваць некалькі матэматычных метадаў, сярод якіх ёсць аналітычны з пабудовай ураўненняў перпендыкуляраў да сярэдзіны бакоў і метад увядзення невядомых каардынат цэнтра.
|
30.4. Стварэнне дакументальнай матэматычнай мадэлі (этап 3а)
|
Аналітычны метад дазваляе атрымаць рашэнне, але формулы прыйдзецца выводзіць без дапамогі пакета SMath Studio (прыклад 30.4). Метад увядзення невядомых дазваляе лічыць двума невядомымі каардынаты цэнтра апісанай акружнасці. Тады тры роўныя адлегласці ад цэнтра да вяршынь трохвугольніка дазволяць пабудаваць сістэму ўраўненняў і знайсці значэнні невядомых як рашэнні сістэмы. Выбіраем метад увядзення невядомых. Увядзем каардынаты вяршынь трохвугольніка як пераменныя: A(x1; y1), B(x2; y2), C(x3; y3). Цэнтр апісанай акружнасці пазначым O (лацінскае) з невядомымі каардынатамі x і y (прыклад 30.5). Абазначым dAO адлегласць паміж вяршыняй A і цэнтрам O. Тады Аналагічна вылічаюцца адлегласці dBO і dCO. Прыраўноўваем пары адлегласцей і атрымліваем сістэму двух ураўненняў адносна двух невядомых x і y |
Прыклад 30.4. Выкарыстанне аналітычнага метаду запатрабуе стварэння цэлага набору формул, уключаючы ўраўненні бакоў трохвугольніка і ўраўненні сярэдзінных перпендыкуляраў. Пры гэтым магчымасці пакета SMath Studio рэальна будуць выкарыстаны толькі для вылічэнняў па атрыманых формулах (у якасці калькулятара) і для пабудовы малюнкаў трохвугольніка і апісанай акружнасці ў графічнай вобласці пакета. Прыклад 30.5. Пераменныя для каардынат вяршынь трохвугольніка ўведзены для таго, каб мець магчымасць выкарыстоўваць пабудаваную мадэль для іншых зыходных даных. Значэнні гэтых пераменных каардынат, якія мы будзем выкарыстоўваць у разліках, зададзены намі ў прыкладзе 30.2. Увядзенне невядомых каардынат x і y для цэнтра апісанай акружнасці дазваляе выкарыстоўваць формулы для вылічэння адлегласцей паміж пунктамі на каардынатнай плоскасці і пабудаваць сістэму складаных ураўненняў, каб перадаць рашэнне гэтай сістэмы пакету SMath Studio. |
30.5. Стварэнне камп'ютарнай мадэлі (этап 3б)
|
Зыходныя даныя і пачатак разліковай табліцы размесцім па схеме, прыведзенай у прыкладзе 30.6. На працоўным лісце заўсёды ёсць магчымасць падраўнаваць верхнія межы некалькіх абласцей або іх левыя межы (прыклад 30.7). Тут жа ў зыходных даных ледзь ніжэй выведзем у графічнай вобласці малюнак трохвугольніка. Для гэтага падрыхтуем матрыцу каардынат вяршынь трохвугольніка і матрыцу параметраў тэксту.
Выводзім графічную вобласць, а ў ёй выводзім вектары V і P (гл. п. 29.4). Мяняем маштаб малюнка і становішча восей так, каб у вобласці быў бачны ўвесь трохвугольнік. Каб падняць літару B у графічнай вобласці, у другім радку матрыцы P замест y2 запішам y2 +2. Ніжэй уводзім загаловак «Разлікі» і формулы вылічэння адлегласцей ад вяршынь да цэнтра O апісанай акружнасці. Пры ўводзе падобных формул трэба максімальна выкарыстоўваць магчымасці капіравання і рэдагавання (прыклад 30.8). Складаем вектар сістэмы S, вектар невядомых Z і вектар Zo пачатковага набліжэння (гл. п. 28.2), які выбіраецца як ацэнка каардынат цэнтра апісанай акружнасці. Уводзім на працоўны ліст вектар пераменных і прысвойваем яму значэнне функцыі roots(), г. зн. лікавыя значэнні каардынат цэнтра акружнасці. Вектар пераменных захоўвае рашэнне сістэмы як значэнні пераменных x і y. Цяпер у графічнай вобласці трэба пабудаваць акружнасць і яе цэнтр (прыклад 30.9). |
Прыклад 30.6. Схема размяшчэння даных і загалоўкаў мадэлі. Прыклад 30.7. Каб выраўнаваць верхнія межы некалькіх абласцей, іх вылучаюць і пстрыкаюць па кнопцы Прыклад 30.8. Загаловак і формулы вылічэння адлегласцей ад вяршынь да цэнтра O. Першую формулу можна вылучыць, скапіраваць у буфер абмену і копію ўставіць ніжэй першай формулы. У другой формуле застаецца выправіць адну літару і два нумары каардынат. Аналагічна капіраваннем уводзіцца і трэцяя формула. Прыклад 30.9. Атрыманыя значэнні каардынат захаваны як значэнні пераменных x і y, і выкарыстоўваць іх у графічнай вобласці, якая размешчана на працоўным лісце вышэй, немагчыма. Таму пабудуем новую графічную вобласць ніжэй. Для гэтага вылучаем вектар P і графічную вобласць з трохвугольнікам з зыходных даных, капіруем іх у буфер абмену і ўстаўляем копіі на ліст ніжэй матэматычнай вобласці, у якой атрымана рашэнне сістэмы ўраўненняў. Пстрыкаем па правым ніжнім вуглу матрыцы-копіі параметраў тэксту P, націскаем клавішу Пробел (з'яўляецца вуглавая метка) і дапаўняем матрыцу P двума радкамі. |
30.6. Даследаванне мадэлі (этап 4)
|
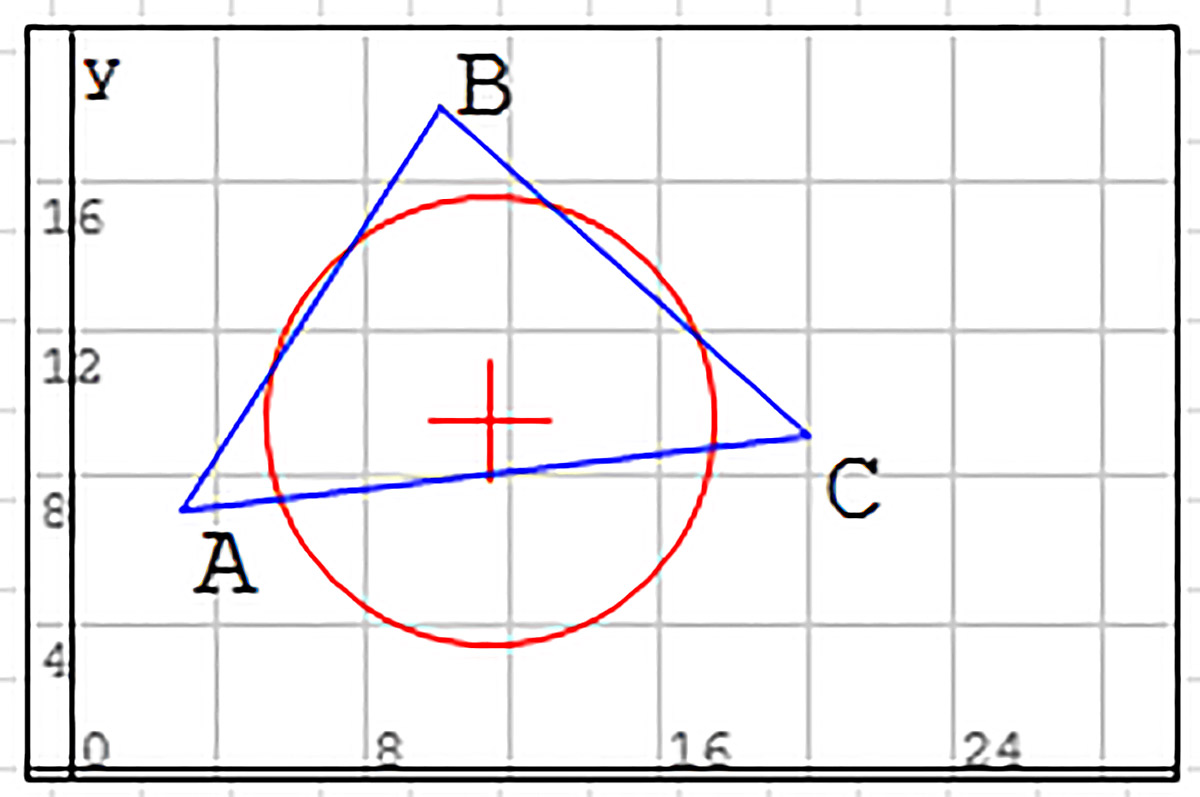
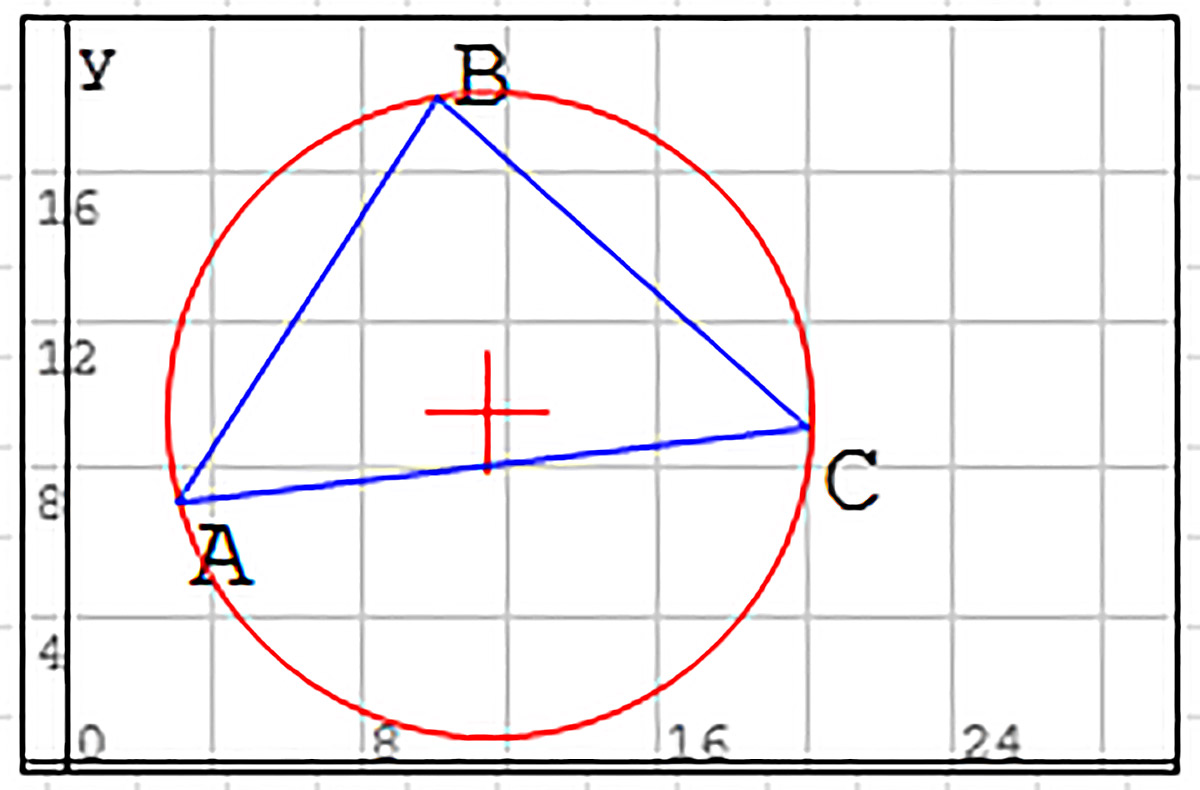
Калі памер акружнасці, якая называецца апісанай, можна падабраць так, што яна сапраўды пройдзе праз вяршыні трохвугольніка, то гэта графічна пацвярджае адэкватнасць пабудаванай мадэлі (прыклад 30.10). Радыус R апісанай акружнасці ў мадэлі даюць роўныя значэнні dAO, dBO і dCO. Для параўнання гэты радыус можна вылічыць па формуле (прыклад 30.11). |
30.7. Атрыманне рашэння задачы 1 (этап 5)
|
Задача 1 складалася ў пабудове камп'ютарнай мадэлі і гэтая задача вырашана. Пры іншых зыходных даных варта ўлічваць асаблівасці мадэлі (прыклад 30.12). |
Прыклад 30.12. Значэнню пачатковага набліжэння Zo на каардынатнай плоскасці адпавядае пункт, і для іншых зыходных даных Zo магчыма прыйдзецца падбіраць.
|
30.8. Пастаноўка задачы 2 (этап 1)
| Задача 2. На каардынатнай плоскасці трохвугольнік зададзены каардынатамі сваіх вяршынь. У пакеце SMath Studio пабудаваць камп'ютарную мадэль, якая дазваляе вылічыць каардынаты пункту перасячэння медыян трохвугольніка, а таксама адлюстраваць трохвугольнік і гэты пункт перасячэння ў графічнай вобласці (прыклад 30.13). |
Прыклад 30.13. Будзем весці пабудовы і разлікі для трохвугольнікаў, вяршыні якіх размешчаны ў першай чвэрці каардынатнай плоскасці. Для пабудоў возьмем трохвугольнік з вяршынямі A(3;7), B(10;18), C(20;9). Мадэль назавем «Вылічэнне каардынат пункту перасячэння медыян трохвугольніка». |
30.9. Выбар плана стварэння мадэлі (этап 2)
|
Аснову рашэння задачы 2 таксама складае матэматычная мадэль (прыклад 30.14). Таму мадэль рашэння задачы створым па наступным плане: 3а — стварэнне дакументальнай матэматычнай мадэлі; 3б — стварэнне камп'ютарнай мадэлі ў пакеце SMath Studio. |
Прыклад 30.14. Задача 2 гэтак жа, як і задача 1, мае аналітычнае рашэнне, але ў пакеце SMath Studio добра сябе паказаў метад увядзення невядомых. Сярод уласцівасцей пункта перасячэння медыян трохвугольніка ёсць уласцівасці, якія дазволяць пабудаваць мадэль у пакеце SMath Studio з выкарыстаннем метаду ўвядзення невядомых. |
30.10. Стварэнне дакументальнай матэматычнай мадэлі (этап 3а)
|
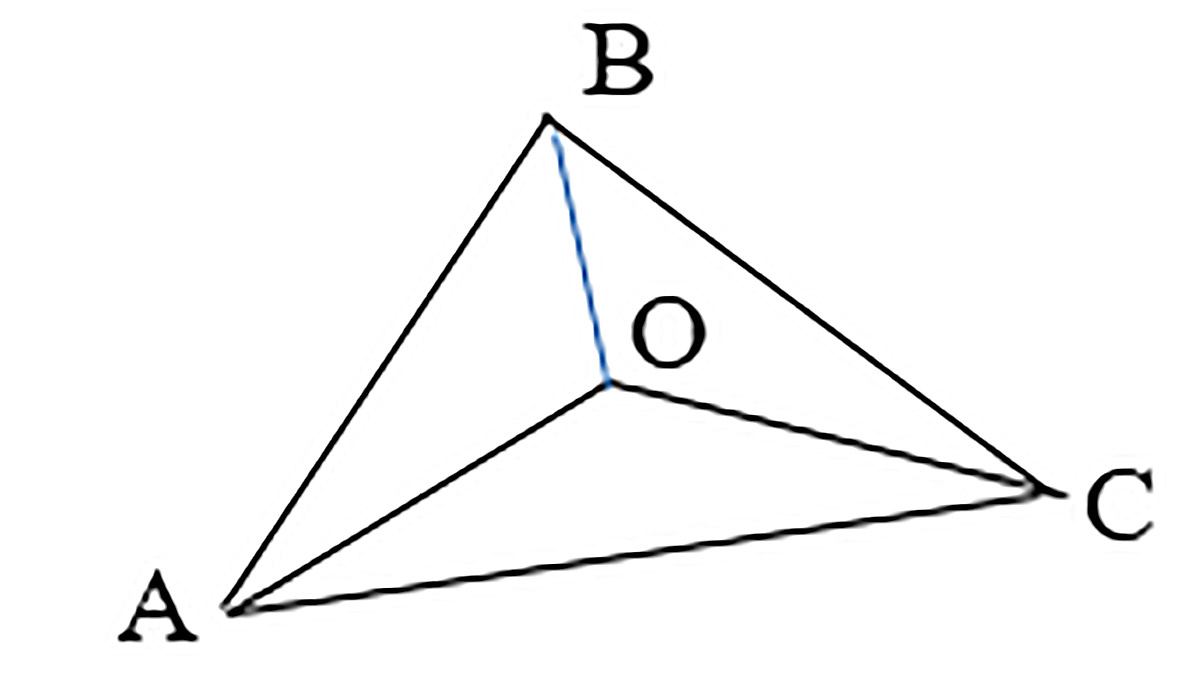
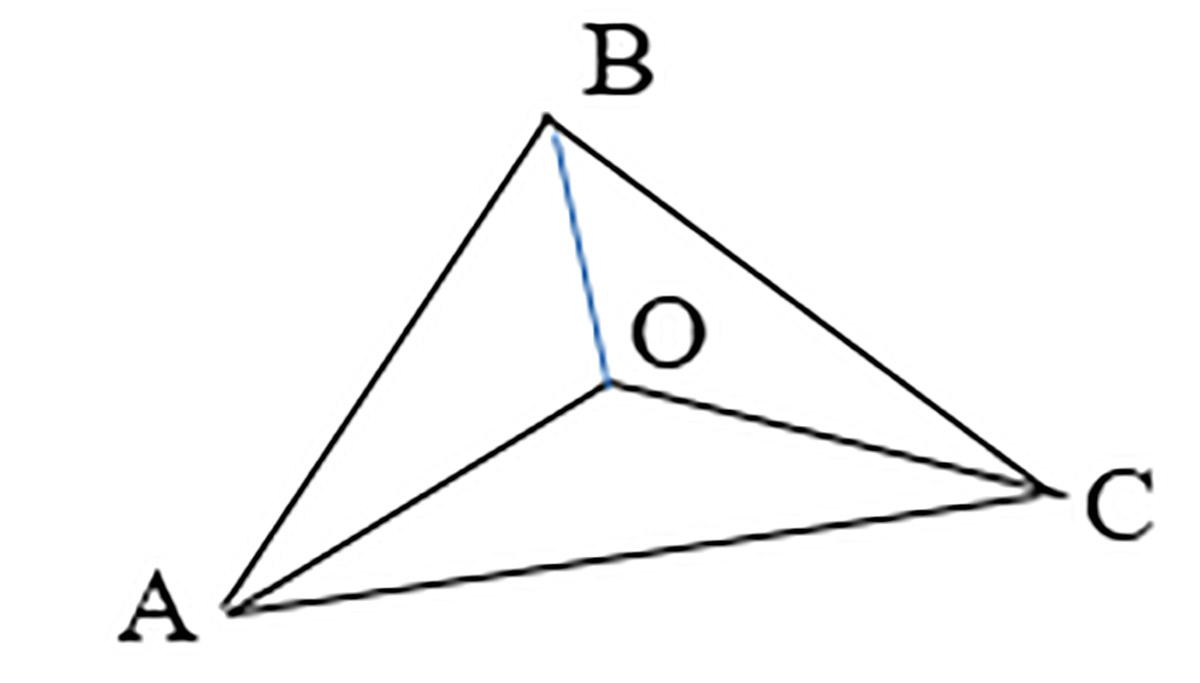
Захаваем абазначэнні задачы 1 для каардынат вяршынь: A(x1; y1), B(x2; y2), C(x3 ;y3), а абазначэнне О (лацінскае) з невядомымі каардынатамі x і y выкарыстоўваем для пункта перасячэння медыян трохвугольніка. Калі злучыць пункт O з вяршынямі трохвугольніка, то атрымаем тры трохвугольнікі (прыклад 30.15), плошчы якіх роўныя. Гэта ўласцівасць паслужыць асновай для стварэння сістэмы ўраўненняў. Для знаходжання плошчы трохвугольніка на каардынатнай плоскасці ёсць формула (прыклад 30.16). Прыраўноўваем пары плошчаў трохвугольнікаў і атрымліваем сістэму двух ураўненняў адносна двух невядомых, рашэнне якой з'яўляецца рашэннем задачы 2 (прыклад 30.17). |
Прыклад 30.15. Вынік пабудоў у трохвугольніку ABC. Прыклад 30.16. Формула разліку плошчы трохвугольніка AOB мае выгляд: sAOB = для трохвугольніка AOC: sAOC = для трохвугольніка BOC: sBOC = Прыклад 30.17. Сістэма ўраўненняў атрымае выгляд: |
30.11. Стварэнне камп'ютарнай мадэлі (этап 3б)
|
Скарыстаемся мадэллю задачы 1. Захоўваем яе ў файле пад іншым імем і будзем змяняць. Змяняем загаловак (гл. у прыкладзе 30.13), аднаўляем зыходныя даныя і выдаляем тры формулы разліку адлегласцей з раздзелу «Разлікі». На месца аддаленых формул уводзім формулы для разліку плошчаў трохвугольнікаў (прыклад 30.18). Зараз трэба змяніць вектар сістэмы S і прывесці яго да выгляду
Вектар Zo пачатковага набліжэння, як вектар меркаваных каардынат пункту перасячэння медыян, можна пакінуць са значэннямі 12; 10. Атрымліваем рашэнне
|
Прыклад 30.18. Першая формула мае выгляд: Пасля ўводу Астатнія формулы атрымліваюцца капіраваннем папярэдняй і рэдагаваннем. Прыклад 30.19. У ніжняй графічнай вобласці варта выдаліць малюнак акружнасці. Для гэтага пстрыкаем па правым ніжнім вуглу матрыцы параметраў тэксту P, націскаем клавішу Пробел. У шаблоне з'яўляецца ніжняя вуглавая метка. Перацягваючы метку паказальнікам мышы, выдаляем апошні радок матрыцы. У адказ малюнак акружнасці ў графічнай вобласці выдаляецца. |
30.12. Даследаванне мадэлі і атрыманне рашэння задачы 2 (этапы 4—5)
|
Праверку адэкватнасці мадэлі можна правесці аналітычнымі разлікамі (прыклад 30.20). Задача 2 складалася ў пабудове камп'ютарнай мадэлі і гэтая задача вырашана. |
Прыклад 30.20. Для правядзення аналітычных разлікаў ёсць некалькі метадаў, уключаючы вылічэнне каардынат сярэдзін бакоў трохвугольніка і пабудову ўраўненняў для медыян. Атрыманы каардынаты (11; 11
|
30.13. Пастаноўка задачы 3 (этап 1)
| Задача 3. На каардынатнай плоскасці трохвугольнік зададзены каардынатамі сваіх вяршынь. У пакеце SMath Studio пабудаваць камп'ютарную мадэль, якая дазваляе вылічыць каардынаты цэнтра упісанай акружнасці трохвугольніка, а таксама адлюстраваць трохвугольнік і ўпісаную акружнасць у графічнай вобласці (прыклад 30.21). |
Прыклад 30.21. Будзем весці пабудовы і разлікі для трохвугольнікаў, вяршыні якіх размешчаны ў першай чвэрці каардынатнай плоскасці. Для пабудоў возьмем трохвугольнік з вяршынямі: A(3;7), B(10;18), C(20;9). Мадэль назавем «Вылічэнне каардынат цэнтра ўпісанай акружнасці трохвугольніка». |
30.14. Выбар плана стварэння мадэлі (этап 2)
|
Аснову рашэння задачы 3 складае матэматычная мадэль (прыклад 30.22). Таму мадэль рашэння задачы створым па наступным плане: 3а — стварэнне дакументальнай матэматычнай мадэлі; 3б — стварэнне камп'ютарнай мадэлі ў пакеце SMath Studio. |
Прыклад 30.22. Задача 3 таксама мае аналітычнае рашэнне, але ў пакеце SMath Studio зручней выкарыстоўваць метад увядзення невядомых. Сярод уласцівасцей цэнтра ўпісанай акружнасці таксама ёсць уласцівасці, якія дазволяць пабудаваць мадэль у пакеце SMath Studio з выкарыстаннем метаду ўвядзення невядомых. |
30.15. Стварэнне дакументальнай матэматычнай мадэлі (этап 3а)
|
Захаваем абазначэнні задачы 1 для каардынат вяршынь: A(x1; y1), B(x2; y2), C(x3; y3), а абазначэнне O (лацінскае) з невядомымі каардынатамі x і y будзем выкарыстоўваць для цэнтра ўпісанай акружнасці. Адлегласць ад цэнтра ўпісанай акружнасці да аднаго боку трохвугольніка роўна адлегласці ад цэнтра да іншага боку і роўна радыуса ўпісанай акружнасці. Гэта ўласцівасць паслужыць асновай для стварэння сістэмы ўраўненняў. Для знаходжання адлегласці ад пункту да адрэзка на каардынатнай плоскасці ёсць формула (прыклад 30.23). Паколькі ўсе тры вышыні роўныя паміж сабой для цэнтра ўпісанай акружнасці, прыраўноўваем пары вышынь і атрымліваем сістэму двух ураўненняў адносна двух невядомых, рашэнне якой з'яўляецца рашэннем задачы 3.
|
Прыклад 30.23. Злучым адрэзкамі O і вяршыні трохвугольніка. Адлегласць ад пункта O да боку AB — гэта даўжыня вышыні ў трохвугольніку AOB, якую пазначым hAOB. Для вылічэння даўжыні вышыні праз плошчу sAOB трохвугольніка AOB ёсць формула
дзе dAB — даўжыня боку AB. Формулы для вылічэння плошчаў трохвугольнікаў і даўжынь бакоў мы ўжо ўводзілі. , Для вылічэння даўжынь вышынь двух іншых трохвугольнікаў аналагічна маем формулы
|
30.16. Стварэнне камп'ютарнай мадэлі (этап 3б)
|
Скарыстаемся мадэллю задачы 1. Захоўваем яе ў файле пад іншым імем і будзем змяняць. Змяняем адну літару ў загалоўку (гл. у прыкладзе 30.21), аднаўляем зыходныя даныя. Змяняем першыя тры формулы (прыклад 30.24). Загружаем файл з мадэллю задачы 2. Адкрываем яго, вылучаем першыя тры формулы раздзела «Разлікі», капіруем у буфер абмену, адкрываем ліст задачы 3 і ўстаўляем формулы на ліст правей першых трох. Затым пад першымі трыма формуламі ўстанаўліваем паказальнік месца ўводу і, націскаючы клавішу Enter, апускаем астатнія формулы на 9—10 клетак уніз, вызваляючы месца для формул вылічэння даўжынь вышынь (прыклад 30.25). Каб пакет выдаў рашэнне сістэмы і пабудаваў пункт цэнтра і акружнасць у графічнай вобласці, засталося памяняць вектар S сістэмы (прыклад 30.26). |
Прыклад 30.24. Формулу змяняем на Аналагічна другую і трэцюю формулы мяняем для вылічэння даўжынь бакоў dAC і dBC. Прыклад 30.25. Уводзім формулы для вылічэння даўжынь вышынь трохвугольнікаў з прыкладу 30.23. Прыклад 30.26. Вектар сістэмы задачы 1 мяняем на вектар сістэмы, атрыманай у п. 30.15. |
30.17. Даследаванне мадэлі і атрыманне рашэння задачы 3 (этапы 4—5)
|
Радыус r упісанай акружнасці ў мадэлі даюць роўныя значэнні hAOB, hAOC і hBOC. Для параўнання гэты радыус можна вылічыць па іншых формулах (прыклад 30.27). Задача 3 складалася ў пабудове камп'ютарнай мадэлі, і гэтая задача вырашана. |
Прыклад 30.27. Для радыуса ўпісанай акружнасці вядомая формула
дзе S — плошча трохвугольніка, а p яго паўперыметр. Па формуле атрымана r = 3,967. |
Практыкаванні

1. Паўтарыце на камп'ютары рашэнне задачы 1, разгледжанай у параграфе.
2. Знайдзіце рашэнне задачы 1 для трохвугольніка з каардынатамі вяршынь: A(2; 1), B(4; 14), C(17; 8).
3. Паўтарыце на камп'ютары рашэнне задачы 2, разгледжанай у параграфе.
4. Знайдзіце рашэнне задачы 2 для трохвугольніка з каардынатамі вяршынь: A(1; 3), B(15; –11), C(8; 15).
5. Паўтарыце на камп'ютары рашэнне задачы 3, разгледжанай у параграфе.
6. Знайдзіце рашэнне задачы 3 для трохвугольніка з каардынатамі вяршынь: A(1; –4), B(12; 14), C(16; –10).
7. Трохвугольнік зададзены каардынатамі сваіх вяршынь. Выкарыстоўваючы SMath Studio, знайсці каардынаты пункта перасячэння яго вышынь (артацэнтр) і пабудаваць чарцёж у графічнай вобласці.
Указанне. Калі вяршыні трохвугольніка пазначыць A, B і C, пункт перасячэння вышынь пазначыць O, а вышыні пазначыць AD, BE і CF , то пабудаваць сістэму ўраўненняў дазволіць вядомая роўнасць для даўжынь частак вышынь dAO·dOD = dBO·dOE = dCO·dOF.
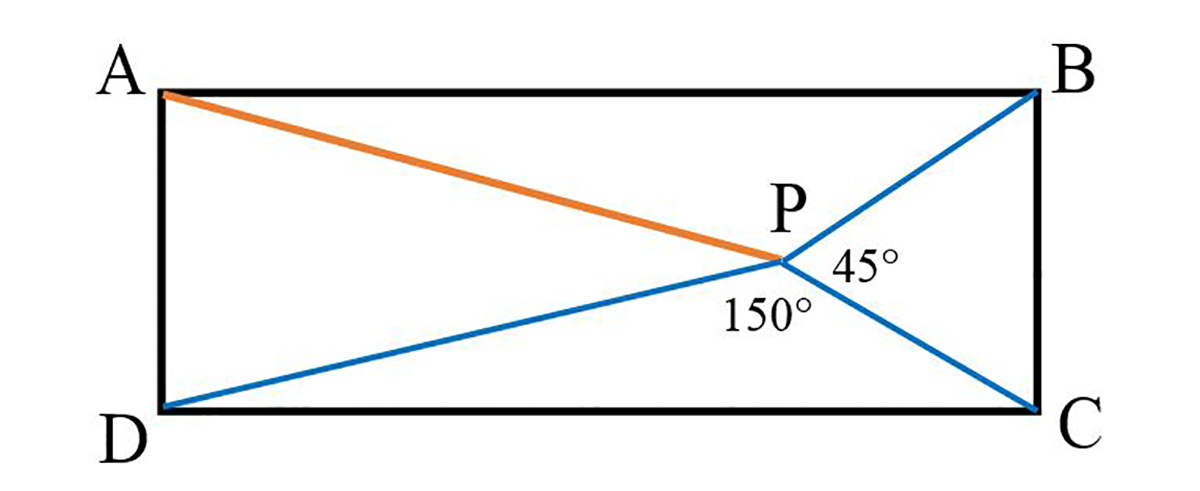
8. Дадзены прамавугольнік ABCD з бакамі 5 і 15. Унутраны пункт прамавугольніка P злучаны з вяршынямі прамавугольніка адрэзкамі прамых, пры гэтым вугал паміж адрэзкамі DP і CP роўны 150°, а вугал паміж адрэзкамі CP і BP роўны 45°. Выкарыстоўваючы SMath Studio, знайсці даўжыню адрэзка AP і адлюстраваць трохвугольнік з артацэнтрам у графічнай вобласці.
Указанне. Пабудаваць прамавугольнік на каардынатнай плоскасці, каб яго вяршыні атрымалі каардынаты. Праз невядомыя каардынаты пункта P выказаць вуглавыя каэфіцыенты прамых, на якіх ляжаць адрэзкі DP, CP і BP. Вуглавыя каэфіцыенты прамых з'яўляюцца тангенсамі нейкіх вуглоў. Рознасць адной пары вуглоў роўна 150°, а другой пары — 45°. Для вылічэння тангенса рознасці вуглоў ёсць формула. Дзве формулы дадуць два ўраўненні для вуглавых каэфіцыентаў. Гэтыя ўраўненні і ўтвараюць сістэму. Для атрымання рашэння сістэмы ўраўненняў кампаненты вектара Zo трэба выбіраць як каардынаты меркаванага становішча пункту P. Вылічыць даўжыню адрэзка AP па каардынатах яго канцоў. Пабудаваць чарцёж.
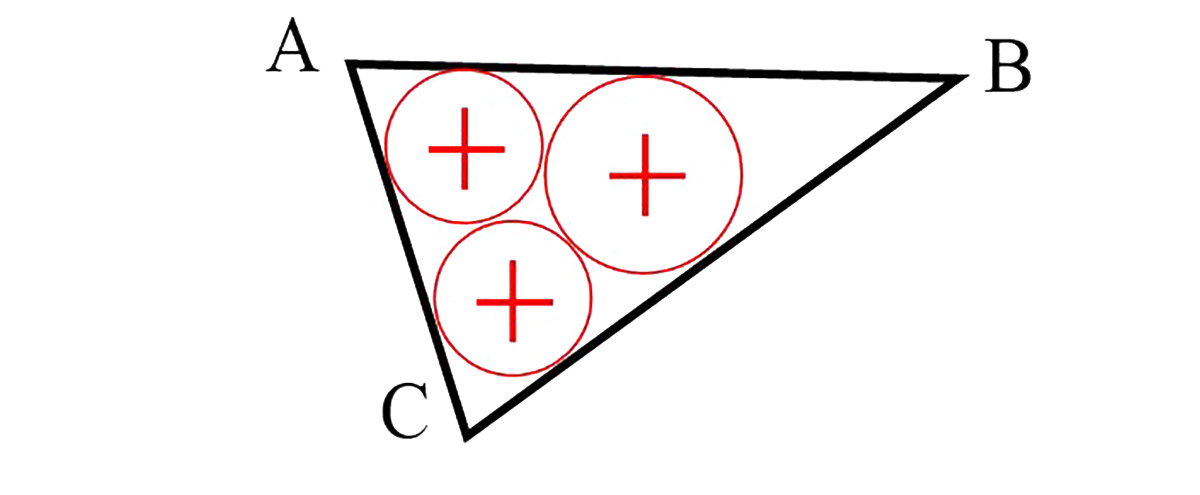
9*. Трохвугольнік зададзены каардынатамі сваіх вяршынь. Выкарыстоўваючы SMath Studio, знайсці каардынаты цэнтраў і радыусы трох акружнасцей, якія ўпісаны ў трохвугольнік і тычацца адзін аднаго, а таксама пабудаваць трохвугольнік і акружнасці у графічнай вобласці.