§ 10. Моделирование динамики численности популяций
| Сайт: | Профильное обучение |
| Курс: | Информационные технологии. 11 класс (Базовый уровень) |
| Книга: | § 10. Моделирование динамики численности популяций |
| Напечатано:: | Гость |
| Дата: | Воскресенье, 22 Декабрь 2024, 09:29 |
10.1. Основные понятия
|
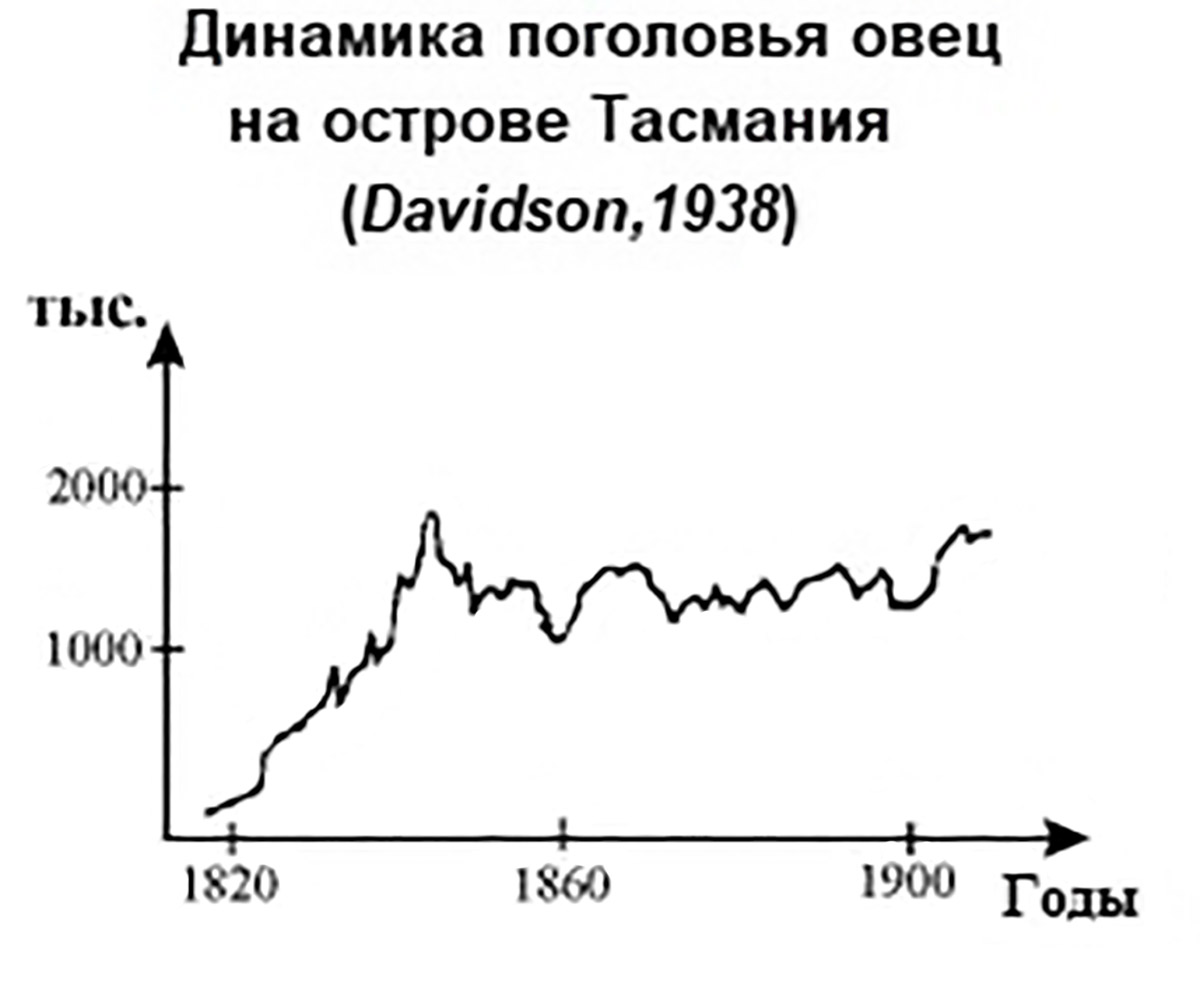
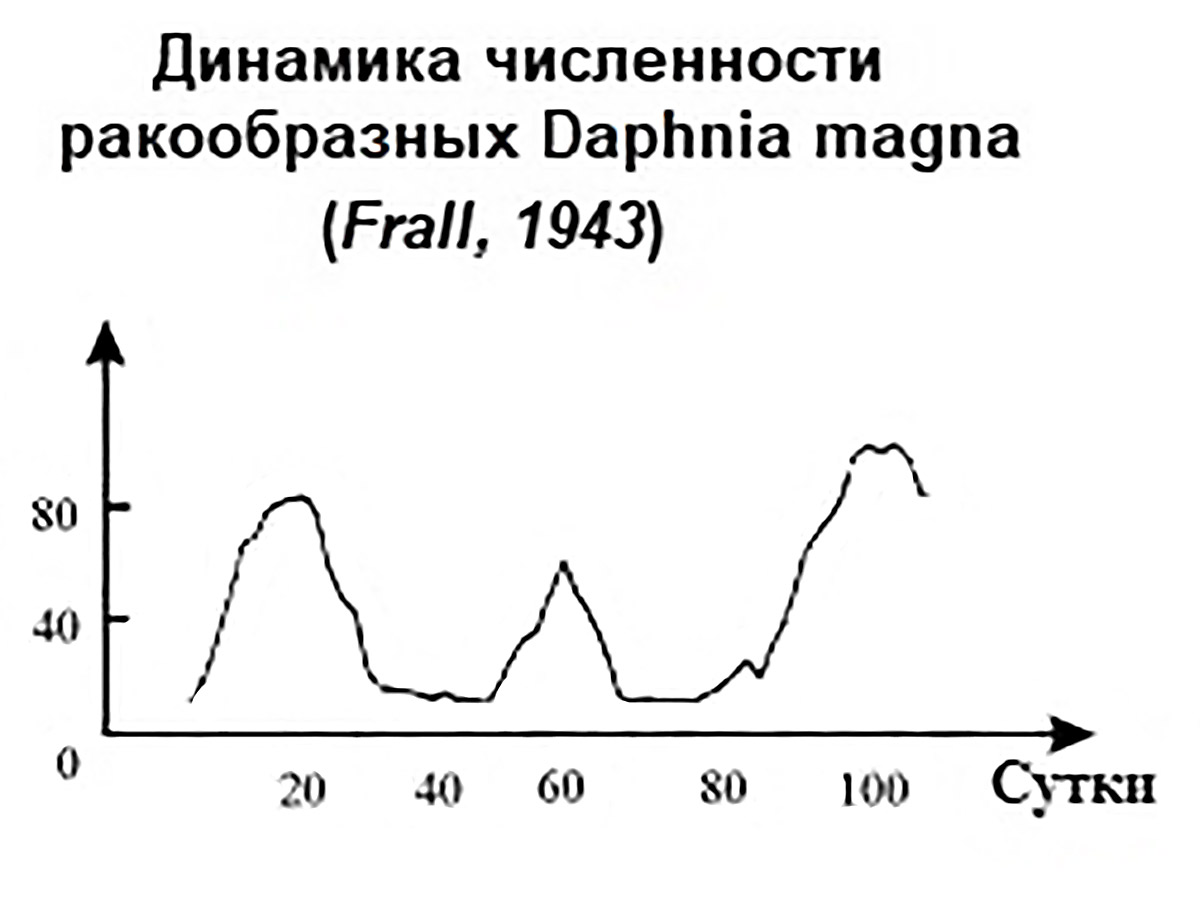
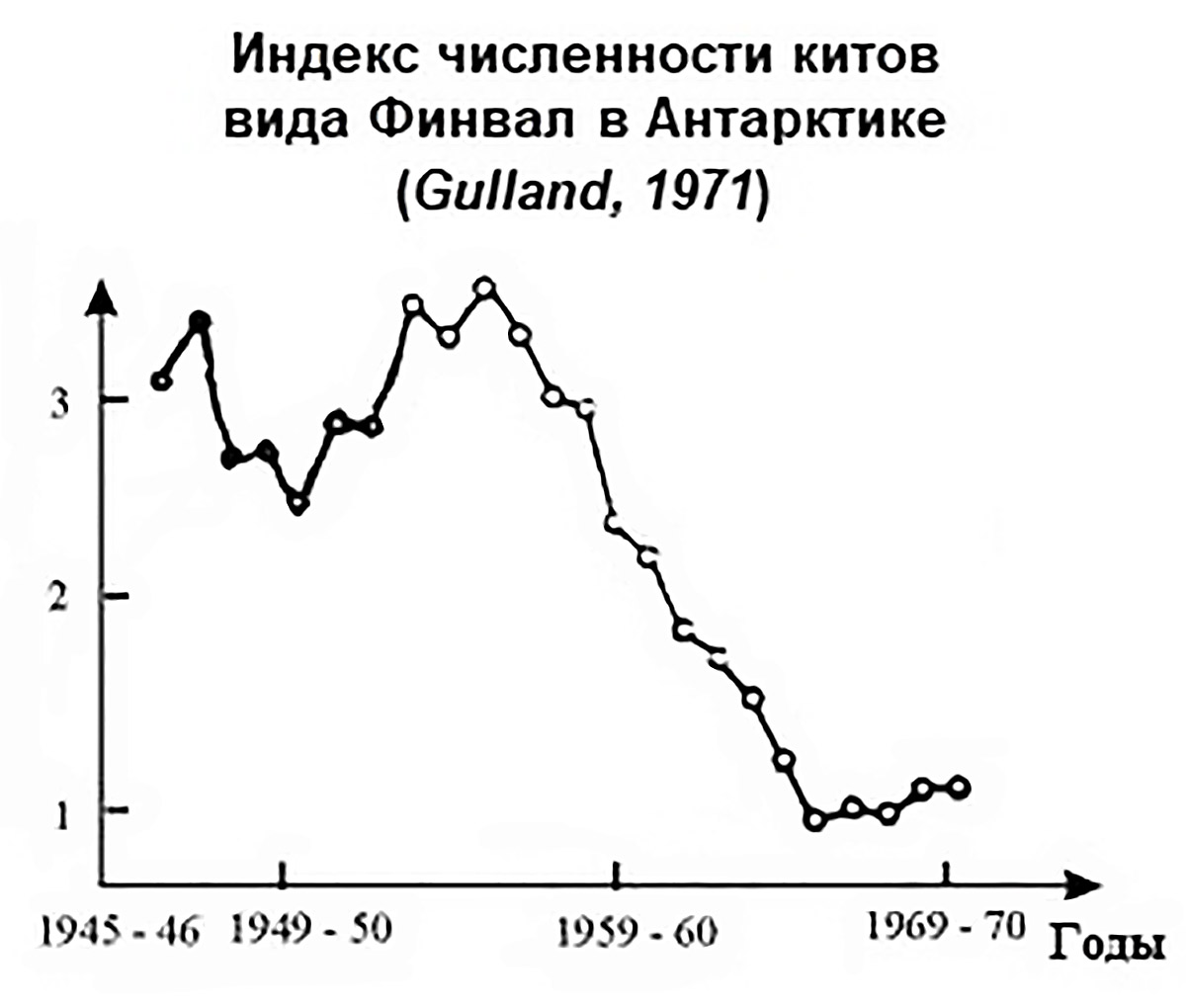
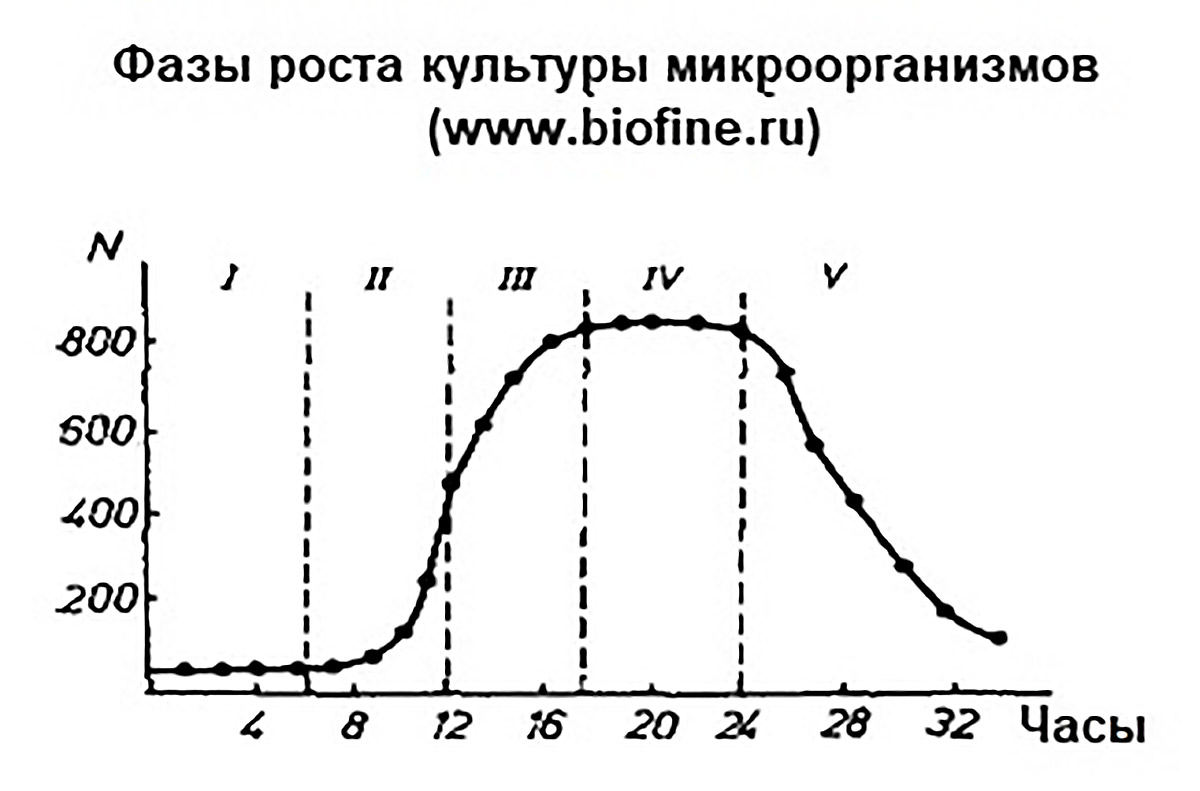
Популяция — это совокупность особей одного вида, которая занимает определенное пространство, относительно изолирована и способна к самовоспроизведению. Популяции образуют самые разнообразные организмы (пример 10.1). Среди характеристик популяции выделяют численность, плотность, пространственное распределение, структуру (возрастной и половой состав), показатели рождаемости и смертности. Нас будет интересовать динамика численности популяции, т.е. изменение численности популяции во времени (пример 10.2). Наблюдения за популяциями проводят в равноотстоящие моменты времени. Длительность промежутка времени между моментами наблюдений назовем периодичностью наблюдений. Периодичность наблюдений зависит от скорости роста популяции и может быть равна 1 году, 1 суткам, 1 часу (см. пример 10.2). Для описания динамики численности популяций ученые используют несколько математических моделей. Для одной популяции используются: - модель неограниченного роста; Для двух популяций используются модели взаимодействия двух видов. Среди них модель «хищник-жертва», модель конкуренции двух видов за ресурсы питания, модели взаимовыгодного взаимодействия (симбиоза). |
Пример 10.1. Популяции могут составлять бактерии, рыбы, ракообразные, киты, птицы, звери. Пример 10.2. Наблюдения за численностью различных популяций ученые ведут уже очень давно. Поэтому хорошо известно, что численность популяции во времени может расти, меняться циклически и падать.
|
10.2. Модель неограниченного роста
|
Модель неограниченного роста является классической математической моделью динамики численности популяции (пример 10.3). Если обозначить численность популяции в момент времени t через x(t), а скорость роста этой численности через v(t), то модель неограниченного роста выражается уравнением: v(t) = ax(t), где a — коэффициент естественного прироста. Коэффициент естественного прироста подсчитывается на основе наблюдений за численностью популяции (пример 10.4). Чтобы построить график решения уравнения, воспользуемся методом дискретизации времени с шагом x(ti +1) = x(ti ) + v(ti) а с учетом уравнения неограниченного роста получаем x(ti +1) = x(ti ) + ax(ti) Будем считать, что шаг времени x(i +1) = (1 + a) x(i). Расчеты по таким формулам удобно проводить в электронных таблицах. При i = 0 из формулы модели получаем основную формулу расчетной модели в электронных таблицах: x(1) = (1 + а)x(0). |
Пример 10.3. Модель была предложена английским священником и ученым Томасом Робертом Мальтусом в 1798 г.
Он первым обратил внимание на то, что рост численности популяции может сильно опережать рост ресурсов для ее питания. На этом основании для человеческой популяции он сделал вывод о неизбежности войн за ресурсы питания, наступления хаоса и голода. Пример 10.4. Коэффициент естественного прироста — это отношение численности прироста за период наблюдения к численности популяции на начало периода. Например, если численность популяции в 3000 особей за год выросла на 150 особей, то коэффициент естественного прироста равен
Интересно, что в модели популяция с коэффициентом прироста 0,05 удваивает свою численность через каждые 14 лет. Если в популяции рождаемость равна смертности, то коэффициент естественного прироста равен нулю и численность популяции остается без изменения. |
t. Пусть начальный момент t0 = 0, последующие моменты t1, t2, t3, … и скорость v(t) меняется только в эти моменты времени. Тогда значения x(ti +1) и x(ti ) связаны равенством
.10.3. Модель ограниченного роста
|
Наблюдения показали, что модель неограниченного роста справедлива только на ограниченных промежутках времени. Постоянный неограниченный рост популяции невозможен, прежде всего, из-за конкуренции внутри популяции за ресурсы питания. Осознание этого фактора привело к созданию математической модели ограниченного роста (пример 10.5). В обозначениях предыдущего пункта модель ограниченного роста выражается уравнением: v(t) = (a – bx(t))x(t), где a — коэффициент естественного прироста; b — коэффициент смертности от внутривидовой конкуренции (пример 10.6). Еще раз используем метод дискретизации времени с формулой x(ti +1) = x(ti ) + v(ti)∆t. Подставляем выражение для v(ti), считаем ∆t = 1, t0 = 0, ti = i и получаем x(i +1) = x(i) + (a – bx(i))x(i). Откуда при i = 0 получим расчетную формулу для электронных таблиц x(1) = x(0) + (a – bx(0))x(0). |
Пример 10.5. Модель ограниченного роста предложил в 1848 г. бельгийский математик Пьер Франсуа Ферхюльст.
Идея Ферхюльста состояла в том, что любая популяция, развиваясь, достигает своей максимальной численности, зависящей от факторов внешней среды. Пример 10.6. Коэффициенты a и b математической модели ограниченного роста определяют максимальную численность популяции как величину, равную дроби . А выражение a — bx(t) можно понимать как переменный коэффициент прироста. |
10.4. Модель с критической численностью
|
Существуют популяции, численность которых не может опускаться ниже некоторой критической численности. Иначе популяция погибает (пример 10.7). Математическая модель ограниченного роста, учитывающая наименьшую критическую численность, в обозначениях предыдущей модели имеет вид: v(t) = (a – bx(t))·(x(t) – L), где L — критическая численность популяции. С использованием метода дискретизации времени основная формула расчетной модели получает вид x(1) = x(0) + (a – bx(0))·(x(0) – L). |
Пример 10.7. Причина гибели популяции в том, что из-за ее малочисленности половозрелые особи популяции не находят друг друга в брачный сезон. Величина наименьшей критической численности различна для разных популяций. По наблюдениям биологов для ондатр критическая численность равна всего лишь одной паре особей на тысячу квадратных километров. А вот для американского странствующего голубя наименьшая критическая численность равна сотням тысяч особей. |
10.5. Модель с критической численностью и с отловом
|
Рассматриваемая модель описывает динамику численности популяции промысловой рыбы с критической численностью и с учетом ее промышленной добычи (пример 10.8). Оставляем в силе предположения предыдущих пунктов параграфа. Если объем регулярной добычи рыбы составляет Z особей популяции за время |
Пример 10.8. В океанах, морях, реках и озерах мира обитает более 30 тыс. видов рыб. Примерно 10% от этого числа составляют промысловые рыбы. Рыбой обеспечивается примерно одна шестая мировой потребности человечества в белке, что привело к сокращению ее запасов. Так, например, промысловые запасы трески, хека, морского окуня и камбалы в северной части Атлантики за последние годы сократились на 95 %. |
10.6. Создание компьютерной модели динамики численности популяций
|
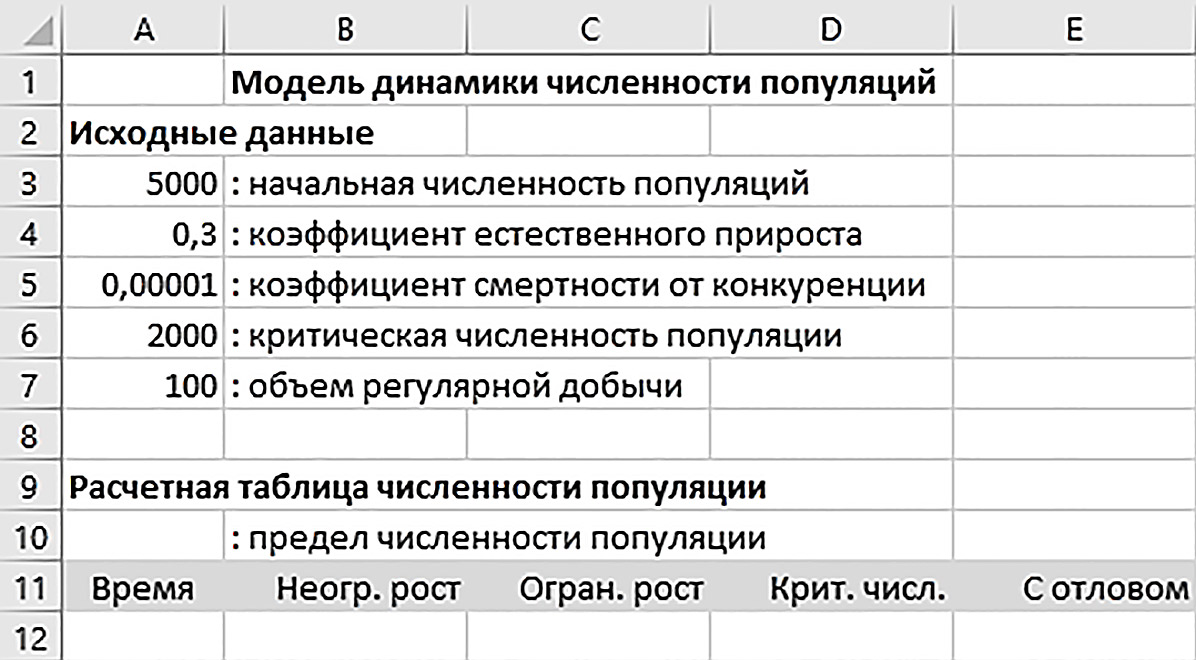
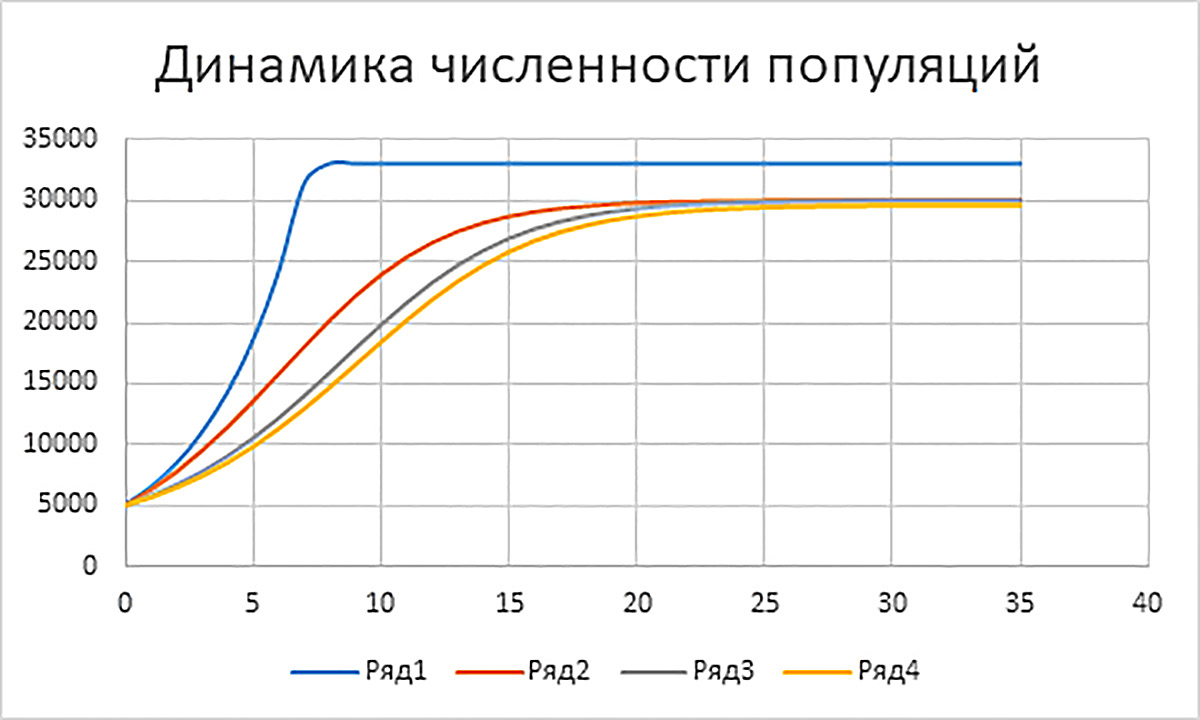
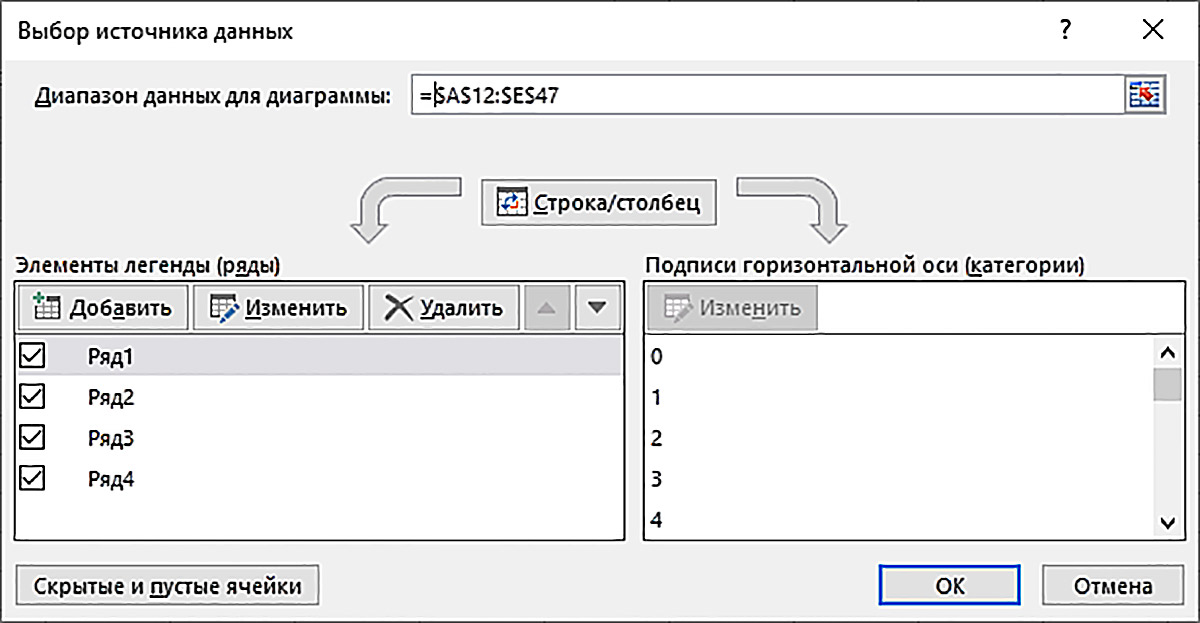
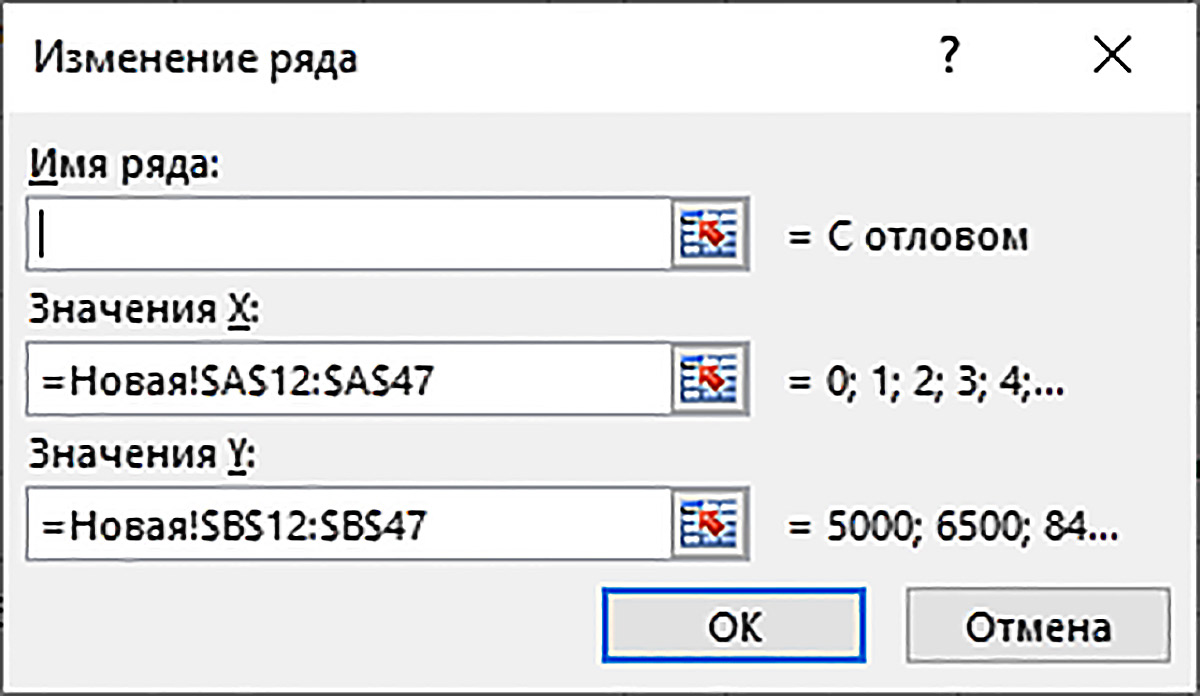
В электронных таблицах создадим комплексную компьютерную модель динамики численности четырех популяций, рассмотренных в п. 10.2—10.5 (пример 10.9). Для расчета численности популяции с неограниченным ростом используем формулу п. 10.2 x(1) = (1 + a)x(0). Для популяции с ограниченным ростом используем формулу п. 10.3 x(1) = x(0) + (a – bx(0))x(0). Для популяции с минимальной критической численностью используем формулу п. 10.4 x(1) = x(0) + (a – bx(0))·(x(0) – L). Для популяции с критической численностью и отловом используем формулу п. 10.5 x(1) = x(0) + (a – bx(0))·(x(0) – L) – Z. В исходных данных нужно задать значения параметров, записанных в правых частях этих формул (пример 10.9). Данные компьютерной расчетной модели разместим по схеме примера 10.10. Вводим формулы A10: =A4/A5 A12: 0 В ячейки B12:E12 вводим формулу =$A$3 В следующей строке A13: =A12+1 В ячейки B13:E13 нужно ввести правые части четырех расчетных формул. Значение x(0) для формулы в каждом столбце берется из предыдущей строки. B13: = (1 + $A$4)*B12 C13: = C12+($A$4-$A$5*C12)*C12 D13: =D12+($A$4—$A$5*D12)*(D12—$A$6) E13: =E12+($A$4—$A$5*E12)* (E12—$A$6)—$A$7 Формулы моделей требуют доработки (пример 10.11). Формулами диапазона A13:E13 таблица заполняется вниз до строки 47 включительно. Затем надо вывести на лист диаграмму с четырьмя графиками моделей. Выделяется диапазон A12:E47 в расчетной таблице и на лист рабочей книги вставляется диаграмма Точечная ( Осталось поменять имена элементов Диаграммы. Щелкаем по диаграмме правой клавишей мыши и в контекстном меню выбираем пункт Выбрать данные … . Появляется диалоговое окно Выбор источника данных (пример 10.13). В диалоговом окне слева выделяем строку Ряд1 и щелкаем по кнопке Изменить. Появляется диалоговое окно Изменение ряда (пример 10.14). В верхнее поле Имя ряда: щелчком по ячейке B11 вводим ссылку на заголовок второго столбца. Щелкаем кнопку OK. Имена остальных рядов изменяем аналогично.[1] Знак |
Пример 10.9. Исходные данные компьютерной модели должны включать: * численность x(0), начальную для всех четырех популяций; Пример 10.10. Комплексная компьютерная модель динамики численности популяций должна включать раздел Исходные данные и Расчетную таблицу. Используем следующую схему размещения данных:
Ширину столбцов B:E установим равной 13, для заголовков этих столбцов в расчетной таблице установим выравнивание вправо. Пример 10.11. Численность популяции в модели неограниченного роста растет очень быстро. Поэтому ограниченные численности остальных трех популяций на совместной диаграмме становятся практически незаметными. Чтобы избежать такого эффекта, искусственно ограничим численность в первой модели величиной ПЧ =1,1*$A$10, пользуясь тем, что в ячейке A10 вычислен предел численности популяции с ограниченным ростом. Для построения ограничения используем функцию ЕСЛИ() и в ячейку B13 вместо формулы модели неограниченного роста ФОРМН введем новую формулу по схеме =ЕСЛИ(ФОРМН<ПЧ; ФОРМН; ПЧ) Формулы остальных трех моделей в ячейках расчетной таблицы могут выдавать отрицательные значения численности популяций, что нарушает адекватность. Поэтому вместо формул ФОРМ этих моделей в ячейки С13:E13 введем новые формулы по схеме =ЕСЛИ(ФОРМ>0; ФОРМ; 0) Пример 10.12. Диаграмма с графиками компьютерной модели:
Пример 10.13. Диалоговое окно Выбор источника данных:
Пример 10.14. Диалоговое окно Изменение ряда:
|
— Точечная с гладкими кривыми). Вводится название диаграммы «Динамика численности популяций». В нижнюю часть диаграммы выводится Легенда 
10.7. Добавление интерактивных флажков
|
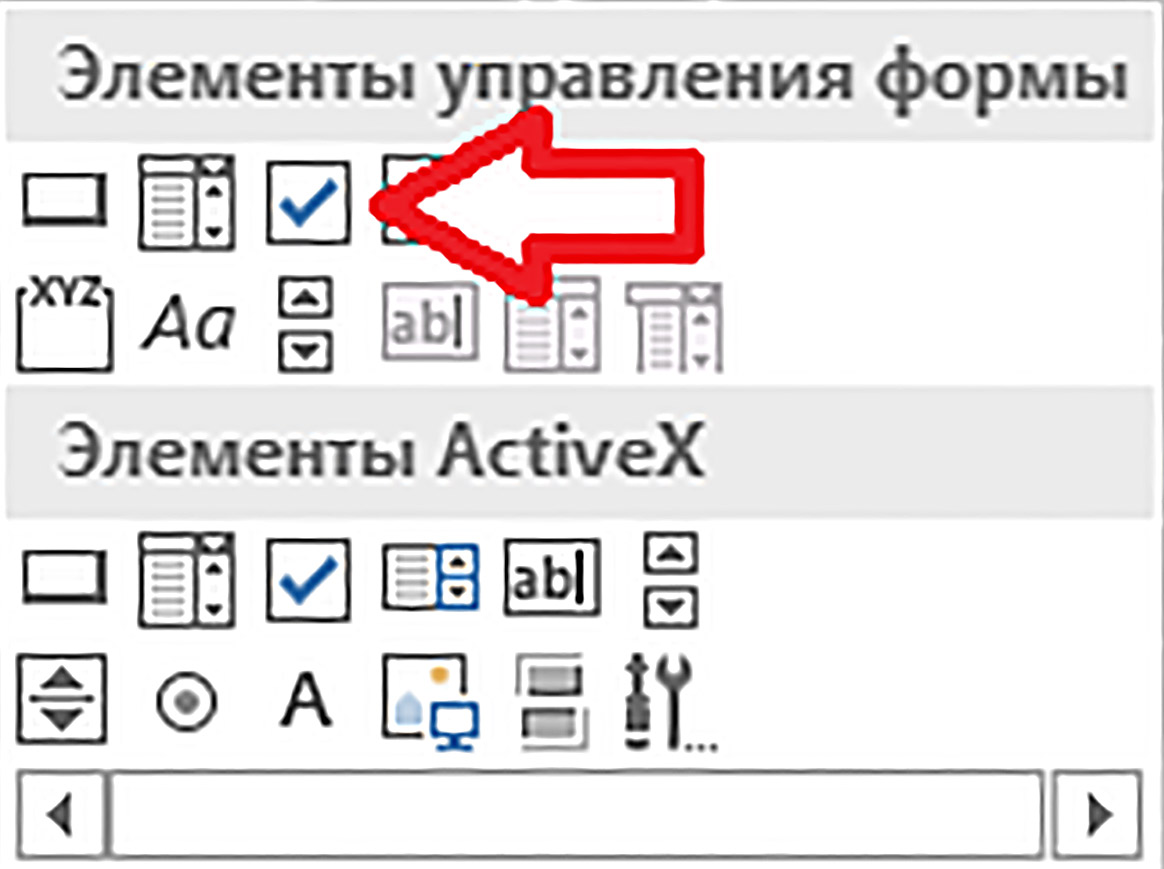
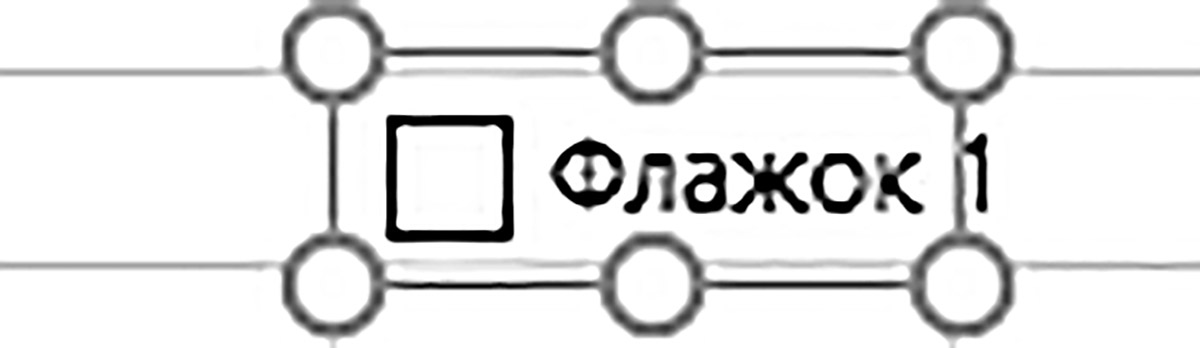
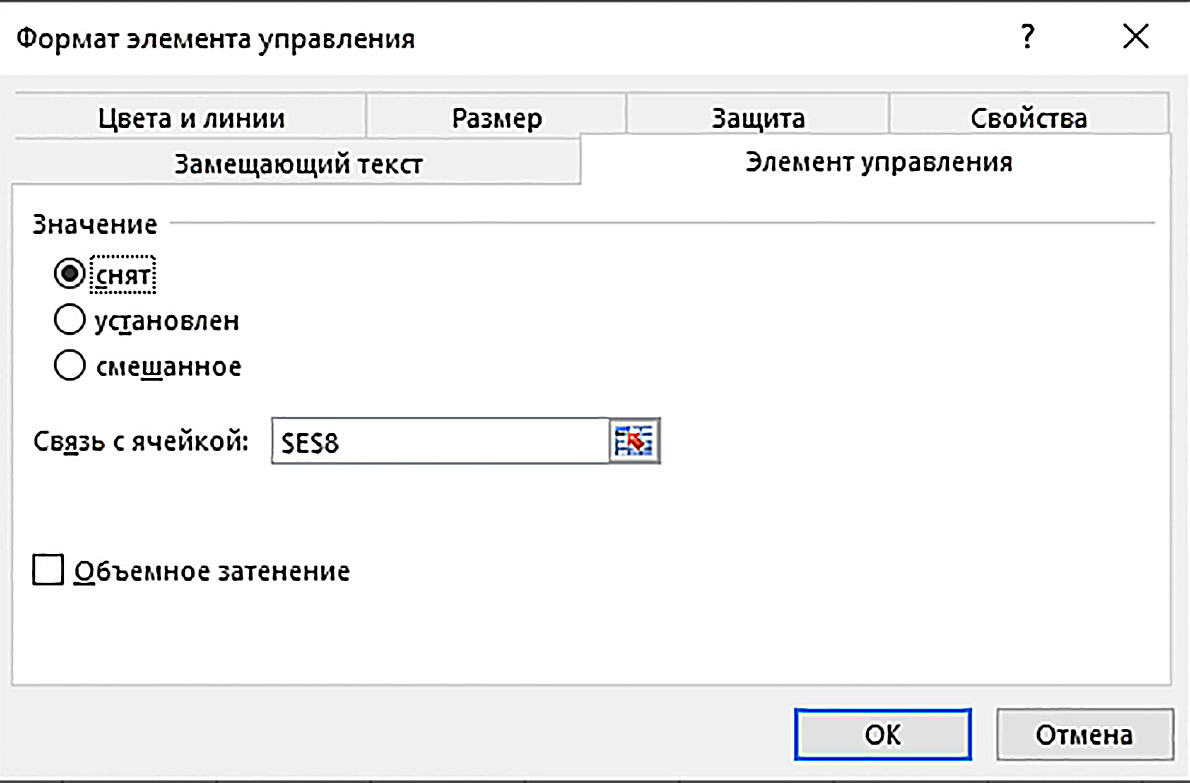
Работать сразу с четырьмя графиками на диаграмме не всегда удобно, поэтому добавим в компьютерную модель интерактивные флажки для выключения графиков на диаграмме. Работу с флажками обеспечивает вкладка Разработчик (пример 10.15). Для вывода флажка на лист на вкладке Разработчик в группе Элементы управления выбирают инструмент Вставить, а на его панели выбирают элемент управления формы Флажок (пример 10.16). После выбора щелчком элемента Флажок указатель мыши получает вид креста. Этим указателем мыши с нажатой левой кнопкой повторяют контур ячейки B8 вспомогательным прямоугольником (подобно рисованию прямоугольника в графическом редакторе Paint). После отпускания кнопки мыши на ячейке B8 появляется флажок в форме квадрата с названием по умолчанию. Флажок помещен в рамку с маркерами (пример 10.17). Название флажка по умолчанию надо удалить (пример 10.18). Флажок является графическим элементом, располагается поверх ячеек, и выделенный флажок можно перетаскивать по таблице. Флажок нужно аккуратно перетащить на ячейку B11 так, чтобы его квадрат размещался перед заголовком столбца (пример 10.19). В остальные ячейки с заголовками столбцов нужно вывести копии флажка (пример 10.20). Состояние флажка можно вывести в ячейку таблицы в виде значений ИСТИНА (флажок включен) и ЛОЖЬ (флажок выключен). Состояние первого флажка нужно вывести в ячейку B8 (пример 10.21). Щелчок по флажку теперь выводит галочку в квадрат и меняет значение связанной с флажком ячейки B8. Остальные флажки надо связать с ячейками C8:E8. Осталось изменить формулы в строке 12 таблицы. В ячейку B12 вводим формулу =ЕСЛИ(B8;$A$3;#Н/Д) Здесь #Н/Д — это искусственная ошибка, которая не позволит построить график. Формулой ячейки B12 заполняется вправо диапазон C12:E12. Теперь щелчки по флажкам выключают и включают графики на диаграмме. Значения состояний флажков в строке 8 можно сделать невидимыми, если в диапазоне B8:E8 установить белый цвет шрифта. |
Пример 10.15. Вкладка Разработчик выводится на экран командой: в Excel 2007 Офис → Параметры Excel → Отобразить вкладку Разработчик на ленте; в Excel 2010+ Файл → Параметры → Настройка ленты и в правом поле включить флаг у пункта Разрабочик. Настройка завершается кнопкой OK. Пример 10.16. Панель инструмента Вставить, на которой стрелкой указан верхний элемент Флажок для вставки.
Пример 10.17. Флажок с названием по умолчанию в рамке.
Рамка означает, что флажок выделен. При необходимости флажок выделяется щелчком правой клавишей мыши. Пример 10.18. По названию выделенного флажка щелкают, в рамке появляется текстовый курсор. Название флажка удаляют. Затем по флажку щелкают правой клавишей мыши и в новом меню выбирают пункт Завершить изменение текста. Пример 10.19. Флажок установлен на ячейку B11.
Пример 10.20. Нажимаем клавишу Ctrl клавиатуры и устанавливаем указатель мыши на рамку выделенного флажка так, чтобы указатель получил вид стрелки с плюсом Перетаскиваем и устанавливаем флажок-копию на другую ячейку. Аналогично устанавливаем остальные два флажка. Пример 10.21. Щелкаем по флажку правой клавишей мыши и в меню выбираем пункт Формат объекта … . Появляется диалоговое окно:
|
.
Упражнения
1. Повторите на компьютере рассмотренное в параграфе построение комплексной компьютерной модели динамики численности популяций. Введите в модель исходные данные, приведенные на схеме примера 10.10. Для ячеек расчетной таблицы следует задать формат Числовой с числом десятичных знаков 0 (целые числа).
Проверьте адекватность модели сравнением данных ее строки 47 со следующими выверенными данными
2. В модели динамики численности популяций с исходными данными примера 10.10 оставьте включенными графики моделей неограниченного и ограниченного роста. Увеличивая постепенно начальную численность популяций от 5000 до 25000 с шагом 5000, проанализируйте взаимное положение двух графиков.
3. В модели динамики численности популяций с исходными данными примера 10.10 оставьте включенными графики модели ограниченного роста и модели с критической численностью. Уменьшая постепенно начальную численность популяций от 3000 до 1600 с шагом 200, проанализируйте положение графиков и объясните их поведение.
4. В модели динамики численности популяций с исходными данными примера 10.10 оставьте включенными графики модели с критической численностью и модели с отловом. Постепенно увеличивая объем регулярной добычи от 100 до 1200 с шагом 100, опишите поведение графика модели с отловом. Найдите максимальное значение объема отлова, при котором популяция еще может восстановиться.