§ 20. Праходжанне святла праз аптычныя элементы

Законы адбіцця і праламлення святла шырока выкарыстоўваюцца для кіравання ходам светлавых пучкоў. Для адбіцця святла ў прыборах прымяняюцца люстры і прызмы, для праламлення — прызмы, плоскапаралельныя пласцінкі (мал. 137), лінзы. Люстры, прызмы, пласцінкі і лінзы з’яўляюцца элементамі, камбінуючы якія ствараюць розныя аптычныя прыборы. Як яны працуюць?

Плоскапаралельная пласцінка

Разгледзім ход светлавога праменя ад крыніцы ў плоскапаралельнай пласцінцы таўшчынёй d, якая знаходзіцца ў паветры (мал. 138, а). Згодна з законам праламлення, на першай і другой межах падзелу для праменя, які падае пад вуглом a на першую мяжу, маем (мал. 138, б):  

Тут γ — вугал праламлення на першай мяжы, α₁ — вугал падзення на другую мяжу, γ₁ — вугал праламлення на другой мяжы, n — абсалютны паказчык праламлення рэчыва пласцінкі.

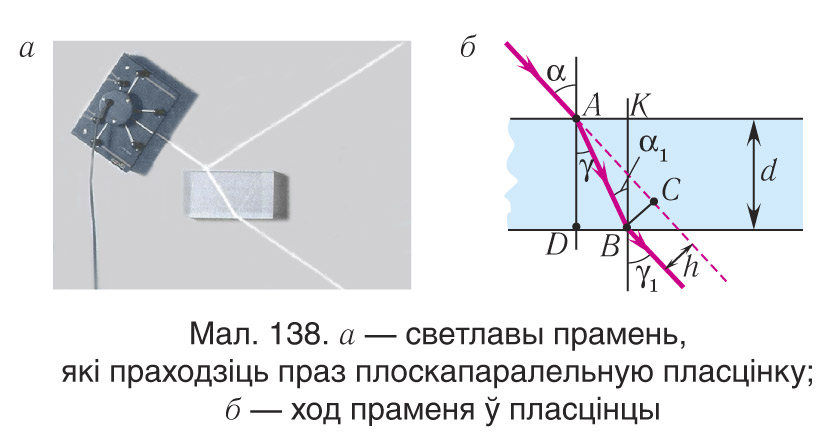Накрыж ляжачыя вуглы γ і α₁ пры паралельных прамых AD і BK (перпендыкулярах да першай і другой паралельных меж) роўныя, г. зн. α₁ = γ. Значыць, sinα = nsinγ = nsinα₁  = sinγ₁ Адкуль вынікае, што:

Такім чынам, прамень святла, праходзячы праз плоскапаралельную пласцінку, з абодвух бакоў якой знаходзіцца адно і тое ж асяроддзе, зрушваецца на некаторую адлегласць h = BC перпендыкулярна да свайго пачатковага напрамку (гл. мал. 138, б).

Адпаведна, усе прадметы, калі глядзець на іх скрозь празрыстую плоскапаралельную пласцінку пад вуглом, не роўным нулю, будуць таксама здавацца зрушанымі. 

Як бачна на малюнку 138, а, прамені, адбітыя ад верхняй і ніжняй граней пласцінкі, паралельны адзін аднаму на выхадзе з яе.

Знойдзем, ад якіх параметраў пласцінкі залежыць зрушэнне h праменя

З  вынікае, што:

З  маем:

.

Адкуль:

З улікам закона праламлення  і трыганаметрычнай тоеснасці  sin²γ + cos²γ  = 1 знаходзім:

Канчаткова, адлегласць h паміж напрамкамі ўваходнага і выходнага праменяў можна вызначыць з суадносіны:

.

(1-1)

Як бачна з суадносіны (1-1), зрушэнне h праменя пры дадзеным вугле падзення α залежыці ад таўшчыні d пласцінкі і яе паказчыка праламлення n.

Трохграневая прызма

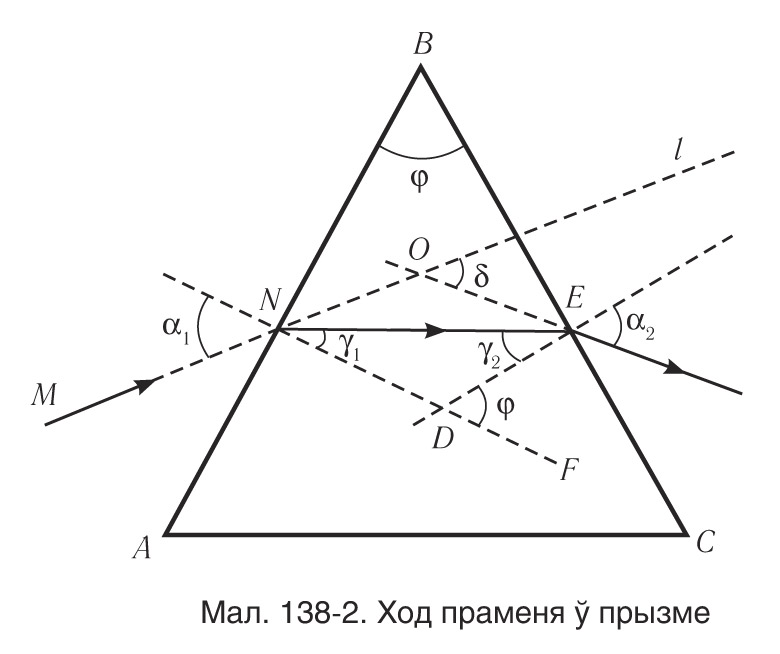
Разгледзім ход праменя ў трохграневай прызме. Няхай светлавы прамень NM падае пад вуглом α₁ на бакавую грань трохграневай прызмы ABC, сячэнне якой паказана на малюнку 138-2. Прызма, вырабленая з рэчыва з абсалютным паказчыкам праламлення n₂ , знаходзіцца ў асяроддзі з абсалютным паказчыкам праламлення n₁. Грані прызмы, праходзячы праз якія прамені святла праламляюцца, называюцца праламляльнымі. Грань, якая ляжыць насупраць праламляльнага вугла, называецца асновай прызмы. Вугал φ пры вяршыні B трохвугольніка  называецца праламляльным вуглом прызмы.

Няхай прамень  і   ляжаць у адной плоскасці — плоскасці аркуша кнігі. З закона праламлення святла знаходзім вугал праламлення γ₁:

.

(1-2)

Калі паказчык прызмы n₂ > n₁ , то праломлены прамень NE падае на другую бакавую грань прызмы пад вуглом γ₂. Поўнае адбіццё на другой праламляльнай грані не адбываецца пры ўмове  і прамень выходзіць з прызмы пад вуглом α₂. Яго знаходзім з закона праламлення:

.

(1-3)

Адхіленне ад пачатковага напрамку праменя  у выніку праламленняў на гранях прызмы вызначаецца LOE = δ   (гл. мал. 138-2). Вугал δ паміж напрамкамі ўваходнага і выходнага праменяў называецца вуглом адхілення. Разгледзім . У ім  па тэарэме аб знешнім вугле трозвугольніка знаходзім:

Выкарыстаем гэтую ж тэарэму да :

З формул (1-4) і (1-5) вызначым сувязь вугла падзення α₁, вугла праламлення α₂ з праламляльным вуглом прызмы φ і вуглом адхілення δ выходнага праменя пачатковага напрамку:

У выніку атрымалі сістэму ўраўненняў (1-2), (1-3), (1-4), (1-6):

(1-7)

Сістэма ўраўненняў (1—7) дазваляе рашыць задачу на праходжанне праменя святла праз трохграневую прызму без поўнага адбіцця на яе гранях.

Калі вугал падзення α₁ на грань прызмы і праламляльны вугал прызмы φ малыя, то малымі будуць і вуглы ,  γ₁, γ₂, α₂  Таму ў законах праламлення (1-2) і (1-3) адносіну сінусаў можна замяніць адносінай вуглоў, выражаных у радыянах, г. зн.

.

(1-8)

Падставіўшы выразы для (1-8) α₁ і  α₂  у суадносіну (7), знойдзем

.

(1-9)

З суадносіны (1-9) вынікае, што: па-першае, чым большы праламляльны вугал φ, тым большы вугал адхілення δ праменяў прызмай; па-другое, вугал адхілення δ праменяў павялічваецца з ростам абсалютнага паказчыка праламлення n₂ рэчыва прызмы. Як бачна з малюнка 138-2, прамень святла, праходзячы праз трохграневую прызму, адхіляецца да яе патоўшчанай частцы, калі абсалютны паказчык праламлення рэчыва прызмы большы за абсалютны паказчык праламлення навакольнага асяроддзя (n₁ > n₂).

На малюнку 139 паказана трохгранная прызма. Прамень святла, праходзячы праз трохгранную прызму, адхіляецца ад свайго пачатковага напрамку распаўсюджвання да асновы (патоўшчанай часткі) прызмы. Падкрэслім, што гэта справядліва ў тым выпадку, калі абсалютны паказчык праламлення рэчыва прызмы большы за абсалютны паказчык праламлення навакольнага асяроддзя  . Звярніце ўвагу, што калі на прызму падае прамень белага святла, то пасля праходжання прызмы на экране назіраецца рознакаляровая палоска, якая змяшчае набор колераў — ад чырвонага да фіялетавага. Ісак Ньютан, які ўпершыню правёў дадзены эксперымент, назваў гэту палоску спектрам. Парадак следавання колераў у спектры лёгка запомніць з дапамогай вядомай фразы:  чырвоны — 770—630 нм                     чыж аранжавы — 630—590 нм                   аддаў жоўты — 590—570 нм                         жуку зялёный — 570—495 нм                      загад: блакітны, сіні — 495—435 нм             брат, схавай фіялетавы — 435—390 нм                   фотаапарат

Пытаннi да параграфу

1. Намалюйце ход светлавога праменя ў плоскапаралельнай пласцінцы.
2. Пры якім вугле падзення прамень святла, праходзячы праз плоскапаралельную пласцінку, не зрушваецца
3. Намалюйце ход светлавога праменя ў трохграневай прызме.
4. Як паводзіць сябе светлавы пучок пры праходжанні праз шкляную прызму?
5. Пры якіх умовах прамень, што ідзе паралельна аснове раўнабедранай прызмы, пры падзенні на яе бакавую грань не зменіць свайго напрамку?
6. Ці застанецца паралельным пучок монахраматычнага святла, праходзячы праз трохграневую прызму, калі ён быў паралельным пры падзенні на праламляльную грань прызмы?

 

Прыклад рашэння задачы

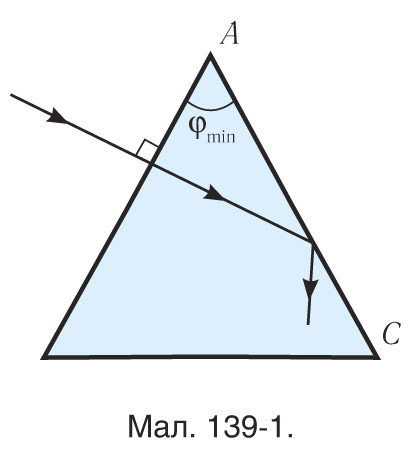
Вызначыце найменшы праламляльны вугал φ_min шкляной прызмы, што знаходзіцца ў паветры, пры якім прамень, падаючы нармальна на грань прызмы, не выйдзе праз яе другую бакавую грань (мал. 139-1). Паказчык праламлення шкла прызмы   n = 1,6.

Практыкаванне 16

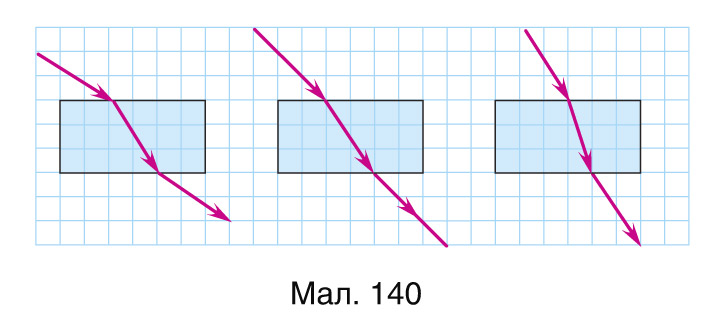
1. Вызначыце паказчык праламлення пласцінкі, зыходзячы з ходу праменяў на малюнку 140. Навакольнае асяроддзе — паветра (n = 1,0)

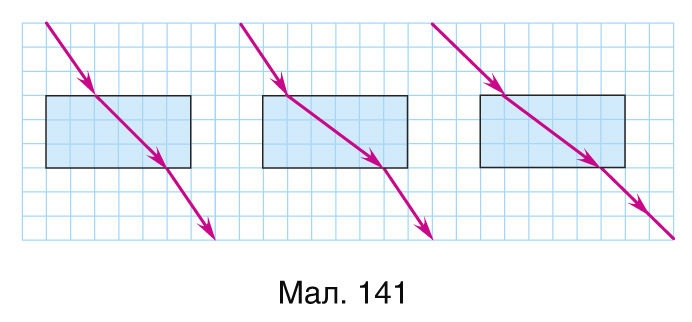
2. Вызначыце паказчык праламлення пласцінкі, зыходзячы з ходу праменяў на малюнку 141, калі паказчык праламлення навакольнага асяроддзя n = 2,0.

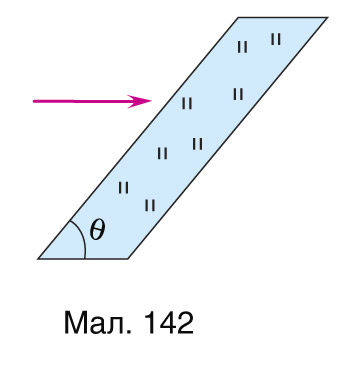
3. Пабудуйце ход праменя ў пласцінках са шкла з паказчыкам праламлення n = 1,5 (мал. 142, 143), калі вугал 

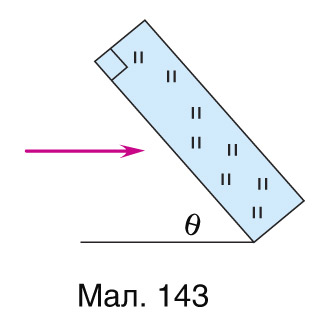4. Вызначыце зрушэнне h праменя святла пры яго падзенні пад вуглом α=45° на шкляную плоскапаралельную пласцінку таўшчынёй d =6,0 мм, калі паказчык праламлення шкла n =1,5 .
5. Вугал падзення двух паралельных праменяў святла на плоскапаралельную шкляную пласцінку (n=1,6) роўны α=30°, а адлегласць паміж імі l₀=20мм. Вызначыце адлегласць l паміж праменямі ў пласцінцы.
6. На плоскапаралельную плацінку (n=1,5), ніжняя паверхня якой пасярэбрана, падае прамень святла пад вуглом α=30°. Вызначыце таўшчыню d пласцінкі, калі ў выніку адбіцця ад ніжняй грані ўтвараюцца два адбітыя прамені, якія знаходзяцца на адлегласці  l=40мм  адзін ад аднаго.
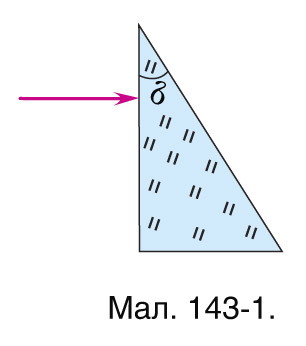
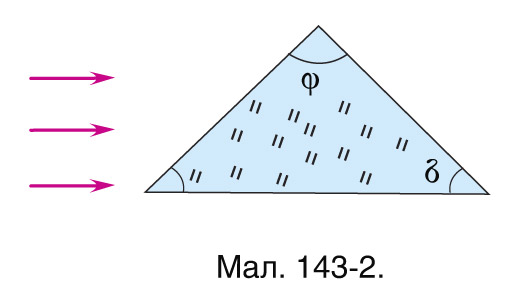
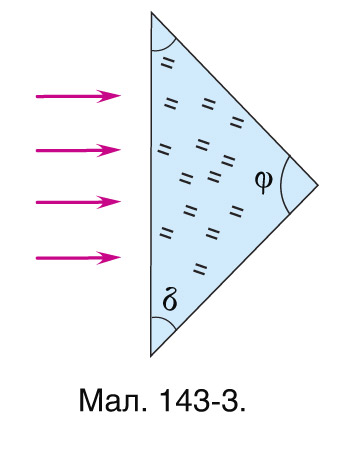
7. Пабудуйце ход праменя ў прызме са шкла з паказчыкам праламлення n=1,5 (мал. 143-1, 143-2, 143-3).
8. Вызначыце праламляльны вугал φ шкляной прызмы, калі прамень, які падае перпендыкулярна да бакавой грані прызмы, выходзіць з яе адхіленым на вугал δ = 45°. Паказчык праламлення шкла n = 1,55.
9. Прамень святла выходзіць з прызмы пад тым жа вуглом, пад якім ён на яе падае. Пры гэтым ён адхіляецца ад першапачатковага напрамку на вугал δ = 25°. Вызначыце паказчык праламлення n рэчыва прызмы, калі яе праламляльны вугал α = 45°
10. Адна з бакавых граней раўнабедранай прызмы пасярэбрана. Прамень святла падае нармальна на непасярэбраную грань і пасля двух адбіццяў выходзіць праз аснову прызмы перпендыкулярна да яе. Вызначыце вуглы прызмы.