§ 15. Інтэрферэнцыя святла
| Сайт: | Профильное обучение |
| Курс: | Фізіка. 11 клас |
| Падручнік: | § 15. Інтэрферэнцыя святла |
| Надрукаваны: | Гость |
| Дата: | Аўторак 1 Ліпень 2025 |
|
Імпульс цела можна скампенсаваць імпульсам, які мае процілеглы напрамак. А ці можна загасіць святло святлом? Пры якіх умовах два светлавыя пучкі пры накладанні адзін на аднаго ўтвораць цёмныя і светлыя палосы? Як ажыццявіць такі эксперымент? |
Прынцып суперпазіцыі электрычных палёў: напружанасць электрычнага поля сістэмы кропкавых зарадаў q1,q2, ..., qn у некаторым пункце прасторы роўна вектарнай суме напружанасцей палёў, якія ствараюцца ў гэтым пункце кожным з гэтых зарадаў паасобку, прычым поле кожнага не залежыць ад палёў іншых
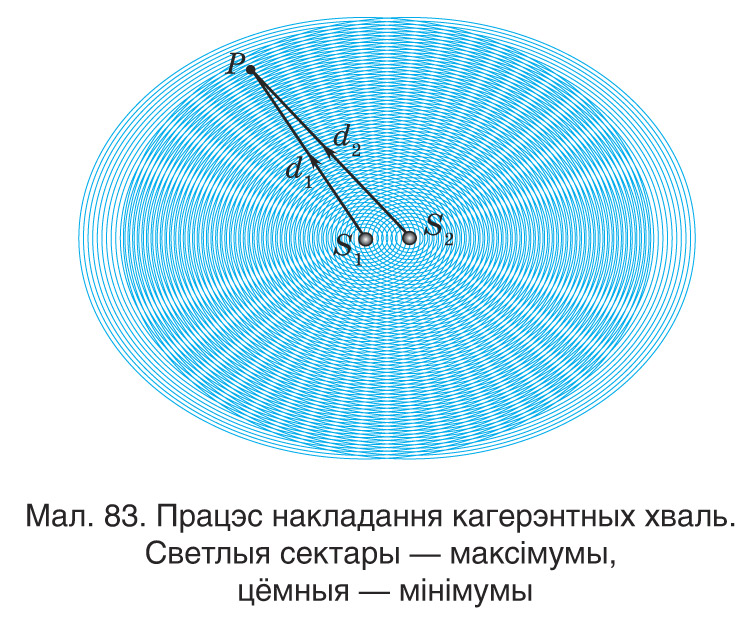
Разгледзім працэс накладання светлавых хваль даўжынёй λ, якія ўзбуджаюцца кропкавымі крыніцамі святла S1 і S2 (мал. 83). У тым абсягу, дзе гэтыя хвалі сустракаюцца, адбываецца іх накладанне.
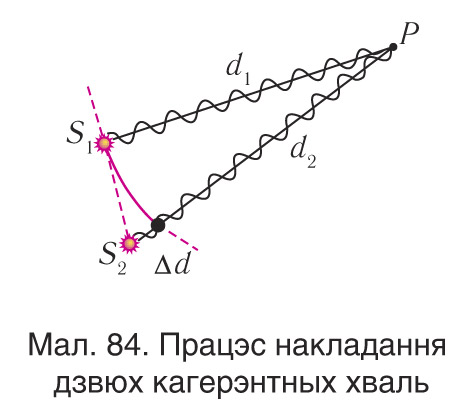
Паколькі светлавыя хвалі маюць электрамагнітную прыроду, для іх таксама, як і для электрычных і магнітных палёў выконваецца прынцып суперпазіцыі (ад лац. superposition — дадаванне). Паводле гэтага прынцыпу ваганні, выкліканыя хвалямі, складаюцца такім чынам, што выніковае электрамагнітнае поле роўна вектарнай суме палёў, створаных кожнай з іх: . Пры гэтым кожная з хваль распаўсюджваецца незалежна ад іншых. У абсягу, дзе хвалі перакрываюцца, узнікае даволі складаная карціна (гл. мал. 84). Аднак, выйшаўшы з гэтага абсягу, хвалі распаўсюджваюцца так, як быццам яны вольна «праходзяць адна скрозь адну» і пры гэтым ніяк не ўзаемадзейнічаюць паміж сабой.
Калі ў пункт P ад манахраматычных крыніц частатой ω прыйшлі дзве хвалі, што прайшлі розныя адлегласці d1 і d2 (мал. 84), то рознасць адлегласцей Δd=d2−d1 называюць рознасцю ходу. Паколькі пры рознасці ходу Δd=λ рознасць фаз Δφ=2π то можна скласці прапорцыю . З гэтай суадносіны знаходзім:
| (1) |
Такім чынам, рознасць фаз Δφ вызначаецца рознасцю ходу Δd
Хвалі аднолькавых частот, рознасць фаз ваганняў якіх у кожным пункце прасторы не змяняецца з цягам часу, называюцца кагерэнтнымі (ад лац. cohaerens — злучаны, счэплены). Адпаведна, уласцівасць, якая характарызуе ўзгодненасць праходжання ў прасторы і часе некалькіх вагальных ці хвалевых працэсаў, называецца кагерэнтнасцю.
Будзем меркаваць, што хвалі, якія прыходзяць, будуць мець у пункце P напружанасці электрычнага поля:
| (2) |
дзе E01, E02— амплiтуды, α1, α2— пачатковыя фазы ваганняў кожнай з хваль у пункце P.
Напружанасць выніковага электрычнага поля згодна з прынцыпам суперпазіцыі ў дадзеным пункце ў любы момант часу роўна вектарнай суме напружанасцей кожнай хвалі паасобку:
| (3) |
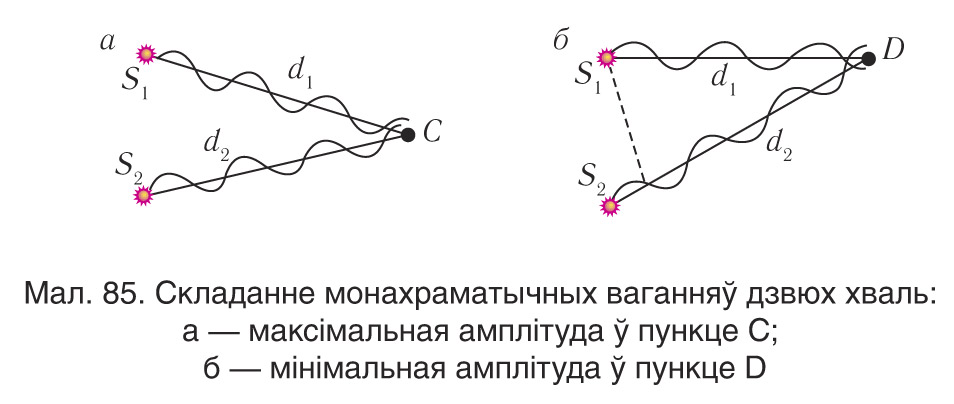
Калі рознасць ходу хваль ад крыніц S1 і S2 кратна даўжыні хвалі Δd=mλ, (m=0, 1, 2, ...), то і ваганні, што ўзбуджаюцца хвалямі ў пункце С (мал. 85, а), адбываюцца ў аднолькавай фазе. Пры гэтым грэбень адной хвалі накладваецца на грэбень другой.
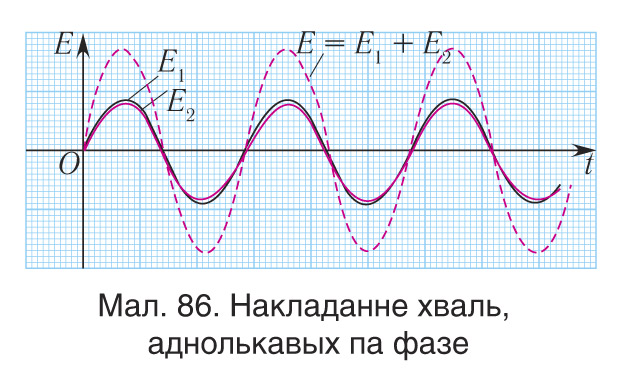
Адпаведна, амплітуда выніковага вагання ў пункце С роўна суме амплітуд хваль, якія накладваюцца, і аказваецца максімальнай (мал. 86):
| (4) |
Калі ж рознасць ходу хваль у пункце D (мал. 85, б) роўна няцотнаму ліку паўхваль , (m=0, 1, 2, ...), то
і ваганні адбываюцца ў проціфазе. Пры гэтым грэбень адной хвалі накладваецца на ўпадзіну другой.
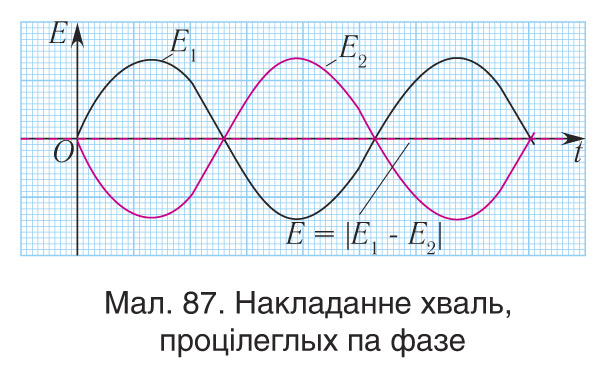
Такім чынам, у гэтым выпадку амплітуда выніковага вагання роўна модулю рознасці амплітуд хваль, якія накладваюцца, і аказваецца мінімальнай (мал. 87):
| (5) |
Заўважым, што ва ўсіх іншых пунктах амплітуда А выніковага вагання мае прамежкавае значэнне
Прыёмнікі выпраменьвання фіксуюць не саму светлавую хвалю, а энергію, прынесеную хваляй у дадзены абсяг прасторы. Параметрам, які характарызуе гэту энергію, з’яўляецца інтэнсіўнасць светлавой хвалі, якая абазначаецца лацінскай літарай I.
Паводле тэорыі электрамагнетызму інтэнсіўнасць электрамагнітнай хвалі прама прапарцыянальна квадрату амплітуды вектара напружанасці яе электрычнага поля Сімвал абазначае ўсярэдненне па часе. Аналагічнае ўсярэдненне можна зрабіць і для вектара індукцыі магнітнага поля
Зыходзячы з суадносін (4) і (5), бачна, што г. зн. інтэнсіўнасць выніковай хвалі не роўна суме інтэнсіўнасцей зыходных хваль. Гэта азначае, што хвалі інтэрферыруюць адна з адной.
З прычыны залежнасці рознасці фаз (1) ад пункта назірання ў прасторы атрымліваецца складаная карціна размеркавання інтэнсіўнасці выніковай хвалі. Устойлівае ў часе размеркаванне амплітуд ваганняў у прасторы пры інтэрферэнцыі называецца інтэрферэнцыйнай карцінай.
Такім чынам, інтэрферэнцыя (ад лац. inter — узаемна, паміж сабой і ferio — удараю, паражаю) — з’ява ўзнікнення ўстойлівай у часе карціны максімумаў і мінімумаў, што чаргуюцца, амплітуд выніковай хвалі пры складанні дзвюх (або некалькіх) кагерэнтных хваль.
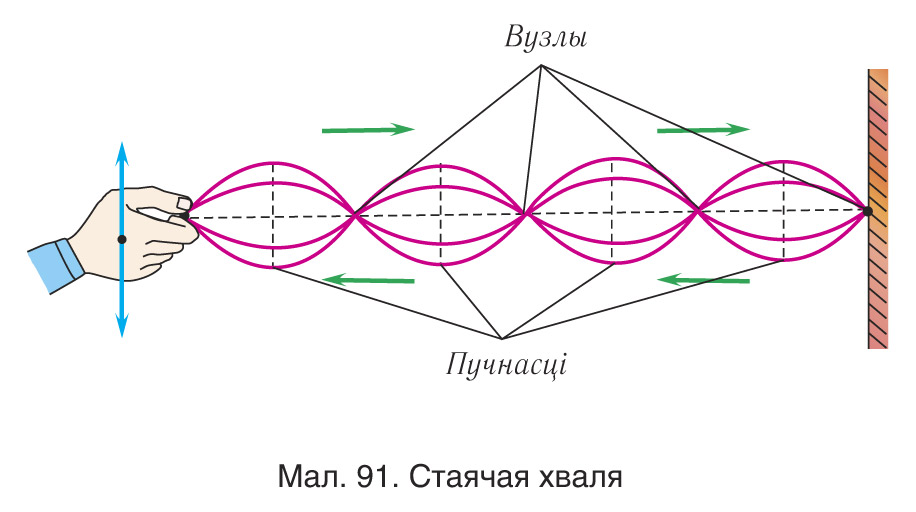
Падкрэслім, што заканамернасці інтэрферэнцыі справядлівыя для хваль любой прыроды (мал. 88) (электрамагнітных, гукавых, хваль на паверхні вады і г. д.), г. зн. носяць універсальны характар.
Пры разгляданні інтэрферэнцыі святла (электрамагнітных хваль) трэба ўлічыць, што даўжыня хвалі святла ў рэчыве змяняецца ў залежнасці ад паказчыку праламлення рэчыва. Калі адна хваля распаўсюджваецца ў рэчыве з паказчыкам праламлення n1, а другая — з паказчыкам праламлення n2, то рознасць фаз ваганняў:
дзе:
| (7) |
Тут δ — аптычная рознасць ходу хваль ад крыніц да пункту назірання, а велічыня nd — аптычная даўжыня шляху. Гэта велічыня вызначаецца адлегласцямі d1 і d2, пройдзенымі светлавымі хвалямі з улікам іх розных модулей скарасцей v2 і v1 распаўсюджвання ў гэтых асяроддзях з паказчыкамі праламлення n1 і n2.
Такім чынам, калі аптычная рознасць ходу (7) роўна цэламу ліку даўжынь хваль у вакууме, то ўмова максімуму інтэрферэнцыі:
|
|
(8) |
Хвалі прыходзяць у пункт P (гл. мал. 85) сінфазна, паколькі рознасць фаз у гэтым выпадку кратна 2π:
.
Калі аптычная рознасць ходу (7) роўна няцотнаму ліку паўхваль, то ўмова мінімуму інтэрферэнцыі:
|
|
(9) |
Хвалі прыходзяць у пункт P у проціфазе, і рознасць фаз ваганняў у гэтым выпадку роўна:
Для назірання інтэрферэнцыі святла неабходны кагерэнтныя крыніцы, якія выпраменьваюць хвалі з пастаяннай у часе рознасцю фаз. Распаўсюджаныя звычайныя крыніцы святла (лямпы напальвання, лямпы дзённага святла, свечкі і г. д.) не з’яўляюцца кагерэнтнымі. Для таго каб можна было назіраць ад іх інтэрферэнцыю святла, святло ад адной і той жа крыніцы неабходна падзяліць на два пучкі і затым звесці іх разам.

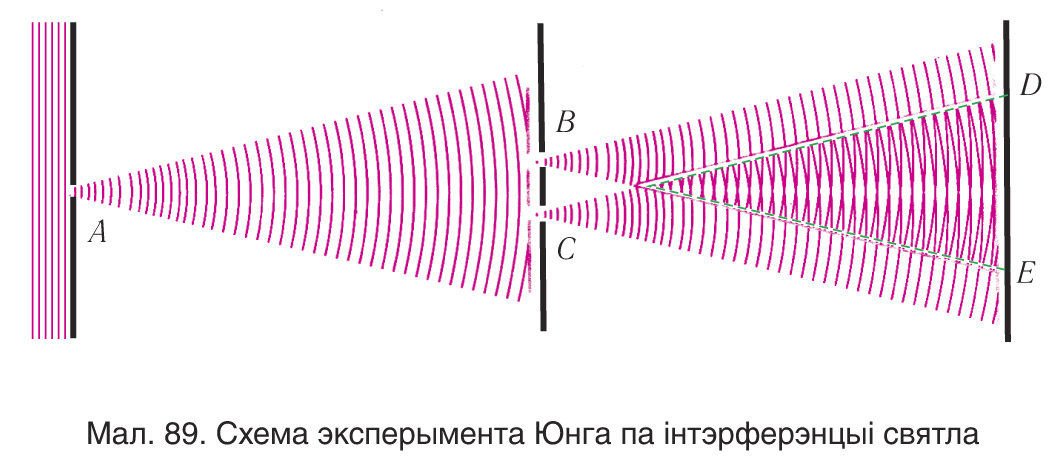
Для атрымання інтэрферэнцыйнай карціны карыстаюцца класічнай інтэрферэнцыйнай схемай (схемай Юнга), дзе пучок святла ад невялікай адтуліны А ў экране падзяляецца на два кагерэнтныя пучкі з дапамогай невялікіх адтулін В і С у наступным экране (мал. 89). Паколькі гэтыя пучкі створаны адной і той жа крыніцай А, яны з’яўляюцца кагерэнтнымі. Таму на трэцім экране ў абсягу DE перакрыцця пучкоў назіраецца інтэрферэнцыйная карціна.
Вынаходства і распаўсюджанне кагерэнтных крыніц выпраменьвання — лазераў — зрабіла дэманстрацыю з’явы інтэрферэнцыі досыць простай.
Найбольш вядомая праява інтэрферэнцыі, з якой мы часта сустракаемся ў паўсядзённым жыцці, — вясёлкавая афарбоўка мыльных бурбалак (мал. 90) ці тонкіх плёнак бензіну (нафты) на вадзе ці асфальце. Вясёлкавыя колеры ўзнікаюць на гэтых плёнках з прычыны інтэрферэнцыі святла, адбітага дзвюма паверхнямі плёнкі.
Пытаннi да параграфу
1. Што такое кагерэнтнасць? Якія хвалі называюцца кагерэнтнымі?
2. Што называюць інтэрферэнцыяй хваль? Пры якіх умовах адбываецца гэта з’ява?
3. Што называюць рознасцю ходу хваль? Аптычнай рознасцю ходу хваль?
4. Запішыце ўмовы ўтварэння інтэрферэнцыйных максімумаў і мінімумаў. Якой павінна быць аптычная рознасць ходу дзвюх хваль, каб іх інтэрферэнцыя прыводзіла да паслаблення (узмацнення) выніковага сігналу?
5. Чаму не ўзнікае інтэрферэнцыйная карціна ад святла дзвюх фар аўтамабіля?
6. Калі дзве хвалі інтэрферыруюць адна з адной, то ці ўплывае адна хваля на распаўсюджванне другой?
7. Чаму мыльная бурбалка на сонцы пераліваецца ўсімі колерамі вясёлкі?
8. Чаму ў тонкім слоі бензіну, які плавае на паверхні вады, узнікаюць вясёлкавыя палосы?
9. Чаму інтэрферэнцыйныя афарбоўка аднаго і таго ж месца паверхні мыльнай бурбалкі бесперапынна змяняецца?
10. Пры інтэрферэнцыі дзвюх хваль ці ўплывае адна хваля на напрамак распаўсюджвання другой?
Прыклад рашэння задачы
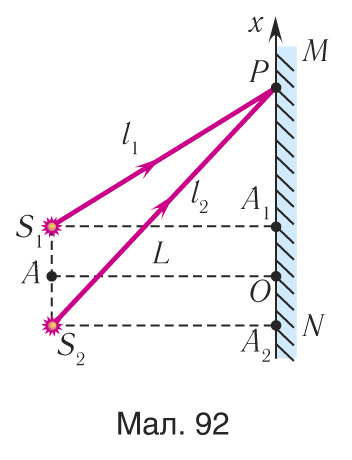
Вызначыце становішчы максімумаў і мінімумаў інтэрферэнцыйнай карціны на экране, які знаходзіцца на адлегласці L = AO = 2,0 м ад дзвюх аднолькавых кагерэнтных крыніц святла S1 і S2, размешчаных у вакууме на адлегласці d = 5,0 мм адна ад адной (мал. 92). Даўжыня хвалі выпраменьвання крыніц λ = 600 нм. Знайдзіце адлегласць Δx паміж суседнімі максімумамі.
L = 2,0 м,
λ = 600 нм =6,00·10-7 м.
Рашэнне:
Да некаторага пункта P на экране кожная з хваль праходзіць розны шлях l1 і l2. Максімум і мінімум будуць назірацца пры выкананні ўмоў, адпаведна:
δ = l2 - l1 = mλ,
З трохвугольнікаў ΔS1PA1 i ΔS2PA2, па тэараме Піфагора знаходзім:
| (1) | ||
| (2) |
дзе xm — каардыната пункта P.
Адкуль, адняўшы ад суадносіны (2) суадносіну (1), атрымаем:
З улікам таго, што d << L i l1 + l2 2L знаходзім:
З умовы максімумаў вынікае:
| |
Тады адлегласць ад цэнтра экрана да m-й светлай паласы знаходзіцца з суадносіны:
З умовы для мінімумаў знаходзім становішча цёмных палос
Адкуль:
Адлегласць паміж суседнімі максімумамі:
З атрыманай формулы бачна, што адлегласць Δx павялічваецца пры памяншэнні адлегласці d паміж кагерэнтнымі крыніцамі.
Адказ:
Практыкаванне 11
1. Што будзе назірацца ў некаторым пункце прасторы ў выніку інтэрферэнцыі дзвюх кагерэнтных хваль даўжынёй хвалі λ=400 нм аптычная рознасць ходу якіх δ=2,25 мкм?
2. Колькі даўжынь хваль N монахраматычнага выпраменьвання частатой ν=800 МГц змяшчаецца на адрэзку даўжынёй l = 2,0 м?
3. Экран MN асветлены кагерэнтнымі монахраматычнымі крыніцамі S1 і S2 (гл. мал. 92), перыяд ваганняў якіх T. Узмацненне ці паслабленне святла будзе назірацца ў пункце P, калі ад крыніцы S2 святло ў яго прыходзіць пазней на прамежак часу τ=2,5T чым ад крыніцы S1?
4. Дзве кагерэнтныя хвалі, даўжыні хваль якіх λ=404 нм, прыходзяць у адзін пункт на экране. Што будзе назірацца ў гэтым пункце (узмацненне ці паслабленне святла), калі аптычная рознасць ходу роўна δ=17,17 мкм?
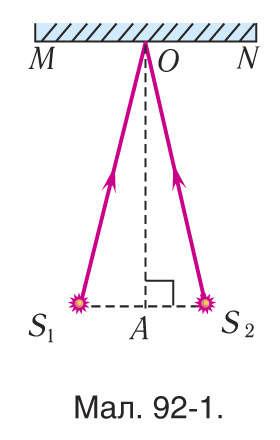
5. Дзве кагерэнтныя крыніцы белага святла S1 і S2 асвятляюць экран MN, плоскасць якога паралельна адрэзку S1S2 (мал. 92-1). Дакажыце, што ў пункце O будзе максімум асветленасці, калі S1O=S2O.
6. Ва ўстаноўцы Юнга адлегласць паміж шчылінамі d=1,5 см, экран размешчаны на адлегласці l=2,0 м ад шчылін. Шчыліны асвятляюцца монахраматычнай крыніцай, даўжыня хвалі якой λ=687 нм. Вызначыце адлегласць Δx паміж інтэрферэнцыйнымі палосамі на экране.
7. На экран А ад кропкавай крыніцы, якая знаходзіцца на вялікай адлегласці ад яго, падае святло. У экране ёсць дзве паралельныя шчыліны на адлегласці адна ад адной. На экране В, размешчаным на адлегласці l=1,0 паралельна экрану А, адлегласці паміж інтэрферэнцыйнымі палосамі
. Вызначыце даўжыню хвалі выпраменьвання