§ 2. Спружынны і матэматычны маятнікі
| Сайт: | Профильное обучение |
| Курс: | Фізіка. 11 клас |
| Книга: | § 2. Спружынны і матэматычны маятнікі |
| Напечатано:: | Гость |
| Дата: | Четверг, 3 Июль 2025, 07:59 |
|
Груз, падвешаны на нітцы, які вагаецца ў полі цяжару Зямлі, а таксама груз, прымацаваны да спружыны — прыклады найбольш простых механічных вагальных сістэм. Разгледзім фізічныя працэсы, якія адбываюцца ў такіх сістэмах. |
Сукупнасць некалькіх цел утвараюць механічную сістэму. Целы, якія не ўваходзяць у сістэму, называюцца знешнімі.
Другі закон Ньютана (асноўны закон дынамікі): паскарэнне, якое набывае цела пад дзеяннем прыкладзеных да яго сіл, адваротна прапарцыянальна масе цела, накіравана па выніковай гэтых сіл і прама прапарцыянальна яе модулю:
Закон Гука: пры пругкіх дэфармацыях сціскання і расцяжэння модуль сілы пругкасці прама прапарцыянальны модулю змянення даўжыні цела:
дзе k — жорсткасць цела, l0 — даўжыня недэфармаванага цела, l — даўжыня дэфармаванага цела. Напрамак сілы пругкасці заўсёды процілеглы напрамку зруху пры дэфармацыі.
Якія ўмовы неабходны для ўзнікнення ваганняў?
Вынікі доследаў паказваюць, што для ўзнікнення і існавання механічных ваганняў цела першапачаткова неабходна прывесці ў рух. Гэта можна зрабіць, адхіліўшы яго ад становішча раўнавагі ці надаўшы яму пачатковую скорасць пасродкам штуршка. Гэтым адхіленнем ці штуршком вызначаецца амплітуда ваганняў. Акрамя таго, пры вывядзенні цела са становішча раўнавагі ў вагальнай сістэме павінна ўзнікаць выніковая сіла, якая імкнецца вярнуць цела ў становішча раўнавагі.
Найпрасцейшая вагальная сістэма, якая складаецца з цела з прымацаванай да яго спружынай, што злучае цела і апору, называецца спружынным маятнікам. Спружына можа размяшчацца як гарызантальна (гарызантальны спружынны маятнік), так і вертыкальна (вертыкальны спружынны маятнік).
Разгледзім ваганні гарызантальнага спружыннага маятніка.
 Няхай цела масай m, што ляжыць на гладкай гарызантальнай паверхні, прымацавана да свабоднага канца бязважкай спружыны жорсткасцю k (мал. 13, а). Другі канец спружыны прымацаваны да нерухомай апоры.
Няхай цела масай m, што ляжыць на гладкай гарызантальнай паверхні, прымацавана да свабоднага канца бязважкай спружыны жорсткасцю k (мал. 13, а). Другі канец спружыны прымацаваны да нерухомай апоры.
Выведзем цела са становішча раўнавагі, зрушыўшы яго, напрыклад, управа на адлегласць x (гл. мал. 13, б). Пры гэтым згодна з законам Гука ўзнікне сіла пругкасці прыкладзеная да цела і накіраваная ўлева.
Згодна з другім законам Ньютана будзе выконвацца роўнасць:
|
|
(1) |
З улікам закона Гука з (1) атрымліваем ураўненне для праекцый велічынь на вось Ox (гл. мал. 13, б):
|
|
(2) |
Згодна з (2) паскарэнне цела масай m прапарцыянальна дзеючай сіле і накіравана да становішча раўнавагі. Пры гэтым узнікаюць ваганні цела. Кожныя паўперыяды напрамак руху змяняецца на процілеглы. Зрух грузу адбываецца то ўправа, то ўлева адносна становішча раўнавагі, г. зн. ён мяняе знак. Такім чынам, і праекцыя сілы згодна з (2) таксама мяняе знак.
Перапішам атрыманую суадносіну (2) у выглядзе:
|
|
(3) |
Ураўненне (3) называецца ўраўненнем гарманічных ваганняў спружыннага маятніка.
Такім чынам, неабходнай умовай узнікнення гарманічных ваганняў з’яўляецца дзеянне вяртальнай сілы, накіраванай да становішча раўнавагі і прама прапарцыянальнай зруху цела ад становішча раўнавагі. Гэта вяртальная сіла заўсёды накіравана да становішча раўнавагі, аб чым «гаворыць» мінус ва ўраўненні (2).
У становішчы раўнавагі вяртальная сіла роўна нулю (F = 0), паколькі x = 0. Таму калі ў гэтым становішчы цела, што вагаецца, спыніць, то ваганні знікнуць.
Разлікі паказваюць, а вынікі эксперыментаў пацвярджаюць, што пры апісаных умовах цела будзе выконваць ваганні з перыядам:
|
|
(4) |
З улікам таго, што перыяд звязаны з цыклічнай частатой суадносінай , знаходзім:
| (5) |
 З формул (4) і (5) вынікае, што перыяд і частата гарманічных ваганняў спружыннага маятніка вызначаюцца масай грузу m і жорсткасцю спружыны k і не залежаць ад амплітуды яго ваганняў.
З формул (4) і (5) вынікае, што перыяд і частата гарманічных ваганняў спружыннага маятніка вызначаюцца масай грузу m і жорсткасцю спружыны k і не залежаць ад амплітуды яго ваганняў.
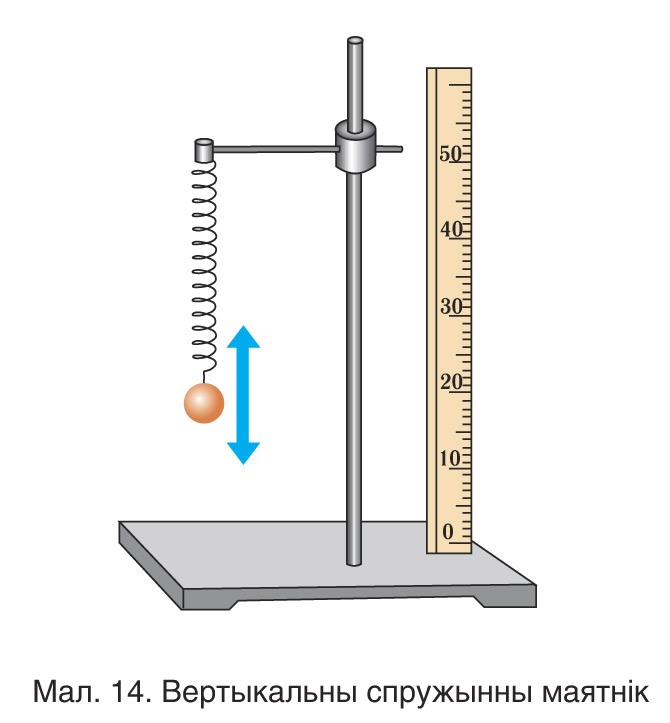
Адзначым, што перыяд і цыклічная частата ваганняў вертыкальнага спружыннага маятніка (мал. 14) таксама вызначаюцца па формулах (4) і (5).
Адной з найбольш распаўсюджаных вагальных сістэм з’яўляецца матэматычны маятнік.
Матэматычным маятнікам называецца невялікае цела масай m, падвешанае на бязважкай нерасцяжной нітцы даўжынёй l, якое знаходзіцца ў полі сілы цяжару (мал. 15).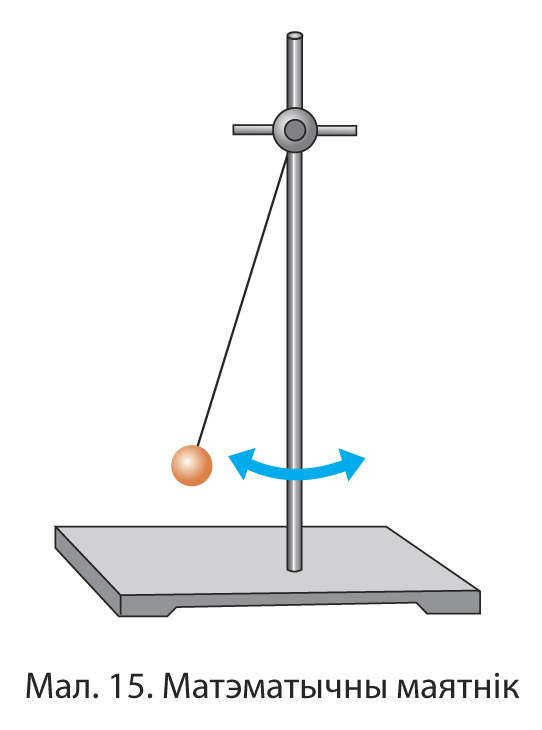
Разгледзім ваганні матэматычнага маятніка.
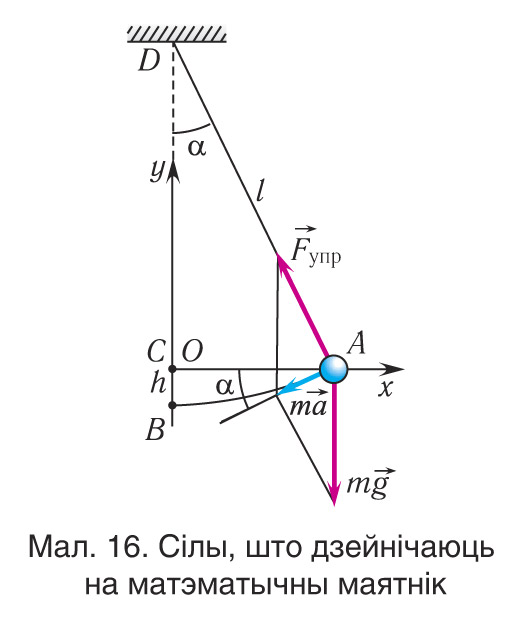
Адхіленне маятніка ад становішча раўнавагі будзем характарызаваць вуглом a (мал. 16), які ўтварае нітка з вертыкаллю. Пасля адхілення маятніка ад становішча раўнавагі на яго дзейнічаюць дзве сілы: накіраваная вертыкальна ўніз сіла цяжару і накіраваная ўздоўж ніткі сіла пругкасці
Пад дзеяннем гэтых сіл цела рухаецца паскорана да становішча раўнавагі (пункт B). Прайшоўшы пункт B, цела працягвае рухацца, але яго скорасць паступова памяншаецца, ператвараючыся ў нуль у пункце, сіметрычным пункту А адносна вертыкалі. Пасля гэтага яно пачынае рухацца назад да пункта B.
Згодна з другім законам Ньютана для руху маятніка можам запісаць:
| (6) |
У праекцыях на выбраныя восі каардынат Ox і Oy (гл. мал. 16) атрымліваем:
| (7) |
| (8) |
Паколькі пры малых вуглах адхілення даўжыня дугі АВ ≈ х, то з ΔAOD знаходзім:
дзе х — адхіленне маятніка ад становішча раўнавагі, l — даўжыня маятніка. Падставіўшы выраз для сінуса ў (7), атрымаем:
| (9) |
Такім чынам, сілай, якая вяртае маятнік да ўстойлівага становішча раўнавагі пры ваганнях, з’яўляецца раўнадзейная сіл пругкасці яго ніткі і цяжару.
Пры малых вуглах адхілення маятніка праекцыя вектара паскарэння і яе можна не ўлічваць, а
, тады з ураўнення (8) вынікае Fпр ≈ mg. Значыць, ураўненне руху маятніка ўздоўж восі Ox запішацца ў выглядзе:
дзе ax — праекцыя паскарэння, якое надаецца грузу маятніка сілай пругкасці ніткі. Такім чынам атрымліваем ураўненне ваганняў матэматычнага маятніка:
|
|
(10) |
Параўнаўшы суадносіны (10), (3) і (5), лёгка атрымаць формулу для цыклічнай частаты матэматычнага маятніка ў полі цяжару Зямлі:
| (11) |
Перыяд малых ваганняў матэматычнага маятніка у полі цяжару Зямлі вызначаецца па формуле Гюйгенса:
|
|
(12) |
Выкарыстаўшы суадносіны (4) і (11), ураўненні ваганняў спружыннага маятніка і матэматычнага маятніка
можна запісаць у аднолькавым выглядзе:
| (13) |
Такім чынам, залежнасці каардынат ад часу x(t), якія апісваюцца ўраўненнямі (5) і (6) з § 1, задавальняюць ураўненне (13), якое называецца ўраўненнем гарманічных ваганняў.
Як бачна з формул (11), (12), перыяд і цыклічная частата малых ваганняў матэматычнага маятніка не залежаць ад масы маятніка і амплітуды яго ваганняў, а вызначаюцца толькі яго даўжынёй і паскарэннем свабоднага падзення.
Галілеа Галілей першы эксперыментальна вызначыў, што перыяд малых ваганняў () матэматычнага маятніка даўжынёй l у полі сілы цяжару не залежыць ад яго масы m і амплітуды ваганняў (вугла пачатковага адхілення a).
  |
Адным з найважнейшых дасягненняў Хрысціяна Гюйгенса было вынаходства гадзінніка з маятнікам. Ён запатэнтаваў сваё вынаходства 16 ліпеня 1657 г. У 1673 г. пабачыла свет яго праца «Маятнікавы гадзіннік», у якой былі выкладзены тэарэтычныя асновы яго вынаходства. Менавіта пастаянства перыяду (частаты) ваганняў маятніка дазволіла выкарыстаць яго для стварэння гадзінніка.
Калі маятнік набывае дадатковае паскарэнне , абумоўленае, напрыклад, паскораным рухам пункта падвесу, то пры гэтым будзе змяняцца сіла пругкасці ніткі. У такім выпадку перыяд ваганняў маятніка будзе вызначацца па формуле
дзе — «эфектыўнае паскарэнне», роўнае вектарнай рознасці
.
Павышаная цікавасць да гарманічных ваганняў тлумачыцца тым, што яны шырока распаўсюджаны ў навуцы і тэхніцы (маятнікі, музычныя інструменты, святло, пераменныя токі і г. д.). Акрамя таго, гарманічныя ваганні маюць простае матэматычнае апісанне, а іх перыяд не залежыць ад амплітуды. Падкрэслім, што любы перыядычны рух можна разглядаць як вынік накладання простых гарманічных складаемых.
Уласцівасць незалежнасці перыяду ваганняў маятніка ід амплітуды называецца ізахроннасцю (ад грэч. εσος (ізас) — роўны і χρονος (хронас) — час). Такім чынам, ваганні спружыннага маятніка маюць уласцівасць ізахроннасці. Ізахроннасць ваганняў маятніка была адкрыта Галілеа Галілеем у 1583 г. пры вывучэнні руху грузу, падвешанага на нітцы.
Пытаннi да параграфу
1. Які маятнік называюць спружынным? Запішыце кінематычны закон руху спружыннага маятніка.
2. Па якой формуле вызначаецца цыклічная частата ваганняў спружыннага маятніка? Перыяд яго ваганняў?
3. Ці зменіцца перыяд ваганняў спружыннага маятніка, калі яго «перанесці» з паверхні Зямлі на паверхню Месяца? Прывесці ў стан бязважкасці?
4. Які маятнік называюць матэматычным? Запішыце кінематычны закон руху матэматычнага маятніка.
5. Як накіравана раўнадзейная сіл, прыкладзеных да грузу маятніка, у моманты, калі ён знаходзіцца ў крайніх становішчах? Калі праходзіць праз становішча раўнавагі?
6. Маятнікавы гадзіннік спяшаецца. Як трэба змяніць даўжыню падвеса, каб ён ішоў дакладна?
7. Якім чынам, выкарыстаўшы матэматычны маятнік, можна вызначыць паскарэнне свабоднага падзення ў дадзеным месцы?
8. Ці ўплывае змяненне тэмпературы на дакладнасць ходу маятнікавага гадзінніка?
Прыклад рашэння задачы
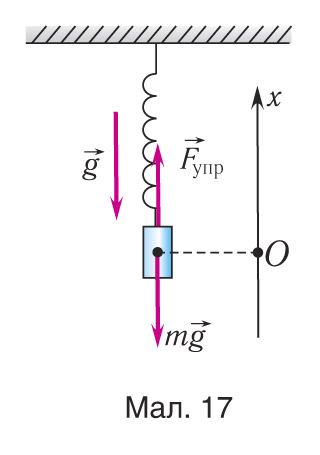
1. Вызначыце цыклічную частату і перыяд ваганняў T цела, масай m = 500 г, прымацаванага да вертыкальнай спружыны (мал. 17). Вядома, што ў стане спакою цела расцягвае спружыну на адлегласць х0 = 10 мм і для ўзбуджэння ваганняў яго зрушваюць уніз на адлегласць х = 30 мм і адпускаюць.
m = 500 г = 0,500 кг
х = 30 мм = 3,0 · 10−2 м
х0 = 10 мм = 1,0 · 10−2 м
Рашэнне
Цыклічная частата ваганняў вертыкальнага спружыннага маятніка, таксама як і гарызантальнага, вызначаецца па формуле:
Знойдзем жорсткасць k спружыны. З умовы раўнавагі цела вынікае:
Па законе Гука ў праекцыі на вось Ох маем:
Тады ў праекцыі на вось Ox умова раўнавагі запішацца:
Перыяд ваганняў знаходзім з суадносіны:
Адказ: .
2. Выведзіце формулу для перыяду Т ваганняў вертыкальнага спружыннага маятніка, калі маса грузу m і жорсткасць спружыны k.
Рашэнне
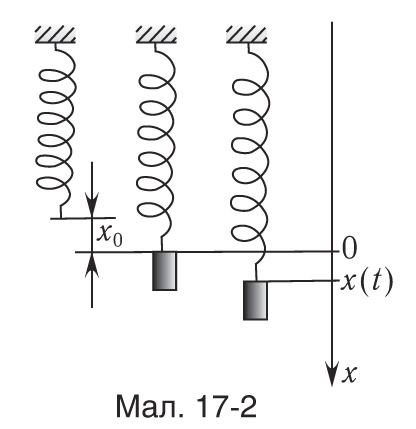
Разгледзім вертыкальны рух грузу, які адбываецца пад дзеяннем сілы пругкасці спружыны і сілы цяжару грузу пасля штуршка (мал. 17-1). Пачатак каардынат змесцім у пункт, які адпавядае раўнаважнаму становішчу цела (мал. 17-2). У гэтым становішчы спружына расцягнута на велічыню x0, вызначаемую суадносінай:
| (1) |
 |
 |
.
Пры зрушэнні грузу на велічыню x са становішча раўнавагі сіла, якая дзейнічае з боку спружыны на груз, роўна .
Тады па другім законе Ньютана .
С учетом соотношения (1) это уравнение перепишем в виде:
Калі ўвесці абазначэнне , то ўраўненне руху грузу запішацца ў выглядзе:
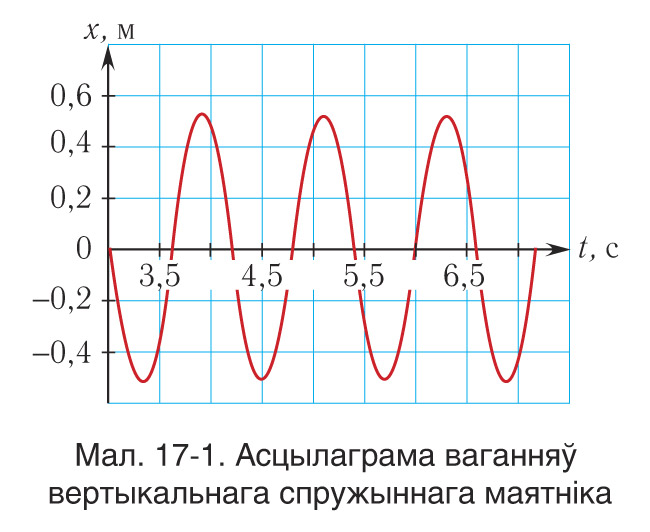
Яно апісвае гарманічныя ваганні вертыкальнага спружыннага маятніка з частатой, такой самай як у гарызантальнага спружыннага маятніка. Значыць, перыяд ваганняў вертыкальнага спружыннага маятніка вызначаецца па такой жа формуле, як і гарызантальнага. Гэта пацвярджаецца і запісам асцылаграмы ваганняў вертыкальнага спружыннага маятніка (мал. 17-1).
Адказ: . Такім чынам, дзеючая ў вагальнай сістэме пастаянная сіла зрушвае становішчы раўнавагі, але не змяняе частату ваганняў.
Практыкаванне 2
1. Вызначыце перыяд Т і частату ваганняў грузу масай m = 200 г, падвешанага на спружыне жорсткасцю
2.Вызначыце даўжыню l матэматычнага маятніка каля паверхні Зямлі, калі частата яго ваганняў = 1,0 Гц.
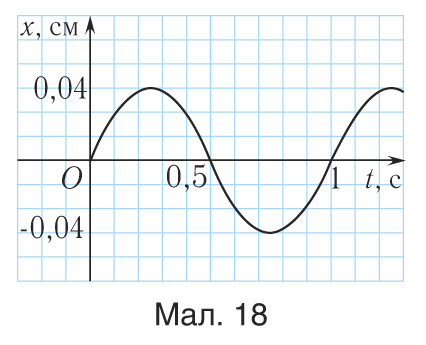
3. Вызначыце жорсткасць k спружыны маятніка масай m = 400 г, які выконвае ваганні, паказаныя на малюнку 18.
4.Груз, падвешаны да спружыны, выклікае яе падаўжэнне на велічыню Δl. Вызначыце Δl.спружыны, калі цыклічная частата вертыкальных ваганняў такой сістэмы
5.Два целы з аднолькавымі масамі падвешаны да дзвюх аднолькавых спружын. Целы зрушваюць уніз: адно на адлегласць x1 = 10 см, другое — на х2 = 20 см ад становішча раўнавагі, затым адначасова адпускаюць. Якое з іх першым пройдзе становішча раўнавагі?
6.Адзін матэматычны маятнік выканаў за некаторы час N1 = 20 ваганняў, а другі за той жа час выканаў N2 = 16 ваганняў. Вызначыце даўжыню l2 другога маятніка, калі вядома, што рознасць даўжынь маятнікаў Δl= 10 см.
7.Перыяд малых ваганняў матэматычнага маятніка на паверхні Зямлі роўны Т = 0,80 с. Якім будзе перыяд Т1 яго ваганняў каля паверхні Марса, калі паскарэнне свабоднага падзення gм = 0,37gз?
8.Вызначыце даўжыню l секунднага маятніка, усталяванага ў Мінску, дзе паскарэнне свабоднага падзення Знайдзіце адносную хібнасць разліку, у якім паскарэнне свабоднага падзення было б прынята роўным
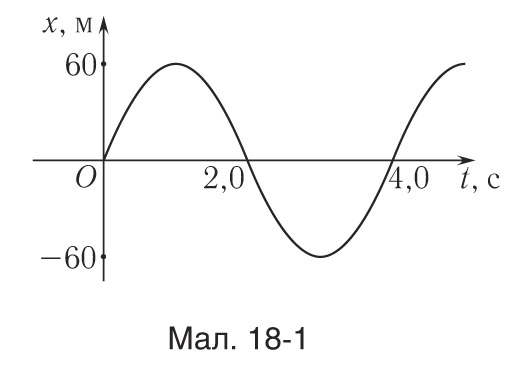
9.Вызначыце даўжыню l матэматычнага маятніка, які выконвае ваганні, паказаныя на малюнку 18-1.
10.На спружыне вагаецца груз з частатой = 0,620 Гц. Калі да яго прымацавалі дадатковы груз масай
, частата ваганняў стала
1 = 480 Гц. Знайдзіце масу m пачатковага грузу.
11.Цела масай m падвешана на спружыне жорсткасцю k . Спружыну разрэзалі напалам і прымацавалі да яе адной паловы тое ж цела. У колькі разоў n змянілася частата ваганняў гэтага цела??
12.Дзве бязважкія спружыны жорсткасцямі і
злучаны адзін раз паслядоўна, другі — паралельна. У колькі разоў n будуць адрознівацца перыяды ваганняў грузу на такіх спружынах?