§ 1-1. Ураўненне гарманічных ваганняў
| Сайт: | Профильное обучение |
| Курс: | Фізіка. 11 клас |
| Падручнік: | § 1-1. Ураўненне гарманічных ваганняў |
| Надрукаваны: | Госць |
| Дата: | Серада 2 Ліпень 2025 |
|
Пры руху матэрыяльнага пункта (МП) па акружнасці радыусам R з пастаянняй вуглавой скорасцю Цэнтраімклівае паскарэнне МП накіравана да цэнтра акружнасці і яго модуль роўны |
 Вынікі эксперыментаў паказваюць, што для ўзнікнення і існавання механічных ваганняў неабходна выкананне пэўных умоў. Перш за ўсё, пры вывядзенні (напрыклад, пры малым зрушэнні) цела са становішча раўнавагі ў сістэме павінна ўзнікаць выніковая сіла, якая імкнецца вярнуць цела ў становішча раўнавагі. Акрамя таго, у сістэме павінна быць дастаткова малое трэнне, паколькі ў адваротным выпадку ваганні хутка затухнуць з прычыны страты энергіі або нават могуць не ўзнікнуць увогуле.
Вынікі эксперыментаў паказваюць, што для ўзнікнення і існавання механічных ваганняў неабходна выкананне пэўных умоў. Перш за ўсё, пры вывядзенні (напрыклад, пры малым зрушэнні) цела са становішча раўнавагі ў сістэме павінна ўзнікаць выніковая сіла, якая імкнецца вярнуць цела ў становішча раўнавагі. Акрамя таго, у сістэме павінна быць дастаткова малое трэнне, паколькі ў адваротным выпадку ваганні хутка затухнуць з прычыны страты энергіі або нават могуць не ўзнікнуць увогуле.
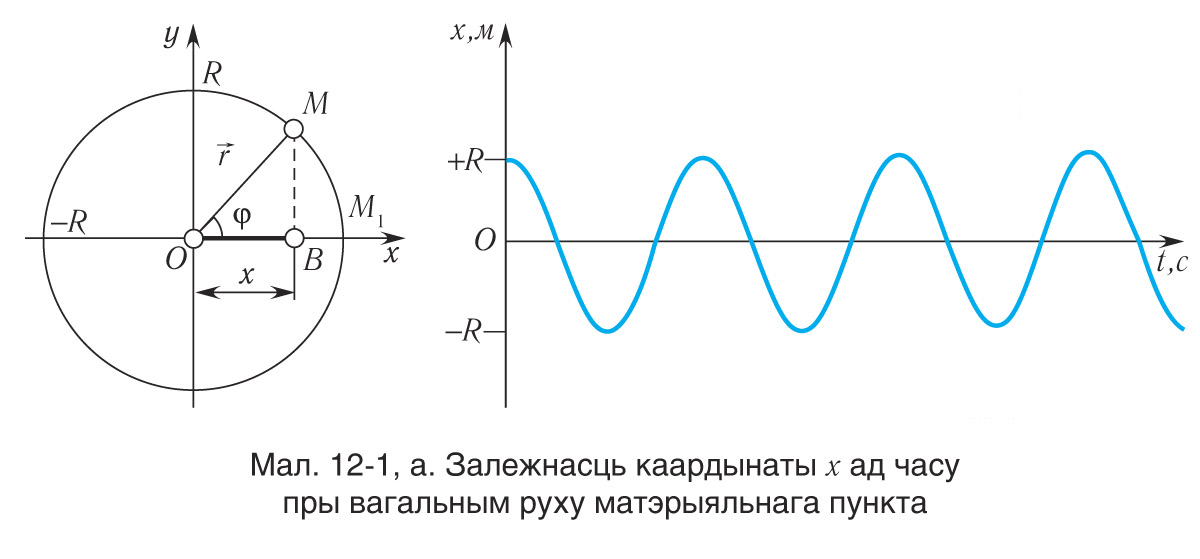
Разгледзім вывучаны вамі ў 9-м класе выпадак перыядычнага руху — раўнамернае вярчэнне цела па акружнасці. Будзем лічыць цела матэрыяльным пунктам (МП), яно верціцца ў плоскасці ху па акружнасці радыусам R з лінейнай скорасцю (гл. мал. 12-1, а). Няхай разглядаемы рух адбываецца супраць ходу гадзіннікавай стрэлкі. Выберам восі Ох и Оу, як паказана на малюнку 12-1, а.
Калі ў пачатковы момант часу t0 = 0 матэрыяльны пункт знаходзіўся ў становішчы М1, то праз прамежак часу ён апынецца ў некаторым становішчы М. Спраецыруем на вось Ох радыус-вектар
пункта, які рухаецца, яго лінейную скорасць
и цэнтраімклівае паскарэнне
.
Праекцыя радыус-вектара на вось Ох з’яўляецца яго каардынатай х (пункт В). Яна вызначае зрушэнне матэрыяльнага пункта ад цэнтра акружнасци О ўздоўж восі Ох (мал. 12-1, а).
Паколькі пры раўнамерным вярчэнні пункта М па акружнасці яго каардыната (зрушэнне) х будзе перыядычна змяняцца ад да
, то можна сказаць, што пункт В выконвае вагальны рух уздоўж восі Ох, а яго каардыната х з’яўляецца каардынатай вагальнага пункта.
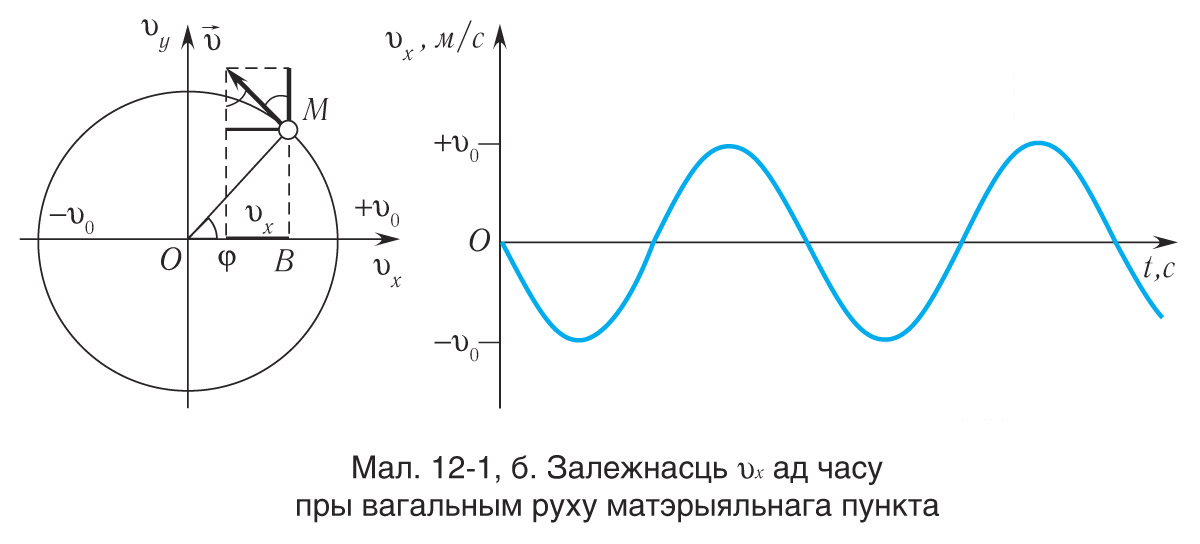
Адпаведна, праекцыя лінейнай скорасці матэрыяльнага пункта М на вось Ох з’яўляецца праекцыяй скорасці
пункта В і перыядычна змяняецца ад
да
(гл. мал. 12-1, б). Праекцыя цэнтраімклівага паскарэння МП
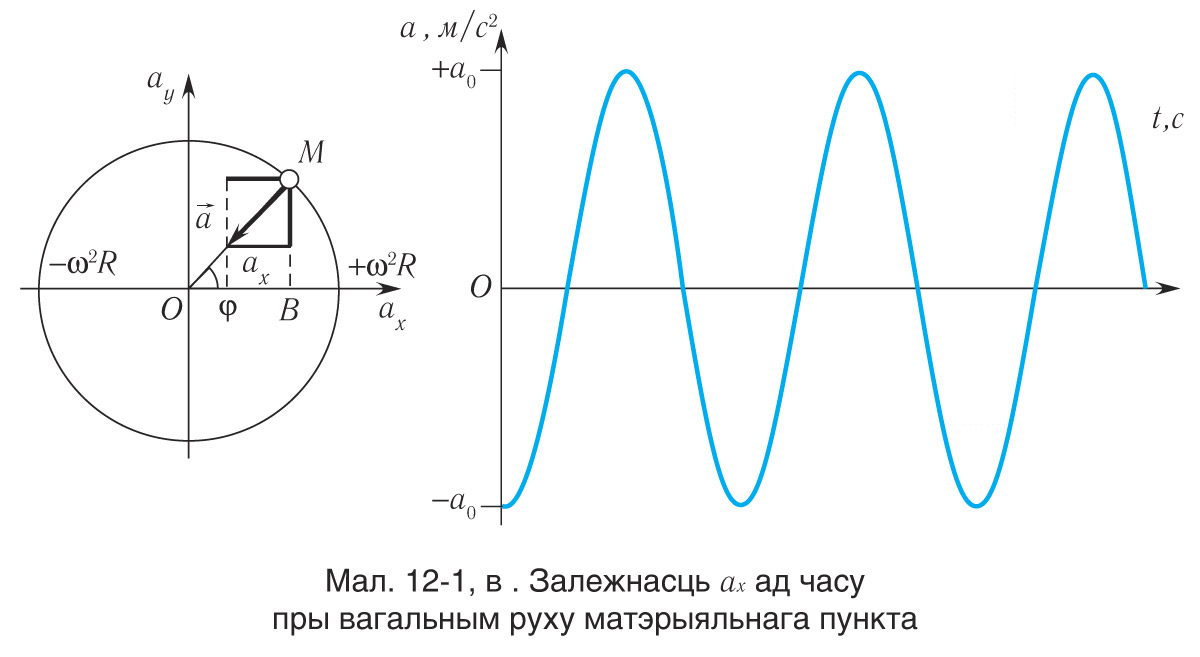
на вось Ох (гл. мал. 12-1, в) з’яўляецца праекцыяй паскарэння
пункта В, якое таксама перыядычна змяняецца ад
да
.
 |
 |
Радыус-вектар за прамежак часу
павярнуўся на вугал
(гл. мал. 12-1, а). Пры раўнамерным вярчэнні пункта па акружнасці яго лінейная скорасць
накіравана па датычнай (гл. мал. 12-1, б), а цэнтраімклівае паскарэнне
— да цэнтра акружнасці (гл. мал. 12-1, в). Такім чынам:
З улікам таго, што модуль лінейнай скорасці v0=ωR і модуль цэнтраімклівага паскарэння и
, выконваюцца суадносіны:
дзе T — перыяд вярчэння цела па акружнасці.
Калі ў момант часу t = t0 = 0 матэрыяльны пункт знаходзіўся ў пункце М1, то каардынату vx, праекцыі скорасці і паскарэння ах пункта В у любы момант часу можна вызначыць па формулах:
|
|
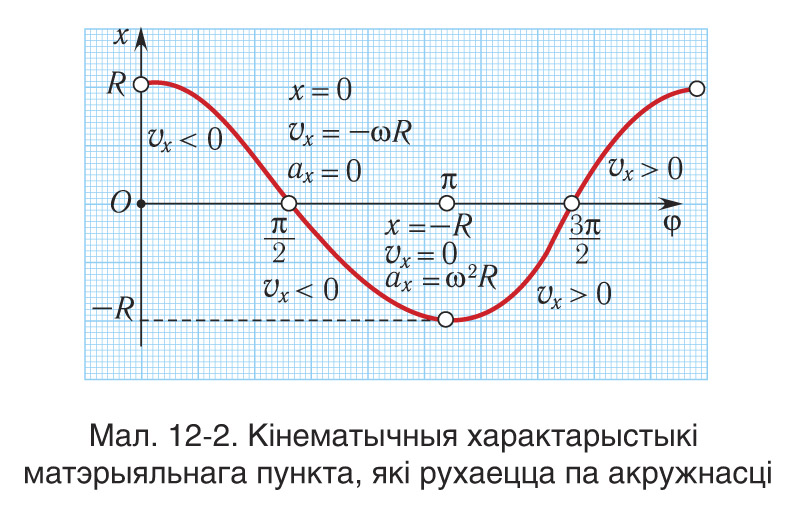 Поскольку функции
Поскольку функции периодические, то через промежуток времени равный периоду T , по истечении которого угол
изменится на
, все характеристики движения точки B вдоль оси
(координата, проекции скорости и ускорения) примут прежние значения (см. таблицу 1-1, рис. 12-1), т. е. значения характеристик периодически повторяются.
Точка B в течение этого промежутка времени дважды проходит через начало координат, двигаясь в противоположных направлениях вдоль оси (рис. 12-2). Как отмечалось выше, повторяемость — основной признак периодического движения
|
Табліца 1-1. Каардыната х, праекцыі скорасці |
|||
| t | x | vx | ax |
| 0 | R | O | - a0 |
| 0 | - vo | 0 | |
| - R | 0 | a0 | |
| 0 | v0 | 0 | |
| T | R | 0 | - a0 |
Звернем увагу на тое, што праекцыя паскарэння
пункта В (гл. мал. 12-1 а, в) у любы момант часу прапарцыянальна зрушэнню (каардынаце)
і процілегла яму па знаку:
Перапішам дадзеную суадносіну ў выглядзе:
| (1) |
Такім чынам, ваганні, што апісваюцца ўраўненнем (1), з’яўляюцца гарманічнымі, паколькі іх рашэннямі з’яўляюцца функцыі синуса або косінуса. Ураўненне (1) называецца ўраўненнем гарманічных ваганняў. Сістэма, якая выконвае такія ваганні, — гарманічнай вагальнай сістэмай або гарманічным асцылятарам (ад лац. оscillo — вагаюся).
Ураўненню гарманічных ваганняў адпавядаюць залежнасці (5) або (6) (гл. § 1), якія называюцца кінематычным законам руху пры гарманічных ваганнях.
Пры разгляданні ваганняў важнае значэнне мае велічыня, якая стаіць пад знакам сінуса або косінуса ў (2) і (3) і называецца фазай ваганняў. Такім чынам, фаза (ад грэч. (фазіс) — з’яўленне, момант з’яўлення) — аргумент перыядычнай функцыі, які вызначае значэнне фізічнай велічыні ў любы момант часу t. Яна вызначае стан вагальнай сістэмы (каардынаты, скорасці, паскарэнні) у любы момант часу пры зададзенай частаце і амплітудзе. Адзінкай фазы з’яўляецца радыян (1 рад);
— пачатковая фаза, якая вызначае стан вагальнай сістэмы ў пачатковы момант часу (t0 = 0).
Амплітуда ваганняў А і пачатковая фаза вызначаюцца не ўласцівасцямі самой сістэмы, а тым спосабам, якім у сістэме выкліканы ваганні. Так, ваганні можна выклікаць адхіленнем ад стану раўнавагі, а можна — штуршком са стану раўнавагі.
Заўважым, што гэтаксама як мы разглядалі змяненне каардынаты х цела М, якое верціцца, можна разглядаць і змяненне яго каардынаты у (пункт С) (гл. мал. 12-1, а). Значыць, пункт С будзе выконваць гарманічныя ваганні ўздоўж восі Оу.
Такім чынам, раўнамернае вярчэнне цела па акружнасці можна разглядаць як накладанне двух аднолькавых па амплітудзе гарманічных ваганняў, якія адбываюцца адначасова ў двух узаемна перпендыкулярных напрамках.
Пытанні да параграфу
- У якія моманты часу ператвараецца ў нуль паскарэнне гарманічнага асцылятара?
- Што называецца фазай гарманічнага вагання? Пачатковай фазай гарманічнага вагання?
- Ці могуць у якісьці момант часу супасці напрамкі зрушэння і скорасці гарманічнага асцылятара?
- Ці можна падвоіць, патроіць максімальную скорасць гарманічнага асцылятара?
Прыклад рашэння задачы
За якую частку перыяду цела, якое выконвае гарманічныя ваганні, прахоздіць адлегласць: а) ад становішча раўнавагі да максімальнага зрушэння; б) першую палову гэтай адлегласці; в) другую палову гэтай адлегласці?
Рашэнне
Каардыната х цела, якое выконвае гарманічныя ваганні, вызначаецца суадносінай:
.
Тут A — амплітуда ваганняў, t — час, які адлічваецца з моманту праходжання становішча раўнавагі, T — перыяд ваганняў, — пачатковая фаза.
Няхай цела знаходзіцца ў становішчы раўнавагі ў пачатковы момант часу , тады
і
.
а) Прамежак часу , неабходны целу для праходжання адлегласці з сярэдняга становішча ў крайняе
, вызначаецца з ураўнення:
Найменшае значэнне , пры якім выконваецца гэта роўнасць, атрымліваецца пры
:
Адкуль шуканы прамежак часу:
б) Прамежак часу , неабходны для праходжання першай паловы гэтай адлегласці
, вызначаецца з ураўнення:
Адкуль:
в) Прамежак часу , неабходны для праходжання другой паловы гэтай адлегласці, вызначаецца з суцадносіны:
Адказ: а) , б)
, в)
. Такім чынам, для праходжання першай паловы адлегласці цела затрачвае ў 2 разы менш часу, чым для праходжання другой паловы.
Практыкаванне 1-1
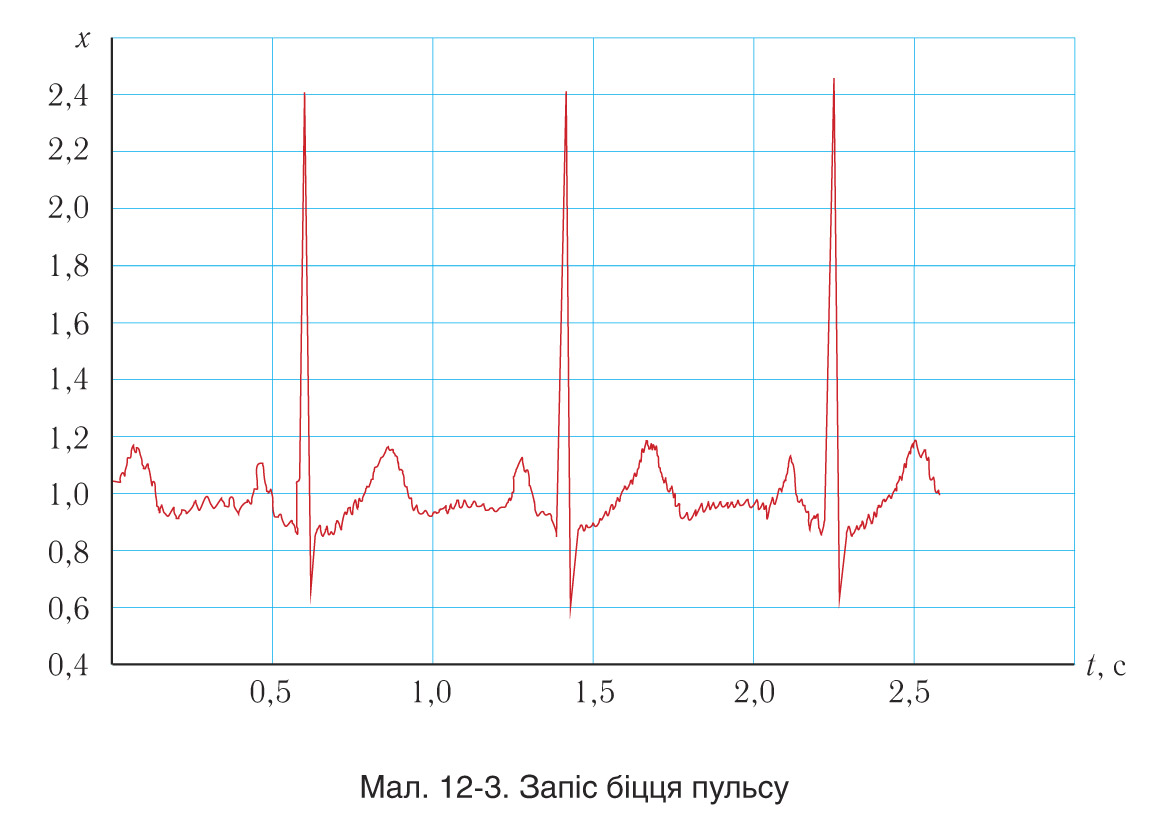
1. Вызначыце частату пульсу па асцылаграме, паказанай на малюнку 12-3.
2. Вызначыце найбольшыя значэнні модуляў скорасці і паскарэння
вагальнага матэрыяльнага пункта, калі амплітуда яго ваганняў А = 5,0 см, а перыяд ваганняў — Т = 3,0 с.
3. Матэрыяльны пункт выконвае ваганні па законе . За перыяд ваганняў Т пункт праходзіць шлях s = 40 см. Вызначыце каардынату
матэрыяльнага пункта ў момант часу
, калі фаза ваганняў
.
4. Амплітуда ваганняў матэрыяльнага пункта А = 1,0 см, частата Гц. Запішыце кінематычны закон руху
і пабудуйце графік залежнасці каардынаты пункта ад часу
. Вызначыце фазу
і каардынату пункта ў момант часу
, калі пачатковая фаза
.
5. Запішыце кінематычны закон руху матэрыяльнага пункта, калі за прамежак часу
ён выконвае
ваганняў з амплітудай
. У момант часу
пункт рухаўся ў напрамку восі Ох і яго каардыната х(0) = 5,0 см.