§ 28. Фотон. Уравнение Эйнштейна для фотоэффекта
| Сайт: | Профильное обучение |
| Курс: | Физика. 11 класс |
| Книга: | § 28. Фотон. Уравнение Эйнштейна для фотоэффекта |
| Напечатано:: | Гость |
| Дата: | Monday, 20 October 2025, 07:47 |
|
Изучение законов фотоэффекта привело ученых к неожиданному выводу: при взаимодействии с веществом (поглощении или излучении) свет ведет себя подобно движущимся частицам (квантам). Что это за частицы? Каковы их свойства и как они связаны с волновыми характеристиками света? |
Электронвольт — энергия, которую приобретет частица с зарядом, равным элементарному, при перемещении между двумя точками с ускоряющей разностью потенциалов 1В ().
Развивая идеи Планка, Эйнштейн в
По гипотезе Эйнштейна, монохроматическое электромагнитное излучение частотой обладает не только волновыми свойствами, но и свойствами характерными для потока частиц. Каждая такая частица движется со скоростью света с и несет квант энергии
. Назвать эти частицы фотонами предложил в
Энергия фотона может быть выражена через длину волны λ:
|
|
(1) |
Из релятивистского определения импульса для фотона
следует, что модуль его импульса определяется выражениями:
| (1-1) |
Следовательно, для фотона:
Исключая скорость из релятивистских выражений импульса и энергии тела:
получаем соотношение:
| (1-2) |
Для фотона из формулы (1-2) находим, что масса фотона равна нулю (m = 0).
Масса фотона, движущегося со скоростью света в вакууме, равна нулю.
Таким образом, фотон — удивительная частица, которая обладает энергией E = hν, импульсом , но вследствие того, что скорость фотона всегда равна скорости света в вакууме, то масса равна нулю (m = 0). Такие частицы называют безмассовыми.
Фотон является элементарной частицей, только в отличие от других элементарных частиц он не имеет массы, а потому «обречен» всегда двигаться со скоростью распространения света.
Таким образом, фотон обладает следующими свойствами:
— существует только в движении;
— является безмассовой частицей (m = 0);
— электрически нейтрален (q = 0);
—скорость его движения равна скорости распространения света в вакууме во всех ИСО;
— его энергия пропорциональна частоте соответствующего электромагнитного излучения (E = hν);
— модуль импульса фотона равен отношению его энергии к модулю скорости движения ().
Рассмотрим объяснение экспериментальных законов фотоэффекта, предложенное Эйнштейном на основе квантовых представлений. При освещении электрода электромагнитным излучением (см. рис. 171) происходит взаимодействие фотонов с электронами вещества. Если энергия фотона E = hν достаточно велика, то какой-либо из электронов после поглощения фотона может получить энергию достаточную для того, чтобы покинуть облучаемый образец. Электроны, покинувшие образец, имеют некоторую скорость, поэтому даже при отсутствии напряжения между электродами сила фототока не равна нулю. Именно поэтому, вольтамперная характеристика фотоэффекта при напряжении, равном нулю, не проходит через нуль (см. рис. 172, в).
Для того чтобы покинуть вещество электрон должен совершить работу против сил взаимодействия электрона с атомами вещества. Таким образом, минимальная энергия необходимая для выбывания электрона с поверхности вещества, называется работой выхода и обозначается Авых(Авых > 0). Для металлов эта работа связана с преодолением сил взаимодействия электронов с положительно заряженными ионами кристаллической решетки, которые удерживают электрон в веществе. Работа выхода для металлов обычно составляет несколько электронвольт (см. табл 9).
Таблица 9. Фотоэлектрические характеристики некоторых веществ
|
Вещество |
|
|
λк, нм |
|
Цезий |
1,9 |
4,6 |
650 |
|
Калий |
2,2 |
5,3 |
560 |
|
Натрий |
2,3 |
5,6 |
540 |
|
Кальций |
2,7 |
6,5 |
460 |
|
Цинк |
3,7 |
8,9 |
340 |
|
Серебро |
4,3 |
10 |
260 |
|
Вольфрам |
4,5 |
11 |
280 |
|
Никель |
5,0 |
12 |
250 |
|
Платина |
5,3 |
13 |
230 |
Оставшаяся часть энергии поглощенного кванта составляет кинетическую энергию освободившегося электрона. Наибольшей кинетической энергией будут обладать те электроны, которые поглотят кванты света вблизи поверхности металла и вылетят из него, не успев потерять энергию при столкновениях с другими частицами в металле. На основе закона сохранения энергии можно записать следующее уравнение для фотоэлектрона:
|
|
(2) |
Это соотношение называют уравнением Эйнштейна для внешнего фотоэффекта.
Отметим, что — это максимальная кинетическая энергия электрона
, которой он может обладать, вылетев из вещества. Из-за различных потерь кинетическая энергия электрона будет меньше расчетного значения.
Если энергия фотонов очень велика (рентгеновское или -излучение) для кинетической энергии необходимо использовать релятивистское выражение:
,
так как скорости фотоэлектронов сравнимы со скоростью света
Используя уравнение Эйнштейна, можно объяснить экспериментальные законы фотоэффекта.
Объяснение первого закона фотоэффекта. Сила фототока насыщения пропорциональна общему числу фотоэлектронов, покидающих поверхность металла за единицу времени. Число таких фотоэлектронов, в свою очередь, пропорционально числу фотонов, падающих на поверхность за это же время. Именно пропорционально, а не равно, так как часть квантов света поглощается кристаллической решеткой, и их энергия переходит во внутреннюю энергию металла. Таким образом, увеличение интенсивности падающего света приводит к росту числа фотоэлектронов, покидающих поверхность металла.
Объяснение второго закона фотоэффекта. Фотоэлектрон вырывается из катода за счет действия одного кванта падающего излучения. Поэтому кинетическая энергия фотоэлектрона зависит не от полной энергии волны, а от энергии одного кванта, т.е. частоты . При увеличении частоты падающего света максимальная кинетическая энергия
фотоэлектронов возрастает линейно, как следует из уравнения Эйнштейна для фотоэффекта (3), согласно соотношению:
| (3) |
Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, «затрудняющее» вылет электронов, то сила тока уменьшится, так как теперь фотоэлектронам, кроме работы выхода, придется совершать дополнительную работу против сил электрического поля.
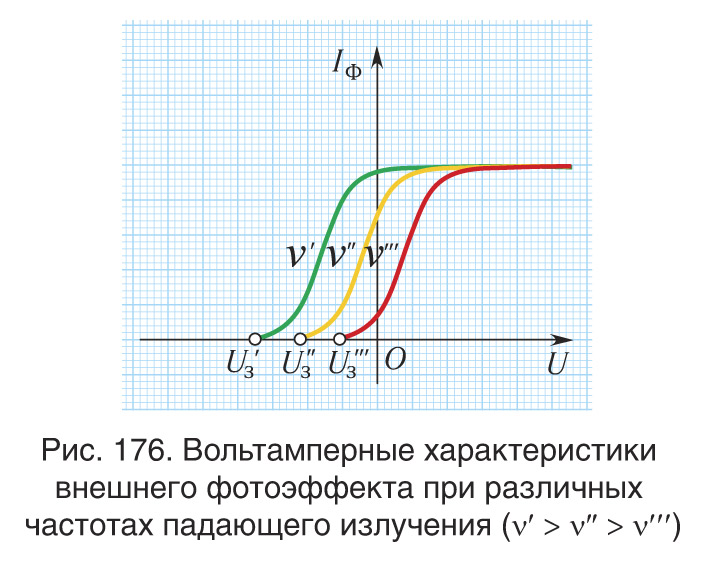
При некотором отрицательном значении напряжения Uз электроны затормаживаются и, не достигнув поверхности анода, возвращаются на катод. Сила тока в цепи при этом будет равна нулю (рис. 176). Величину Uз, при которой сила тока в цепи равна нулю, называют задерживающим напряжением. Следовательно, вся кинетическая энергия электронов затрачивается на работу против сил электрического поля. При этом максимальная кинетическая энергия электронов выражается через задерживающее напряжение следующим образом:
|
|
(4) |
Объяснение третьего закона фотоэффекта. Если частота ν падающего излучения меньше граничной частоты , при которой
, то испускания электронов не происходит
. Таким образом, фотоэффект отсутствует, если частота излучения оказывается меньше некоторой характерной для данного вещества величины
.
Следовательно, красную границу фотоэффекта можно найти из условия
|
|
(5) |
Она зависит только от работы выхода электронов, т.е. определяется строением металла и состоянием его поверхности.
Длина волны излучения, соответствующая красной границе фотоэффекта, может быть определена из соотношения
| (6) |
Из уравнения Эйнштейна для фотоэффекта (2) следует, что, находя тангенс tg α угла наклона прямых линий на рисунке 174, можно вычислить постоянную Планка, так как:
а по точкам пересечения продолжения графиков (см. рис. 175) с осями Uз и — найти работу выхода Авых и красную границу для данного вещества.
С появлением мощных монохроматических источников света (лазеров) удалось наблюдать процессы многофотонного поглощения. В таких процессах, прежде чем покинуть вещество, электрон может поглотить не один, а с несколько фотонов. Поэтому уравнение Эйнштейна для многофотонного фотоэффекта запишется в виде:
где N — число фотонов, за счет поглощения которых вылетел электрон.
Следовательно, для многофотонного фотоэффекта частота красной границы уменьшается в N раз, а соответствующая ей длина волны в N раз увеличивается:
В настоящее время трудно представить себе современную науку и технику без применения устройств (приемников излучения), преобразующих световые сигналы в электрические. Такие устройства называются фотоэлементами (рис. 177).
Фотоэлементы используются для контроля пассажиропотока в метро, для включения и выключения освещения на улицах, для управления производственными процессами, в военной технике: в самонаводящихся снарядах, для сигнализации и локации. Инфракрасные фотоэлементы широко используются в пультах дистанционного управления различными бытовыми электронными приборами (телевизор, кондиционер и т.д.).
|
В Первый фотоэлемент на внешнем фотоэффекте был создан Столетовым в 1888 г. |
 |
Вопросы к параграфу
- В чем сущность гипотезы Эйнштейна?
- Что называется фотоном? Перечислите основные свойства фотона.
- По какой формуле можно определить энергию фотона?
- Запишите уравнение Эйнштейна для фотоэффекта и назовите все физические величины, входящие в него.
- Покажите, что уравнение Эйнштейна для фотоэффекта является следствием закона сохранения и превращения энергии.
- Перечислите условия, необходимые для возникновения фотоэффекта.
- Что такое задерживающее напряжение?
- Что называется красной границей фотоэффекта? От чего она зависит?
- Как квантовая теория объясняет существование граничной частоты фотоэффекта? Запишите формулу для красной границы фотоэффекта.
- Объясните законы фотоэффекта исходя из квантовой теории света.
- Почему энергия фотоэлектронов для данного вещества определяется только частотой падающего света?
Примеры решения задач
1. Монохроматический свет длиной волны λ = 450нм падает на поверхность натрия. Определите: а) энергию E фотона этого света; б) модуль импульса p фотона падающего света; в) красную границу фотоэффекта для натрия; г) максимальную кинетическую энергию
фотоэлектронов.
Решение:
а) Энергия фотона:
,
.
б) Модуль импульса фотона:
.
в) Красная граница связана с работой выхода соотношением:
.
г) Из уравнения Эйнштейна для внешнего фотоэффекта находим, что максимальная кинетическая энергия вылетевшего электрона:
,
Ответ: а) , б)
, в)
, г)
.
2. Под действием света длиной волны с поверхности металла вылетают электроны, при этом их энергия равна половине энергии фотонов, вызывающих фотоэффект. Определите длину волны
, соответствующую красной границе фотоэффекта.
Решение:
Запишем уравнение Эйнштейна для фотоэффекта:
.
Красную границу фотоэффекта определим из соотношения:
.
По условию задачи:
Тогда , откуда следует, что
.
Так как длина волны , то
Ответ: λк=800нм.
Упражнение 19
1. Определите энергию E фотона для излучения частотой ν = 5,4 · 1014 Гц.
2. Вычислите энергию фотона видимого света длиной волны λ1 = 0,60 мкм и сравните ее с энергиями фотонов ультрафиолетового излучения длиной волны λ2= 0,252 мкм, рентгеновского излучения λ3= 0,10 мкм и γ - излучения λ4= 0,10 пм.
3. Определите красную границу νmin фотоэффекта для некоторого металла, если работа выхода электрона из него Авых = 3,3 · 10-19 Дж.
4. Определите длину волны λ ультрафиолетового излучения, падающего на поверхность цинка, при которой модуль максимальной скорости вылетающих фотоэлектронов составляет .

5. Определите работу выхода Авых электрона из катода, используя вольтамперную характеристику вакуумного фотоэлемента (рис. 178). Катод освещается светом с длиной волны λ=200 нм. Найдите число N электронов, выбиваемых из фотокатода в единицу времени.
6. Определите количество N фотонов с частотой ν = 9,5· 1012 Гц, которое содержится в импульсе излучения с энергией E = 8,8 · 10-18 Дж.
7. Определите максимальную кинетическую энергию и модуль максимальной скорости
фотоэлектрона, вылетевшего из натрия при облучении его ультрафиолетовым излучением длиной волны λ =200 нм.
8. На металлическую пластину падает монохроматический свет длиной волны λ = 413 нм. Определите работу выхода Авых (эВ) , если задерживающее напряжение U3 = 1,0 B.
9. Определите модуль импульса p фотона, соответствующего излучению длиной волны λ =600 нм.
10. Определите длину волны λ излучения, фотон которого имеет такую же энергию, как электрон, прошедший ускоряющую разность потенциалов Δφ = 4,1 В.
11. Определите максимальную скорость фотоэлектронов, вылетевших с поверхности цинка при освещении его ультрафиолетовым излучением длиной волны λ = 300 нм.
12. Определите работу выхода Авых электрона из вещества пластины, которую освещают светом с длиной волны λ = 350 нм, если наибольшее значение импульса, передаваемого пластине одним фотоэлектроном p = 3,0 · 10-25 кг · м/с.
13. Определите длину волны λ , если модуль импульса соответствующего этой волне фотона равен p = 1,3 · 10-27 кг · м/с .
14. Определите модуль импульса p фотона, вызывающего фотоэффект, если максимальная кинетическая энергия фотоэлектронов в k = 1,5 раза меньше работы выхода электронов из вещества катода Авых = 6,0 эВ.
15. Определите частоту ν νпадающих на поверхность металла фотонов, если максимальная энергия вылетевших фотоэлектронов Emax = 9,0 эВ , а работа выхода Авых = 2,7 эВ.
16. Фотон, которому соответствует длина волны λ = 4,0 · 10-10 м, претерпевает упругий центральный удар с покоившимся электроном и отлетает назад. Определите скорость электрона после соударения с фотоном.
17. Фотон, которому соответствует длина волны λ =4,0 · 10-10 м, сталкивается с покоившимся электроном и отлетает под углом к начальному направлению своего движения. Определите импульс
фотона после столкновения, считая скорость электрона после столкновения
.
18. Определите, на сколько Δt градусов нагреется капля воды объемом V = 0,70 мм3, если на нее ежесекундно падают N =2,5 · 1015 фотонов с длиной волны λ = 500 нм и полностью поглощаются каплей.
19. Определите длину волны λ электромагнитного излучения, которым облучают вольфрамовую пластинку, если известно, что фотоэлектроны с максимальной кинетической энергией проходят без отклонения область однородных взаимно перпендикулярных электрического и магнитного полей (рис. 178-1). Модуль напряженности электрического поля
, модуль индукции магнитного поля B =10 мТл.