§ 18-1. Формула сферического зеркала
| Сайт: | Профильное обучение |
| Курс: | Физика. 11 класс |
| Книга: | § 18-1. Формула сферического зеркала |
| Напечатано:: | Гость |
| Дата: | Thursday, 30 October 2025, 18:30 |
|
Сферические зеркала находят широкое применение в различных приборах и устройствах. Для их использования необходимо уметь рассчитывать их характеристики (положения изображений, их увеличения). Как же это можно сделать? |
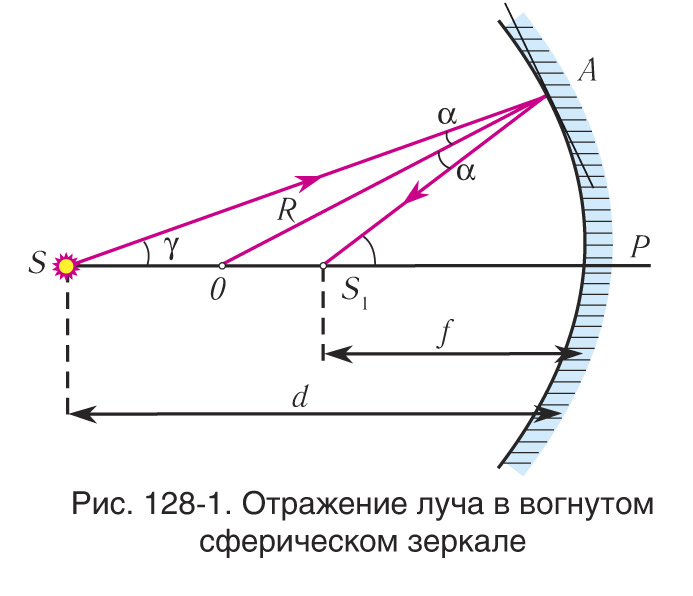
Получим формулу вогнутого сферического зеркала. Пусть точечный источник света S расположен на главной оптической оси за центром зеркала (рис. 128-1).
Расстояние SP от источника до зеркала обозначим SP = d . Луч SA после отражения пересечет ось в точке S1. Расстояние от зеркала до точки S1 обозначим S1P = f.
В ΔSAS1 линия AO является биссектрисой SAS1 и делит противоположную сторону на отрезки, пропорциональные двум другим сторонам треугольника:
Для луча SA, близкого к оптической оси
| (1) |
Кроме того, SO = d - R и OS1 = R - f.
Подставляя эти значения в пропорцию, получим
Это равенство приводится к виду (сделайте это сами):
Полученная формула называется формулой сферического зеркала.
Обратите внимание, что данная формула получилась при использовании приближенных равенств (1), т.е. она верна при падании на линзу параксиальных лучей.
Проанализируем полученную формулу. Если источник удалить от зеркала бесконечно далеко, то лучи, падающие на зеркало, будут идти параллельно оптической оси. Слагаемое станет равным нулю. Расстояние f будет равно некоторому значению F, и формула зеркала примет вид:
Откуда находим
Таким образом, лучи, параллельные главной оптической оси зеркала, отразившись от него, пересекаются в точке F, лежащей на главной оси и расположенной от полюса зеркала на расстоянии, равном половине его радиуса (см. рис. 114).
Это точка называется главным фокусом зеркала. Величина D, обратная фокусному расстоянию сферического зеркала, называется его оптической силой:
Единицей измерения оптической силы в СИ является диоптрия: 1 дптр = 1м-1.
Исходя из принципа обратимости лучей, можно сделать вывод, что лучи света от источника, помещенного в главный фокус зеркала, отразившись от него, пойдут параллельно главной оптической оси (см. рис. 147).
Расстояния d и R для любого луча, выходящего из точки S и падающего на зеркало, остаются неизменными. Поэтому луч после отражения будет пересекать ось в точке S1 . Таким образом, лучи, выходящие из какой-либо точки S на главной оси, расположенной за центром линзы, пересекаются после отражения от зеркала в одной и той же точке S1, также расположенной на этой оси. Эта точка S1 называется действительным изображением точки S .
Для действительных предмета, изображения и фокуса расстояния d, f и F считаются положительными, а для мнимых d, f и F — отрицательными.
Фокус выпуклого зеркала всегда мнимый, вогнутого — действительный.
Отметим, что при падении на зеркало расходящегося пучка, предмет будет действительным. При падении на зеркало сходящегося пучка, предмет будет мнимым.
Вогнутые зеркала используются для получения параллельных пучков света в различных отражателях или рефлекторах для освещения удаленных предметов (фары, прожекторы). Для этого следует поместить источник света в главном фокусе (рис. 128-2) вогнутого зеркала.
Полученное свойство фокусировки параллельного пучка лучей является приближенным и справедливым лишь для узкого пучка, т. е. лучей не слишком отстоящих от оптической оси. Для широких пучков имеет место сферическая аберрация, т.е. далекие от оптической оси лучи пересекают ее не в фокусе (см. рис. 128-2). Изображение при этом искажается — становится нерезким. Подобные искажения называются аберрациями оптических систем.
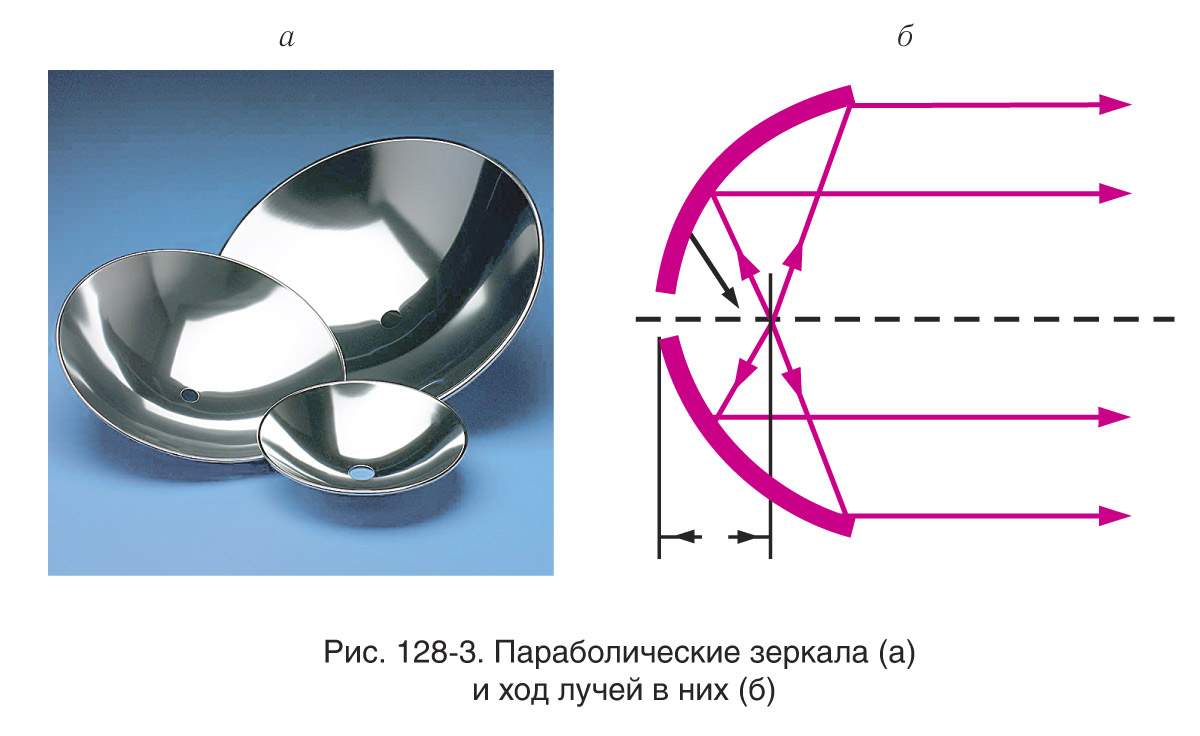
Сферическая аберрация — явление, при котором лучи, далеко отстоящие от главной оптической оси, соберутся не в форме зеркала, а в точке, расположенной на меньшем расстоянии от него. В результате точечный объект будет изображаться пятном. Для получения точечного осевого изображения зеркало должно быть параболическим (см. рис. 128-2, 128-3).
Такие зеркала используются во всех крупнейших телескопах. Но даже в них параллельные пучки, идущие под небольшими углами к оптической оси, после отражения не пересекаются в одной точке и дают сильно искаженные внеосевые изображения. Поэтому пригодное для работы поле зрения оказывается очень небольшим порядка нескольких десятков угловых минут.
Фокусное расстояние оказывается различным для лучей, находящихся на разных расстояниях от оптической оси (см. рис. 128-2). Однако для параксиального пучка (h << R) условие фокусировки выполняется и фокусное расстояние вогнутого зеркала оказывается равным F = R/2. В частности, при это выражение справедливо с относительной погрешностью не меньшей, чем 0,5 %.
Прожектор (от лат. projectus — брошенный вперед) — осветительный прибор с мощным источником света и вогнутым зеркалом, дающий пучок яркого света.
Вопросы к параграфу
- Получите формулу сферического зеркала.
- Что называется главным фокусом сферического зеркала? Оптической силой?
- Какое изображение получается в вогнутом зеркале, если предмет находится между полюсом и фокусом зеркала? Где оно находится?
- Какое изображение получается в выпуклом зеркале? Где оно находится?
- Где применяются очень большие вогнутые зеркала? Какая их основная функция?
- Может ли формироваться действительное изображение с выпуклым зеркалом?
- Как изменится действительное изображение предмета в вогнутом зеркале, если верхнюю половину зеркала прикрыть непрозрачным экраном?
- Чему равно фокусное расстояние любого плоского зеркала?
- Ограничивает ли дифракция изображения, создаваемые: а) сферическими зеркалами; б) плоскими зеркалами?
- Для чего используются параболические зеркала?
Пример решения задачи
1. Определите отношение величины изображения к величине предмета (увеличение), если главное фокусное расстояние вогнутого зеркала F , а расстояние от предмета до главного фокуса p.
F, p
Решение:
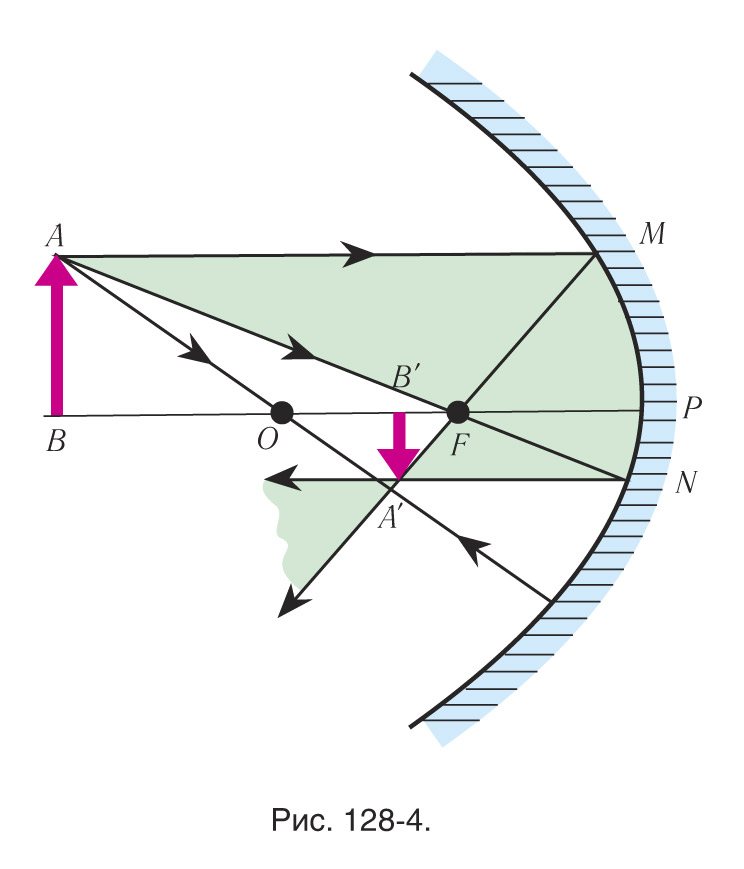
Из подобия ΔABF и ΔNFP (128-4) следует:
,
C учетом того, что d = p + F, то d - F = p.
Таким образом,
Ответ: .
2. В автомобиле выпуклое зеркало заднего вида имеет радиус кривизны R = 50 см. Определите положение f изображения и его увеличение Г, если наблюдаемый автомобиль находится на расстоянии d =12 м от зеркала.
R = 50 см = 0,5 0м
d = 12 м
Решение:
По формуле для выпуклого зеркала имеем:
.
Откуда:
.
Увеличение зеркала:
.
Таким образом, изображение в зеркале прямое и уменьшенное в 50 раз.
Ответ: f = 0, 24 м, Г = 0,02.
Упражнение 14-1
- Определите, где необходимо поместить
предмет перед вогнутым сферическим зеркалом, чтобы изображение совпало с предметом.
- Главное фокусное расстояние вогнутого сферического зеркала
. Определите расстояние
, на котором необходимо поместить предмет, чтобы его мнимое изображение получилось на расстоянии
.
- Вогнутое сферическое зеркало дает увеличенное в
раза перевернутое изображение предмета. Определите главное фокусное расстояние
зеркала и его радиус
, если предмет находится на расстоянии
от зеркала.
- Определите оптическую силу
выпуклого сферического зеркала, если расстояние до источника
, а от зеркала до изображения —
.
- Докажите, что увеличение
сферического зеркала, т. е. отношение некоторого линейного размера
изображения к соответствующему линейному размеру
предмета равно отношению расстояния
от изображения до зеркала к расстоянию
от предмета до зеркала:
.
- Предмет высотой
находится на расстоянии
перед вогнутым сферическом зеркалом с фокусным расстоянием
. Определите положение изображения
. Найдите высоту
изображения.
- Вогнутое сферическое зеркало имеет фокусное расстояние
. Где следует расположить предмет, чтобы мнимое изображение было в два раза дальше от зеркала?
- В выпуклом сферическом зеркале радиусом
получается уменьшенное в 5 раз изображение предмета. Определите расстояние
от предмета до зеркала.
- Докажите, что если
и
— расстояния от источника и его изображения до главного фокуса
сферического зеркала, то верна формула
.
- Покажите (см. рис. 113, б), что для
выражение для оптической силы сферического зеркала
имеет относительную погрешность
.
- Постройте график зависимости увеличения сферического зеркала от расстояния предмета до зеркала
.