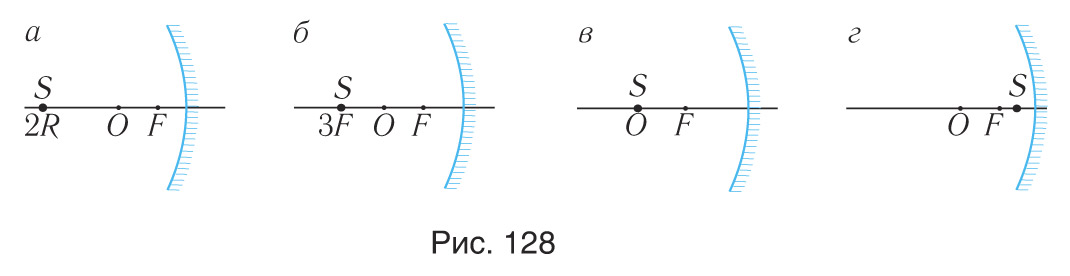§ 18. Вогнутые и выпуклые сферические зеркала. Построение изображений
| Сайт: | Профильное обучение |
| Курс: | Физика. 11 класс |
| Книга: | § 18. Вогнутые и выпуклые сферические зеркала. Построение изображений |
| Напечатано:: | Гость |
| Дата: | Воскресенье, 27 Июль 2025, 06:15 |
|
Каждое утро, умываясь, вы смотрите в плоское зеркало и видите свое четкое отражение в нем. Но поверхность зеркала может быть не только плоской, но и искривленной. Параллельные лучи света, отражаясь от искривленной поверхности, не останутся параллельными. Но отражаются они упорядоченно и могут как сходиться, так и расходиться (рис. 111). |
 Самый простой пример искривленной отражающей поверхности – сферическая поверхность. Зеркало с такой поверхностью называют сферическим.
Самый простой пример искривленной отражающей поверхности – сферическая поверхность. Зеркало с такой поверхностью называют сферическим.
Различают два типа сферических зеркал: вогнутые, если зеркальной является внутренняя поверхность сферы (рис. 112, а), и выпуклые, если — внешняя (рис. 112, б).
Основные характеристики сферических зеркал.
Рассмотрим основные характеристики сферических зеркал на примере вогнутого зеркала (рис. 113). Центр сферы O называется оптическим центром зеркала, его радиус R — радиусом зеркала. Вершина шарового сегмента P называется полюсом зеркала. Прямая линия OP, проходящая через оптический центр и полюс зеркала, называется главной оптической осью. Любая прямая, например прямая OM, проходящая через оптический центр O и поверхность зеркала (за исключением его главной оптической оси), называется побочной оптической осью.
Так как поверхность зеркала сферическая, то из ее геометрических свойств следует, что любая оптическая ось перпендикулярна поверхности зеркала. Поэтому луч, идущий по направлению к зеркалу по какой-либо из оптических осей, отразившись от зеркала, пойдет по той же самой оптической оси, но уже в обратном направлении.
 |
 |
В отличие от плоских зеркал, в которых изображение точечного источника всегда является точечным, в сферических зеркалах такое свойство выполняется только в случае, когда пучок падающих на зеркало лучей можно считать параксиальным (приосевым) (от греч. παρα — возле и лат. axis — ось). Это означает, что он состоит из лучей, образующих малые углы с оптической осью и находящихся на небольших расстояниях h по сравнению с радиусом кривизны R зеркала (h<<R).
В плоских зеркалах изображение точечного источника всегда является точечным. Сферические зеркала дают неискаженные изображения только в том случае, если предмет достаточно мал и лучи распространяются вблизи главной оптической оси.
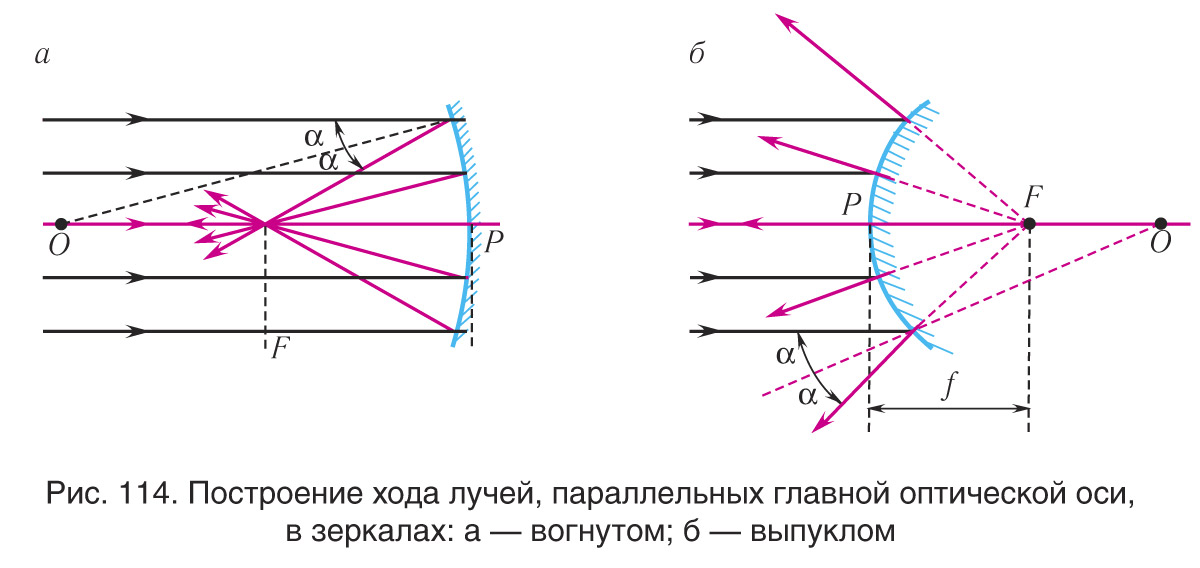
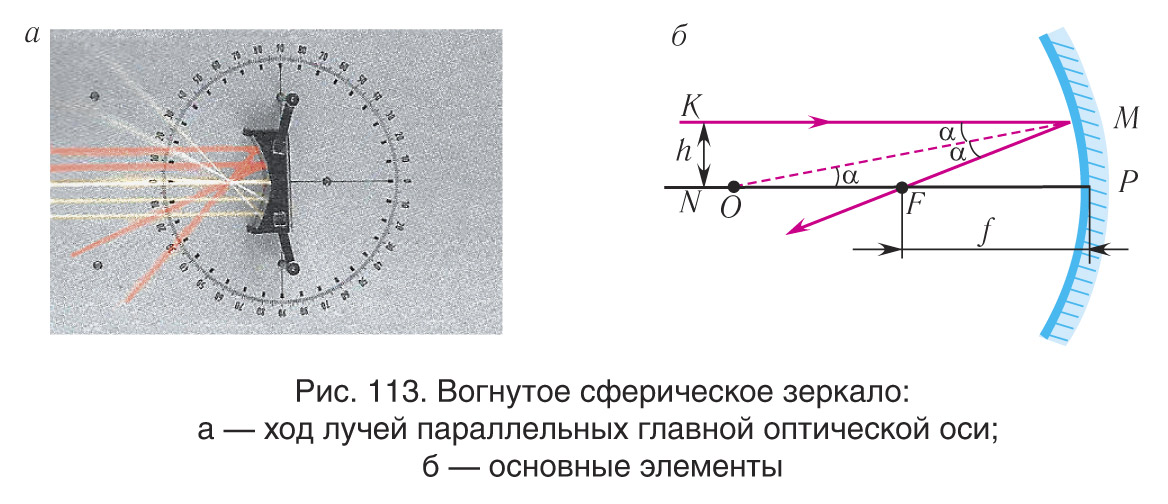
Если направить пучок лучей, параллельных главной оптической оси сферического зеркала, то все они пересекут главную оптическую ось в одной и той же точке (см. рис. 113, б). Рассмотрим луч KM, параллельный главной оптической оси OP (см. рис. 113, б). OM— нормаль к поверхности зеркала. Следовательно KMO=α, угол является углом падения. По закону отражения света луч, падающий на сферическое зеркало, и луч отраженный составляют с радиусом зеркала одинаковые углы α и лежат с ним в одной плоскости
KMO =
OMF. После отражения от зеркала луч пройдет через точку F на главной оптической оси (рис. 114, а). Так как треугольник ΔOMF равнобедренный, то OF=MF. Если расстояние h<<R, то FP≈MF. Следовательно, F≈PF≈FO=R/2.
Если направить пучок лучей параллельно главной оптической оси вогнутого сферического зеркала, то все они пересекут главную оптическую ось в одной и той же точке на расстоянии F=R/2 (рис. 113, 114, а). Аналогичные построения можно сделать и для выпуклого зеркала (рис. 114, б).
Только в отличие от вогнутого зеркала пересекаться в фокусе будут не лучи, а их продолжения. Эта точка находится на главной оптической оси на расстоянии от полюса зеркала — в мнимом фокусе.
Точка F (см. рис. 113, 114) называется главным фокусом зеркала. Расстояние PF = F от вершины зеркала до фокуса называется фокусным расстоянием. Фокусное расстояние зеркала равно половине радиуса его кривизны. Плоскость, проходящая через главный фокус F линзы перпендикулярно главной оптической оси, называется фокальной.
Из свойства обратимости оптических лучей следует, что луч, идущий от источника и проходящий через фокус F, после отражения пойдет параллельно главной оптической оси.
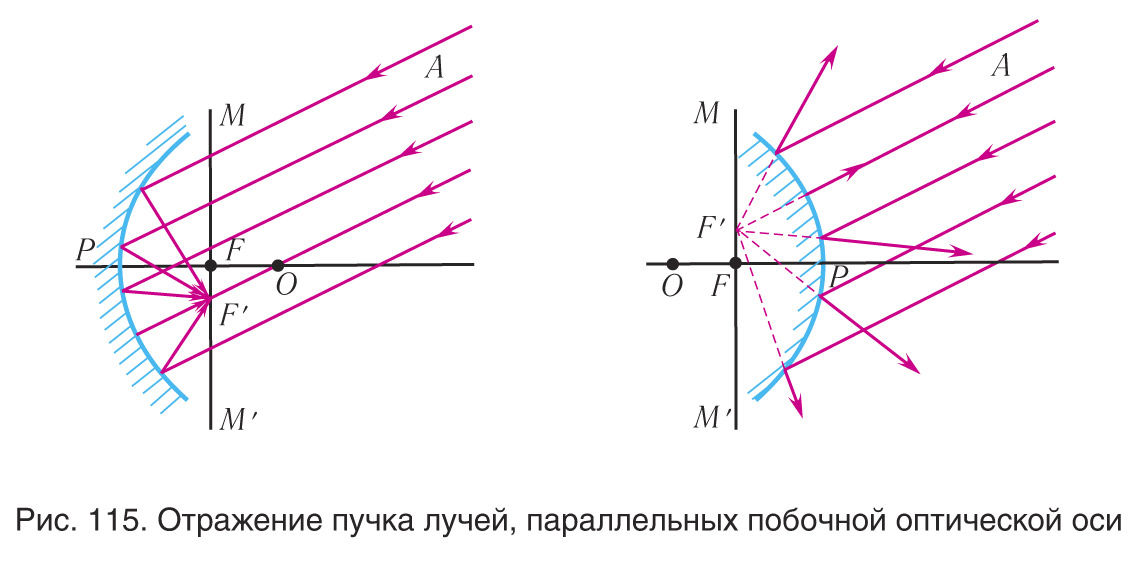
При падении пучка параллельных лучей под углом к главной оптической оси лучи после отражения пересекут побочную оптическую ось в точке называемой побочным фокусом F′ (рис. 115).
Построение изображений в сферических зеркалах
Для построения изображения любой точки в сферическом зеркале достаточно построить ход двух любых лучей в зеркале и найти их точку пересечения. Естественно, что для этого следует выбрать лучи, построить ход которых в зеркале проще всего.
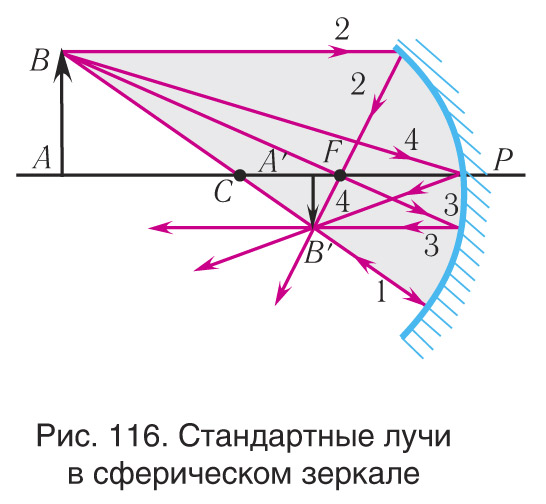
Как правило, для построений выбирают один из четырех стандартных (характерных) лучей (рис. 116):
- луч (1) — через центр зеркала — отраженный луч пойдет по тому же направлению в обратную сторону;
- луч (2) — параллельный главной оптической оси — отраженный луч проходит через главный фокус;
- луч (3) — через главный фокус — отраженный луч проходит параллельно главной оптической оси;
- луч (4) — падающий на зеркало в его полюсе — отраженный луч идет симметрично главной оптической оси.
Характеристики изображений
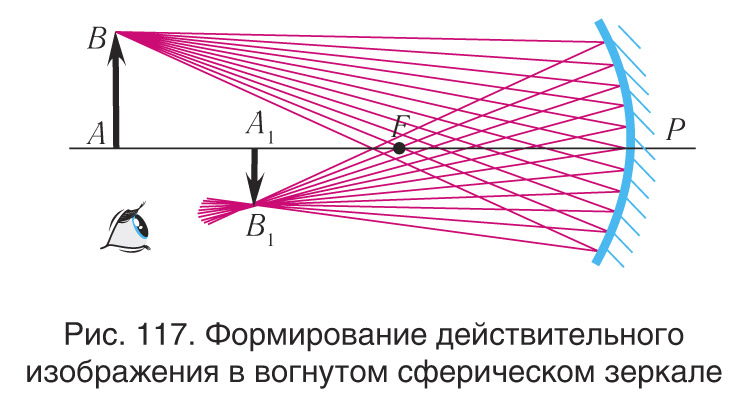
Если предмет AB (см. рис. 116, 117) перпендикулярен главной оптической оси в вогнутом сферическом зеркале, то его изображение будет также перпендикулярно этой оси. Поэтому достаточно построить изображение только точки B. Из свойств обратимости светового луча следует, что предмет AB и его изображение A1B1 можно поменять местами. Если предмет находится за оптическим центром зеркала, то изображение предмета — действительное, обратное и уменьшенное — находится между главным фокусом и центром зеркала (рис. 117).
Если предмет находится между фокусом и оптическим центром зеркала (см. рис. 117), то изображение A1B1 предмета — действительное, обратное и увеличенное — находится за центром зеркала.
 |
 |
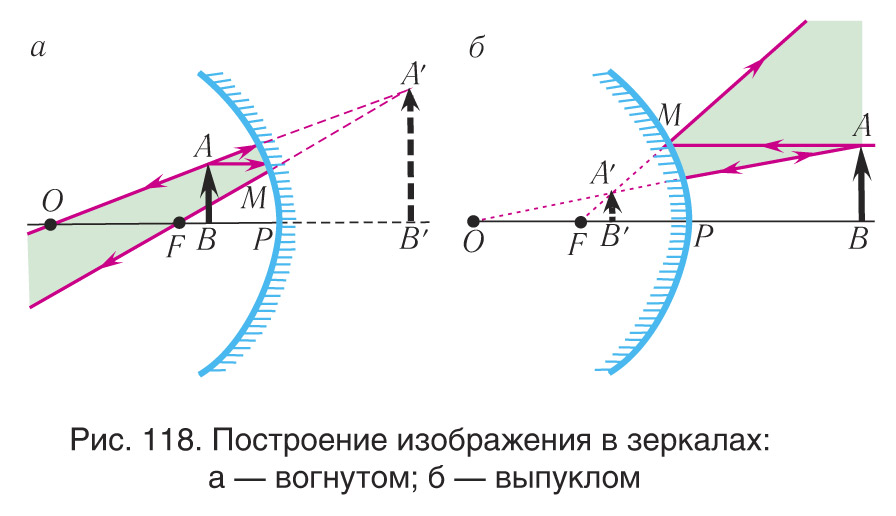
Если предмет находится между полюсом зеркала и его фокусом, то изображение A1B1 предмета — мнимое, прямое и увеличенное — находится за зеркалом (рис. 118, а).
Построим изображение предмета AB в выпуклом зеркале (рис. 118, б).
Изображение в таком зеркале всегда получается прямым, мнимым, уменьшенным.
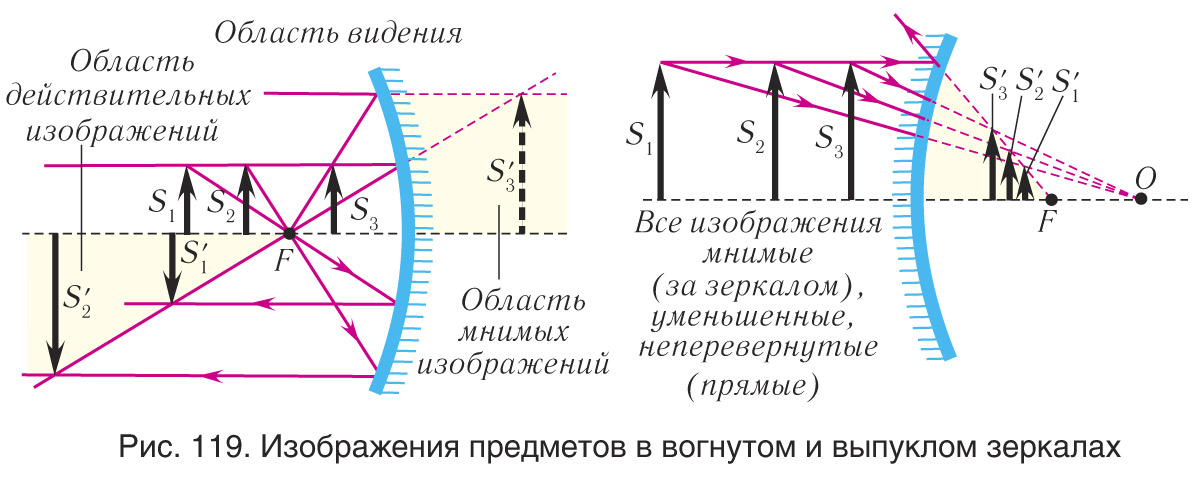
Все возможные изображения предметов в сферических зеркалах построены на рисунке 119.
Поскольку вогнутые зеркала фокусируют любое электромагнитное излучение, то они находят широкое применение в радиолокации, радиосвязи, радиоастрономии, в телевидении. В частности, вогнутые зеркала применяют в телескопах — приборах для наблюдения звезд, галактик.
|
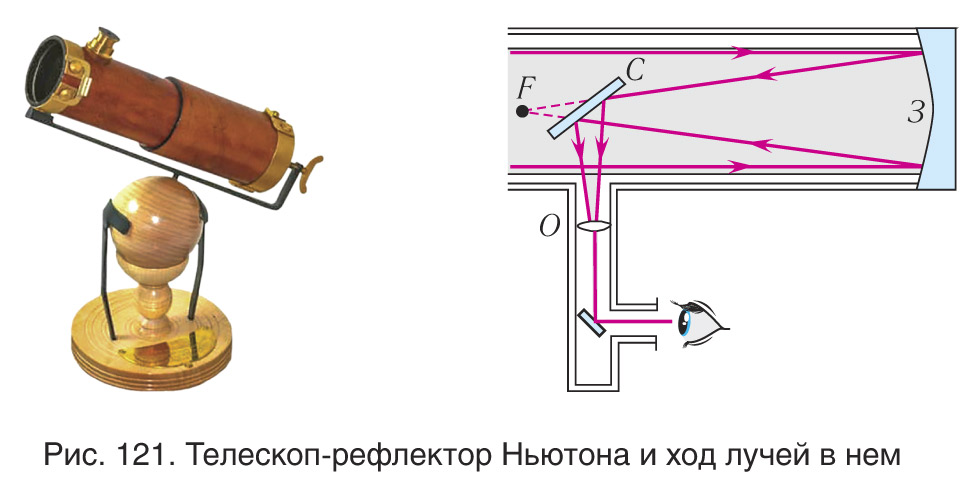
Чертеж первого прожектора был составлен Леонардо да Винчи в Атлантическом кодексе. Первый прожектор был построен в 1779 г. русским механиком И.П. Кулибиным. В настоящее время широко применяются светодиодные прожекторы (рис. 120). Они имеют рекордно низкое потребление электроэнергии, большой ресурс работ, небольшой вес, большую компактность и могут работать в широком температурном диапазоне Первый зеркальный телескоп-рефлектор был построен в 1668 г. И. Ньютоном (рис. 121). Современные телескопы-рефлекторы имеют зеркала большого диаметра. Так диаметр главного зеркала телескопа Маунт-Паломарской обсерватории в США — 5 м, а диаметр телескопа специальной обсерватории на Северном Кавказе в России — 6 м. |
|
|
|
 |
Вопросы к параграфу
- Дайте определение сферических зеркал и их классификацию.
- Дайте определения основных элементов сферических зеркал.
- Что называется главным фокусом зеркала? Фокальной плоскостью?
- Какие лучи используются для построения в сферических зеркалах?
- Что такое побочная оптическая ось и побочный фокус?
- Какие изображения получаются в сферических зеркалах: а) вогнутых; б) выпуклых?
Пример решения задачи
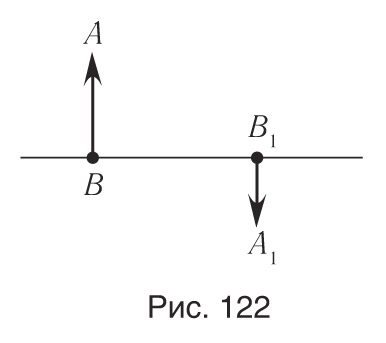
С помощью сферического зеркала получено изображение A1B1 предмета AB (рис. 122). Определите построением положение и фокус зеркала. Установите также тип зеркала (вогнутое или выпуклое). Известно, что ВВ1 — оптическая ось зеркала.
Решение
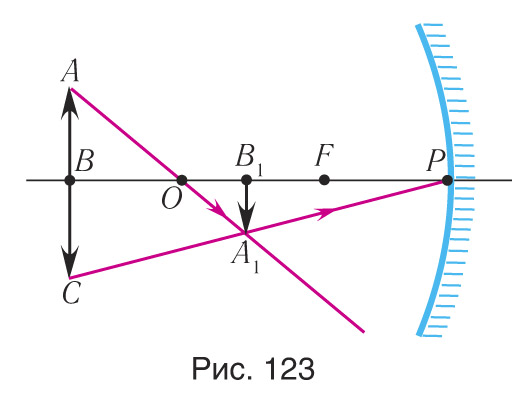
Как видно из рисунка 123, изображение A1B1 предмета AB является обратным и действительным. Следовательно, зеркало является вогнутым, поскольку только вогнутое зеркало дает действительное изображение. Соединим прямой линией точки A и А1. Точка O пересечения прямых и является центром кривизны сферического зеркала. Отразим точку A симметрично относительно оси в точку C. Проведем прямую СА1 до пересечения с прямой ВВ1. Точка Р пересечения будет полюсом вогнутого сферического зеркала. Разделив отрезок OP пополам, найдем положение фокуса F вогнутого зеркала.
Ответ: зеркало является вогнутым.
Упражнение 14
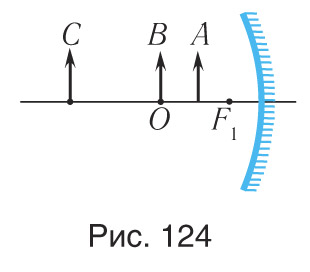
1. Постройте изображения предметов в вогнутых сферических зеркалах (рис. 124).
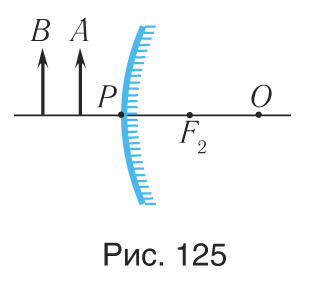
2. Постройте изображения предметов в выпуклых сферических зеркалах (рис. 125).
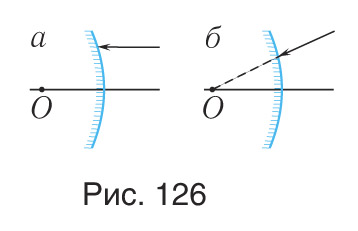
3. Постройте ход лучей в вогнутых сферических зеркалах (рис. 126).
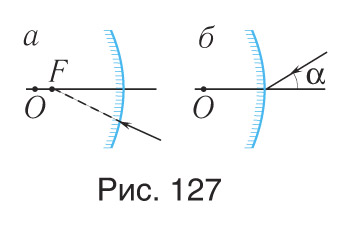
4. Постройте ход лучей в выпуклых сферических зеркалах (рис. 127).
5. Постройте изображение точечного источника света, находящегося в точке S (рис. 128).