§ 15. Интерференция света
| Сайт: | Профильное обучение |
| Курс: | Физика. 11 класс |
| Книга: | § 15. Интерференция света |
| Напечатано:: | Гость |
| Дата: | Вторник, 3 Июнь 2025, 07:10 |
|
Импульс тела можно скомпенсировать импульсом, имеющим противоположное направление. А можно ли погасить свет светом? При каких условиях два световых пучка при наложении друг на друга образуют темные и светлые полосы? Как осуществить такой эксперимент? |
Принцип суперпозиции электрических полей: напряженность электрического поля системы точечных зарядов q1,q2, ..., qn в некоторой точке пространства равна векторной сумме напряженностей полей, создаваемых в этой точке каждым из этих зарядов по отдельности, причем поле каждого не зависит от полей других:
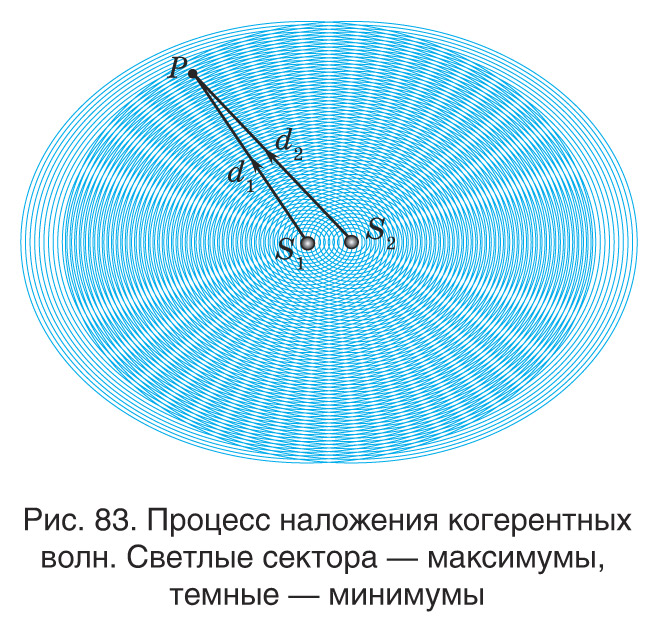
Рассмотрим процесс наложения световых волн длиной λ, возбуждаемых точечными источниками света S1 и S2 (рис. 83). В той области, где эти волны встречаются, происходит их наложение.
Так как световые волны имеют электромагнитную природу, для них так же, как и для электрических и магнитных полей, выполняется принцип суперпозиции (от лат. superposition — добавление). Согласно этому принципу колебания, вызванные волнами, складываются таким образом, что результирующее электромагнитное поле равно векторной сумме полей, созданных каждой из них: . При этом каждая из волн распространяется независимо от другой. В области, где волны перекрываются, возникает достаточно сложная картина (см. рис. 84). Однако, выйдя из этой области, волны распространяются так, как будто они свободно «проходят друг сквозь друга» и при этом никак не взаимодействуют между собой.
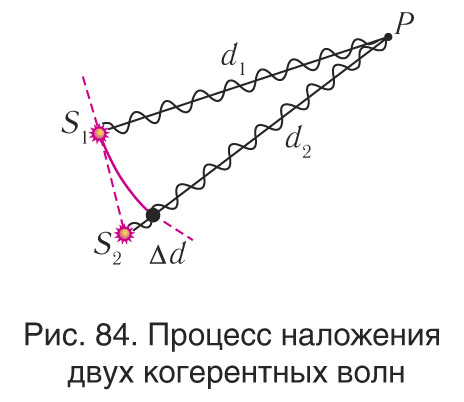
Если в точку P от монохроматических источников частотой ω пришли две волны, прошедшие разные расстояния d1 и d2 (рис. 84), то разность расстояний Δd = d2 − d1 называют разностью хода. Поскольку при разности хода Δd = λ разность фаз Δφ = 2π, то можно составить пропорцию . Из этого соотношения находим:
| (1) |
Следовательно, разность фаз Δφ определяется разностью хода Δd.
Волны одинаковых частот, разность фаз колебаний которых в каждой точке пространства не изменяется с течением времени, называются когерентными (когерентность от латинского слова cohaerens — связанный, сцепленный). Соответственно, свойство, характеризующее согласованность протекания в пространстве и времени нескольких колебательных или волновых процессов, называется когерентностью.
Предположим, что приходящие волны будут иметь в точке P напряженности электрического поля:
| (2) |
где E01, E02—амплитуды, α1, α2— начальные фазы колебаний каждой из волн в точке P.
Напряженность результирующего электрического поля согласно принципу суперпозиции в данной точке в любой момент времени равна векторной сумме напряженностей каждой волны по отдельности:
| (3) |
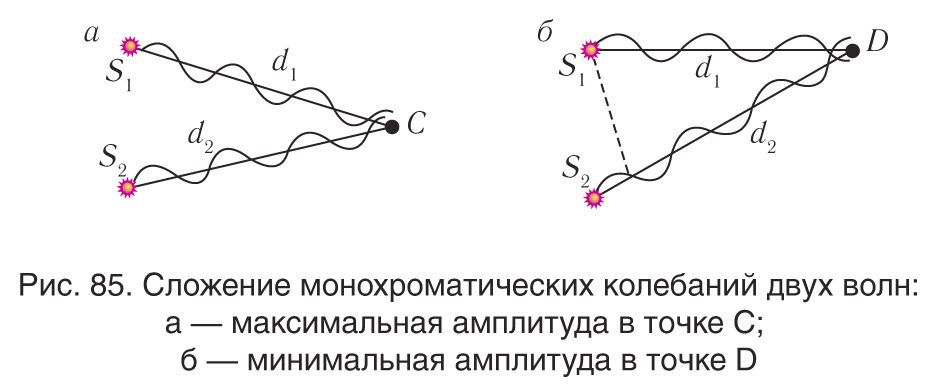
Если разность хода волн от источников S1 и S2 и кратна длине волны Δd = mλ, (m = 0, 1, 2, ...), то , и колебания, возбуждаемые волнами в точке C (рис. 85, а), происходят в одинаковой фазе. При этом гребень одной волны накладывается на гребень другой.
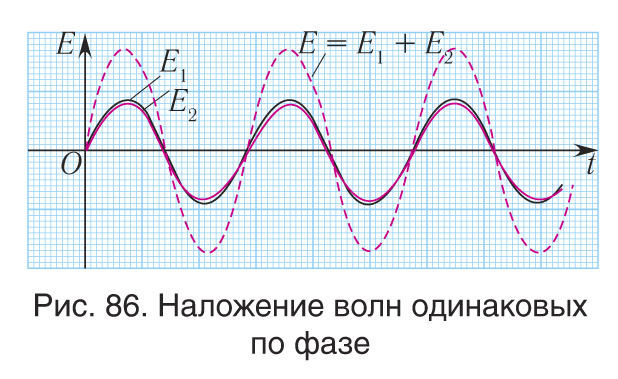
Соответственно, амплитуда результирующего колебания в точке C равна сумме амплитуд накладывающихся волн и оказывается максимальной (рис. 86)
| (4) |
Если же разность хода волн в точке D (рис. 85, б) равна нечетному числу полуволн , (m=0, 1, 2, ...), то
, и колебания происходят в противофазе. При этом гребень одной волны накладывается на впадину другой.
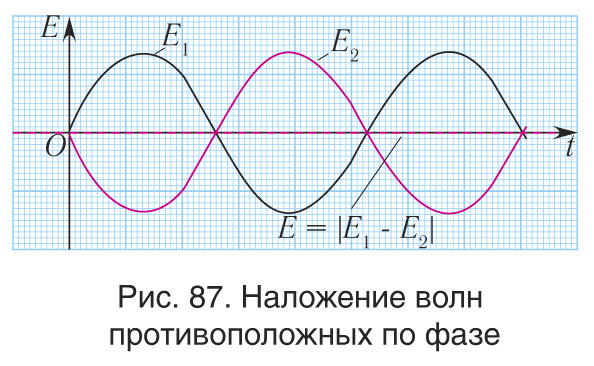
Таким образом, в этом случае амплитуда результирующего колебания равна модулю разности амплитуд накладывающихся волн и оказывается минимальной (рис. 87):
| (5) |
Заметим, что во всех других точках амплитуда А результирующего колебания имеет промежуточное значение:
Приемники излучения фиксируют не саму световую волну, а энергию, принесенную волной в данную область пространства. Параметром, характеризующим эту энергию, является интенсивность световой волны, которая обозначается латинской буквой I.
Согласно теории электромагнетизма интенсивность электромагнитной волны прямо пропорциональна квадрату амплитуды вектора напряженности ее электрического поля Символ
означает усреднение по времени. Аналогичное усреднение можно сделать и для вектора индукции магнитного поля
Исходя из соотношений (4) и (5), видно, что
т. е. интенсивность результирующей волны не равна сумме интенсивностей исходных волн. Это означает, что волны интерферируют друг с другом.
Вследствие зависимости разности фаз (1) от точки наблюдения, в пространстве получается сложная картина распределения интенсивности результирующей волны. Устойчивое во времени распределение амплитуд колебаний в пространстве при интерференции называется интерференционной картиной.
Таким образом, интерференция (от лат. inter — взаимно, между собой и ferio — ударяю, поражаю) — явление возникновения устойчивой во времени картины чередующихся максимумов и
минимумов амплитуд результирующей волны при сложении двух (или нескольких) когерентных волн.
Подчеркнем, что закономерности интерференции справедливы для волн любой природы (рис. 88) (электромагнитных, звуковых, волн на поверхности воды и т. д.), т. е. носят универсальный характер.
При рассмотрении интерференции света (электромагнитных волн) следует учесть, что длина волны света в веществе изменяется в зависимости от показателя преломления вещества. Если одна волна распространяется в веществе с показателем преломления n1, а другая — с показателем преломления n2, то разность фаз колебаний:
где:
| (7) |
Здесь δ — оптическая разность хода волн от источников до точки наблюдения, а величина nd — оптическая длина пути. Эта величина определяется расстояниями d1 и d2, пройденными световыми волнами с учетом их различных модулей скоростей v2 и v1 распространения в этих средах с показателями преломления n1 и n2.
Таким образом, если оптическая разность хода (7) равна целому числу длин волн в вакууме, то условие максимума интерференции:
|
|
(8) |
Волны приходят в точку P (см. рис. 85) синфазно, поскольку разность фаз в этом случае кратна 2π: .
Если оптическая разность хода (7) равна нечетному числу полуволн, то условие минимума интерференции:
|
|
(9) |
Волны приходят в точку P в противофазе и разность фаз колебаний в этом случае равна:
Для наблюдения интерференции света необходимы когерентные источники, излучающие волны с постоянной во времени разностью фаз. Распространенные обычные источники света (лампы накаливания, лампы дневного света, свечи и т. д.) не являются когерентными. Для того чтобы можно было наблюдать от них интерференцию света, свет от одного и того же источника необходимо разделить на два пучка и затем свести их вместе.

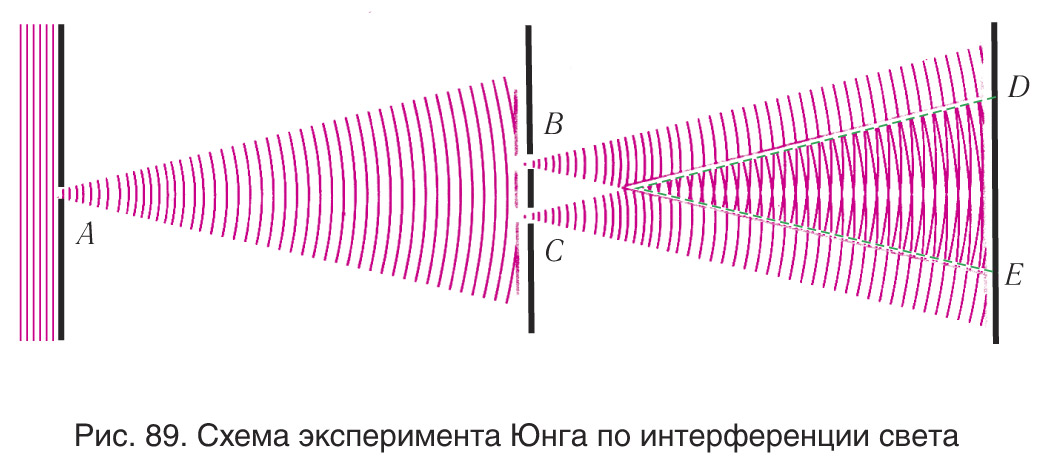
Для получения интерференционной картины пользуются классической интерференционной схемой (схемой Юнга), где пучок света от небольшого отверстия A в экране разделяется на два когерентных пучка с помощью небольших отверстий B и C в следующем экране (рис. 89). Поскольку эти пучки созданы одним и тем же источником A, они являются когерентными. Поэтому на третьем экране в области DE перекрытия пучков наблюдается интерференционная картина.
Изобретение и распространение когерентных источников излучения — лазеров — сделало демонстрацию явления интерференции достаточно простой.
Наиболее известное проявление интерференции, с которым мы часто встречаемся в повседневной жизни — радужное окрашивание мыльных пузырей (рис. 90) или тонких пленок, бензина (нефти) на воде или асфальте. Радужные цвета возникают на этих пленках вследствие интерференции света, отраженного двумя поверхностями пленки.
|
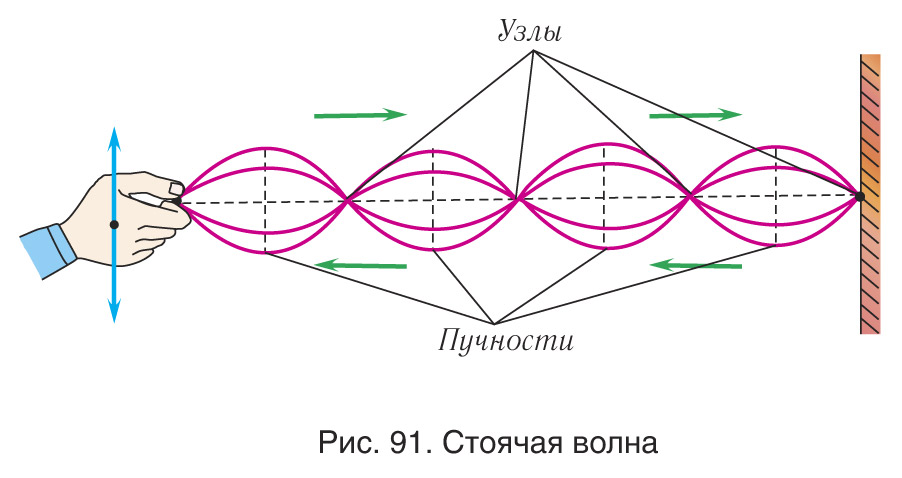
Английский ученый Томас Юнг в 1801 г. провел классический эксперимент по интерференции света (см. рис. 89). Это позволило ему убедительно подтвердить волновую природу света и длину световой волны. Отметим еще один распространенный случай интерференции - сложение волн одинаковой частоты, распространявшихся в противоположных направлениях (например, падающей и отраженной волны), приводящие к образованию в пространстве устойчивой картины чередования максимумов амплитуды колебаний — «пучностей» и минимумов — «узлов» (рис. 91). Волна, возникающая в результате сложения двух волн одинаковой частоты, распространяющихся в противоположных направлениях, называется стоячей волной. |
 |
Вопросы к параграфу
- Что такое когерентность? Какие волны называются когерентными?
- Что называют интерференцией волн? При каких условиях происходит это явление?
- Что называют разностью хода волн? Оптической разностью хода волн?
- Запишите условия образования интерференционных максимумов и минимумов. Какой должна быть оптическая разность хода двух волн, чтобы их интерференция приводила к ослаблению (усилению) результирующего сигнала?
- Почему не возникает интерференционной картины от света двух фар автомашины?
- Если две волны интерферируют друг с другом, то влияет ли одна волна на распространение другой?
- Почему мыльный пузырь на солнце играет всеми цветами радуги?
- Почему в тонком слое бензина, плавающем на поверхности воды, возникают радужные полосы?
- Почему интерференционная окраска одного и того же места поверхности мыльного пузыря непрерывно изменяется?
- При интерференции двух волн влияет ли одна волна на направление распространения другой?
Пример решения задачи
Определите положения максимумов и минимумов интерференционной картины на экране, находящемся на расстоянии L = AO = 2,0 м от двух одинаковых когерентных источников света S1 и S2 , которые расположены в вакууме на расстоянии d = 5,0 мм друг от друга (рис. 92). Длина волны излучения источников λ = 600 нм. Найдите расстояние Δx между соседними максимумами.
L = 2,0 м,
λ = 600 нм =6,00·10-7 м.
Решение:
До некоторой точки P на экране каждая из волн проходит различный путь l1 и l2. Максимумы и минимумы будут наблюдаться при выполнении условий соответственно
δ = l2 - l1 = mλ,
|
|
Из треугольников S1PA1 и S2PA2, по теореме Пифагора находим:
| (1) | ||
| (2) |
где xm — координата точки P.
Откуда, вычитая из соотношения (2) соотношение (1), получаем:
С учетом того что d << L и l1 + l2 2L находим:
|
|
Из условия максимумов следует:
| |
Тогда расстояние от центра экрана до m-й светлой полосы находится из соотношения:
| |
Из условия для минимумов находим положение темных полос:
| |
Откуда:
| |
Расстояние между соседними максимумами:
|
|
Из полученной формулы видно, что расстояние Δx увеличивается при уменьшении расстояния d между когерентными источниками.
Ответ:
Упражнение 11
1. Что будет наблюдаться в некоторой точке пространства в результате интерференции двух когерентных волн длиной волны λ=400 нм, оптическая разность хода которых δ=2,25 мкм?
2. Сколько длин волн N монохроматического излучения частотой ν=800 МГц укладывается на отрезке длиной l=2,0 м?
3. Экран MN освещен когерентными монохроматическими источниками S1 и S2 (см. рис. 92), период колебаний которых T. Усиление или ослабление света будет наблюдаться в точке P, если от источника S2 свет в нее приходит позже на промежуток времени τ=2,5T, чем от источника S1?
4. Две когерентные волны, длины волн которых λ=404 нм, приходят в одну точку на экране. Что будет наблюдаться в этой точке (усиление или ослабление света), если оптическая разность хода равна δ=17,17 мкм?
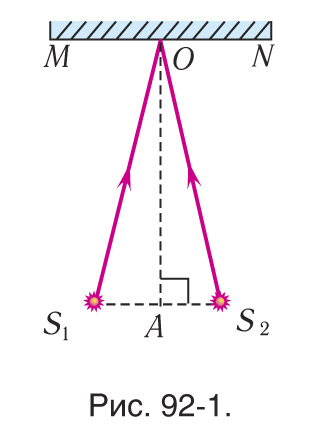
5. Два когерентных источника белого света S1 и S2 освещают экран MN, плоскость которого параллельна отрезку S1S2 (рис. 92-1). Докажите, что в точке O будет максимум освещенности, если S1O=S2O.
6. В установке Юнга расстояние между щелями d=1,5 см, экран расположен на расстоянии l=2,0 м от щелей. Щели освещаются монохроматическим источником, длина волны которого λ=687 нм. Определите расстояние Δx между интерференционными полосами на экране.
7. На экран A от точечного источника, находящегося от него на большом расстоянии, падает свет. В экране имеются две параллельные щели на расстоянии одна от другой. На экране B, расположенном на расстоянии l=1,0 м параллельно экрану A, расстояние между интерференционными полосами
. Определите длину волны λ излучения.