§ 7. Паняцце дапаможнага алгарытму

Сайт:	Профильное обучение
Курс:	Інфарматыка. 10 клас (Павышаны ўзровень)
Книга:	§ 7. Паняцце дапаможнага алгарытму
Напечатано::	Гость
Дата:	Суббота, 19 Апрель 2025, 15:36

7.1. Дапаможныя алгарытмы
7.2. Функцыі, якія вяртаюць лікавы вынік
7.3. Найбольшы агульны дзельнік двух лікаў
7.4. Функции, возвращающие логический результат
7.5. Функцыі, якія не вяртаюць вынік
7.6. Рэкурсія
Пытанні к параграфу
Практыкаванні

7.1. Дапаможныя алгарытмы

Дапаможны алгарытм — алгарытм, які можна выкарыстоўваць у іншых алгарытмах, назваўшы яго імя і, калі неабходна, значэнні параметраў. Дапаможны алгарытм, запісаны на мове праграміравання, называюць падпраграмай.

Асноўныя перавагі выкарыстання падпраграм:

1. Разбіццё комплекснай праграмнай задачы на простыя крокі (дэкампазіцыя). Гэта дазваляе размеркаваць рашэнне адной задачы паміж рознымі людзьмі.
2. Памяншэнне кода, які паўтараецца.
3. Шматразовае выкарыстанне кода ў іншых праграмах, у тым ліку і іншымі праграмістамі.
4. Утойванне дэталей рэалізацыі ад карыстальнікаў падпраграмы.

Падпраграмы, якія выкарыстоўваюцца часта, аб’ядноўваюць у бібліятэкі. Большасць моў праграміравання дазваляюць не толькі выкарыстоўваць гатовыя падпраграмы, але і пісаць свае. У мове C++ падпраграмы афармляюцца ў выглядзе функцый. Вам ужо даводзілася выкарыстоўваць розныя функцыі, напрыклад з бібліятэкі cmath.

Перад тым як выкарыстоўваць функцыю, яе трэба апісаць. Апісанне функцыі ўключае абвяшчэнне і вызначэнне функцыі.

Абвяшчэнне функцыі (прыклад 7.1) змяшчае ў сябе загаловак функцыі, які заканчваецца кропкай з коскай і ўключае:

імя функцыі f_N;
пералік фармальных параметраў
(type a_1, type a_2,… , type a_N);
тып значэння, якое вяртаецца
r_type:r _type f_N (type a_1, type a_2, ..., type a_N);

Функцыі могуць быць з параметрамі ці без параметраў. Калі функцыя не мае параметраў, то наяўнасць круглых дужак пасля імя функцыі абавязковая.

Вызначэнне функцыі складаецца з загалоўка функцыі (без кропкі з коскай) і цела функцыі, узятага ў фігурныя дужкі. У ім змяшчаюцца каманды мовы, якія рэалізуюць дапаможны алгарытм (прыклад 7.2).

Галоўная праграма на С++ таксама рэалізавана ў выглядзе функцыі. Гэта функцыя заўсёды мае імя main. Тып выніку і наяўнасць параметраў гэтай функцыі можа быць рознымі для розных асяроддзяў праграміравання. У асяроддзі Code::Blocks функцыя main() мае тып int і не мае параметраў.

Звычайна абвяшчэнне і апісанне падпраграм змяшчаюць да функцыі main(). Калі для рашэння задачы неабходна рэалізаваць некалькі функцый, то трэба памятаць пра тое, што функцыя павінна быць абвешчана да таго, як яна будзе выклікана.

Пры выкліканні функцыі (прыклад 7.3) паказваецца яе імя і параметры, неабходныя для вылічэнняў. Гэтыя параметры называюць фактычнымі параметрамі.

У апісанні функцыі задаецца спіс фармальных параметраў. Кожны параметр, апісаны ў гэтым спісе, з’яўляецца лакальным у адносінах да апісваемай функцыі, г. зн. на яго можна спасылацца па яго імені з дадзенай падпраграмы, але не з асноўнай праграмы ці іншай функцыі.

Пераменныя, значэнні якіх павінны быць вядомыя ва ўсіх функцыях, з’яўляюцца глабальнымі і апісваюцца да апісання функцый. Калі пераменная апісана паміж апісаннямі функцый, то яе значэнне будзе глабальным для ўсіх функцый, апісаных ніжэй, але невядомым для функцый, апісаных вышэй.

Неабходнасць аптымізацыі праграм па аб’ёме займаемай памяці прывяла да з’яўлення падпраграм. Падпраграмы дазволілі не паўтараць у праграме ідэнтычныя блокі кода, а апісваць іх аднакратна і выклікаць па меры неабходнасці.

Выкарыстанне падпраграм дазваляе павялічыць надзейнасць кода праграмы. Падпраграмы звычайна маюць невялікі памер, таму знайсці і выправіць у іх памылкі прасцей, чым у вялікай праграме.

Выкарыстанне падпраграм гарантуе адносную аўтаномнасць мадыфікацыі праграмы: калі трэба штосьці змяніць у праграме, перарабляць прыйдзецца не ўсю праграму, а толькі некаторыя падпраграмы.

Прыклад 7.1. Абвяшчэнне функцый.

int kol_cifr (int n);
double plos_treug(double a, double h);

double pi();

Прыклад 7.2. Вызначэнне функцыі.

int kol_cifr (int n)

{

int k = 0;

while (n >0 ) {

n /= 10;

k++;

}

return k;

}

double plos_treug(double a, double h)

{

double s = a * h / 2;

return s;

}

double pi()

{

return acos(-1.);

}

У асяроддзі Dev-C++ функцыя main можа мець аргументы:

У асяроддзі Microsoft Visual Studio тып значэння, якое вяртаецца, у функцыі main можа быць void:

Прыклад 7.3. Вызов функции.

int k = kol_cifr (12345);

double s_kv = 2 * plos_treug(a1, h1);

cout << pi();

У С++ абвяшчэнне і вызначэнне функцыі можа быць у розных месцах. Абвяшчэнне змяшчаюць да функцыі main, а вызначэнне пасля яе.

#include <iostream>

#include <cmath>

using namespace std;

int kol_cifr (int n);

double plos_treug(double a, double h);

double pi();

int main()

{

int k = kol_cifr (12345);

double a1 = 5, h1 = 3.2;

double s_kv = 2 * plos_treug(a1, h1);

cout << pi() << endl;

///...

return 0;

}

int kol_cifr (int n)

{

int k = 0;

while (n >0 ) {

n /= 10;

k++;

}

return k;

}

double plos_treug(double a, double h)

{

double s = a * h / 2;

return s;

}

double pi()

{

return acos(-1.);

}

7.2. Функцыі, якія вяртаюць лікавы вынік

Большасць функцый з бібліятэкі cmath, якія выкарыстоўваліся раней, вяртаюць у якасці выніку лік.

Для таго каб функцыя магла вяртаць значэнне, выкарыстоўваецца аператар return. Пасля яго паказваецца значэнне, што вяртаецца. Гэтым значэннем можа быць канстанта (значэнне 0 у функцыі main), пераменная (у прыкладзе 7.2 гэта функцыі plos_treug і kol_cifr) або выраз (функцыя pi() у прыкладзе 7.2).

Тып значэння, якое вяртаецца, павінен супадаць з тыпам выніку ў апісанні функцыі [1].

Прыклад 7.4. Для функцыі $begin mathsize 16px style f left parenthesis x right parenthesis space equals space fraction numerator square root of open vertical bar x space minus space 2 close vertical bar end root over denominator x squared space plus space 3 end fraction end style$ вылічыць і вывесці: $f open parentheses – 2.4 close parentheses comma space space f left parenthesis y right parenthesis comma space space f left parenthesis f left parenthesis 3.7 space asterisk times space z right parenthesis right parenthesis$ . Значэнні пераменных y і z уводзяцца.

Этапы выканання задання

I. даныя: лікі y, z.

II. Вынік: f1, f2, f3 — значэнні функцыі для названых значэнняў аргументаў.

III. Алгарытм рашэння задачы.

1. Увод зыходных даных.
2. Апішам функцыю, якая вылічвае значэнне f па паказанай формуле.
3. Вылічым значэнне функцыі для паказаных аргументаў.
4. Вывад значэнняў функцыі.

VI. Апісанне пераменных: y, z, f1, f2, f3 – double.

Разгледзім, як выконваецца праграма. Пры выкліку функцыі значэнне фактычнага параметра перадаецца фармальнаму і адбываецца вылічэнне з гэтым значэннем.

У першым выпадку фактычным параметрам з’яўляецца канстанта –2.4. Таму пераменная x атрымае значэнне –2.4, пераменная $t 1 space equals space square root of open vertical bar – 2.4 space – space 2 close vertical bar end root space almost equal to space 2.097 comma$ пераменная $t 2 space equals space x squared space plus space 3 space equals space 8.76.$ Функцыя верне значэнне $fraction numerator 2.097 over denominator 8.76 end fraction space almost equal to space 0.239 comma$ якое і будзе нададзена пераменнай f.

У другім выпадку пераменнай x будзе перададзена значэнне пераменнай y, якое ўвялі з клавіятуры, і затым будуць выкананы вылічэнні.

У трэцім выпадку выклік функцыі ажыццяўляецца двойчы: спачатку для значэння 3.7 * z, а затым аргументам функцыі стане значэнне f(3.7 * z).

Прыклад 7.5. Дазены тры лікі. Знайсці парныя здабыткі гэтых лікаў. Напісаць праграму, якая вылічыць мінімальнае і максімальнае з гэтых значэнняў.

Этапы выканання задання

I. Зходныя даныя: лікі x, y, z.

II. Вынік: minpr, maxpr (мінімальны і максімальны здабыткі).

III. Алгарытм рашэння задачы.

1. Увод зыходных даных.
2.Апішам функцыі, якія вылічваюць мінімальнае і максімальнае значэнне для двух лікаў.
3. Знаходзім парныя здабыткі лікаў x, y, z. Такіх здабыткаў будзе тры: xy, yz, xz.
4. Для знаходжання мінімальнага значэння з трох лікаў выкарыстаем наступную уласцівасць:
Min(a1, a2, a3) = Min(Min(a1, a2), a3). Максімальнае значэнне знаходзіцца аналагічна.
5. Вывад вынікаў.

IV.Апісанне пераменных: усе пераменныя ў праграме маюць тып int.

Прыклад 7.6. Выпуклы чатырохвугольнік зададзены каардынатамі сваіх вяршынь. Напісаць праграму, якая знойдзе перыметр і плошчу чатырохвугольніка. Вылічэнне даўжыні адрэзка і плошчы трохвугольніка аформіць у выглядзе падпраграм.

Этапы выканання задання

I. Зыходныя даныя: x1, y1, x2, y2, x3, y3, x4, y4 (каардынаты вяршынь).

II. Вынік: P і S — перыметр і плошча чатырохвугольніка.

III. Алгарытм рашэння задачы.

1. Увод зыходных даных.
2. Перыметр чатырохвугольніка — сума даўжынь яго старон. Даўжыня стараны — даўжыня адрэзка, які злучае вяршыні. Вылічэнне даўжыні адрэзка афармляем у выглядзе функцыі dlin.
3. Для вылічэння плошчы правядзём дыяганаль, якая злучае вяршыні з каардынатамі (x1, y1) і (x3, y3) або (x2, y2) и (x4, y4). Чатырохвугольнік разаб’ецца на два трохвугольнікі, сума плошчы якіх і дасць шуканую плошчу. Плошчу трохвугольніка вылічым па формуле Герона,паколькі для трохвугольнікаў вядомыя даўжыні старон. Абазначэнні дапаможных пераменных — на малюнку.

Вылічэнне плошчы трохвугольніка афармляем у выглядзе функцыі plos.
4. Вывад выніку.

IV. Апісанне пераменных: усе пераменныя ў праграме маюць тып double.

[1] Пры несупадзенні тыпаў адбываецца спроба пераўтварэння тыпаў. Калі г эта немагчыма, то кампілятар выдасць памылку.

Значэнне 0, якое вяртае функцыя main, гаворыць пра адсутнасць памылак пры выкананні праграмы. Гэта азначае, што ўсе каманды, якія знаходзяцца ў праграме да гэтага радка, выканаліся паспяхова. Каманда return 0; можа быць выкарыстана для перарывання работы функцыі. Ніякія каманды не могуць быць выкананы пасля яе.

Пра паспяховае выкананне праграмы сведчыць паведамленне «Process terminated with status 0» у акне Build log.

Калі работа праграмы была перапынена (напрыклад, карыстальнік закрыў кансольнае акно да таго, як праграма скончыла работу), то ў гэтым акне будзе паведамленне пра памылку: «Process terminated with status —1073741510»

Прыклад 7.4.

V. Праграма:

#include <iostream>

#include <cmath>

using namespace std;

double f(double x)

{

double t1 = sqrt(abs(x - 2));

double t2 = x * x + 3;

return t1 / t2;

}

int main()

{

double y, z;

cout << "vvedi 2 chisla" << endl;

cin >> y >> z;

double f1 = f(-2.4);

cout << "f1 = " << f1 << endl;

double f2 = f(y);

cout << "f2 = " << f2 << endl;

double f3 = f( f(3.7 * z) );

cout << "f3 = " << f3 << endl;

return 0;

}

VI. Тэсціраванне.

VII. Аналіз выніку. Праверыць правільнасць вылічэнняў можна з дапамогай калькулятара.

Прыклад 7.5.

V. Праграма:

#include <iostream>

using namespace std;

int Max(int c,int d)

{

if (c > d)

return c;

else

return d;

}

int Min(int c, int d)

{

if (c < d)

return c;

else

return d;

}

int main()

{

int x, y, z;

cout << "vvedi 3 chisla" << endl;

cin >> x >> y >> z;

int a1 = x * y;

int a2 = y * z;

int a3 = x * z;

int s = Min(a1, a2);

int minpr = Min(s, a3);

cout << "min proiz = " << minpr << endl;

s = Max(a1, a2);

int maxpr = Max(s, a3);

cout << "max proiz = " << maxpr << endl;

return 0;

}

VI. Тэсціраванне.

Прыклад 7.6.

V. Праграма:

#include <iostream>

#include <cmath>

using namespace std;

double dlin(double x, double y, double x0, double y0)

{

double d = (x - x0) * (x - x0) + (y - y0) * (y - y0);

return sqrt(d);

}

double plos(double a, double b, double c)

{

double pr = (a + b + c) / 2;

double pl = sqrt(pr * (pr - a) * (pr - b) * (pr - c));

return pl;

}

int main()

{

double x1,y1,x2,y2,x3,y3,x4,y4;

cout << "koordinaty vershiny 1 - ";

cin >> x1 >> y1;

cout << "koordinaty vershiny 2 - ";

cin >> x2 >> y2;

cout << "koordinaty vershiny 3 - ";

cin >> x3 >> y3;

cout << "koordinaty vershiny 4 - ";

cin >> x4 >> y4;

///стораны і дыяганаль

double a1 = dlin(x1, y1, x2, y2);

double a2 = dlin(x2, y2, x3, y3);

double a3 = dlin(x3, y3, x4, y4);

double a4 = dlin(x4, y4, x1, y1);

double d = dlin(x1, y1, x3, y3);

///перыметр

double p = a1 + a2 + a3 + a4;

///плошча

double s1 = plos(a1, a2, d);

double s2 = plos(a3, a4, d);

double s = s1 + s2;

cout << "perimetr=" << p << endl;

cout << "ploschad=" << s << endl;

return 0;

}

VI. Тэсціраванне.

VII. Аналіз выніку. Звярніце ўвагу на імёны пераменных у праграме. Фактычныя і фармальныя параметры прынята называць рознымі імёнамі.

7.3. Найбольшы агульны дзельнік двух лікаў

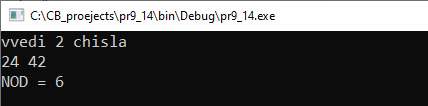
Найбольшым агульным дзельнікам (НАД) для двух цэлых лікаў называюць найбольшы з іх агульных дзельнікаў. Прыклад: для лікаў 42 і 24 найбольшы агульны дзельнік роўны 6.

Існуюць некалькі алгарытмаў знаходжання НАД. На ўроках матэматыкі вы пазнаёміліся з наступным алгарытмам:

1) раскласці кожны з лікаў на простыя множнікі;

2) выбраць у раскладаннях агульныя множнікі;

3) перамножыць выбраныя лікі;

(Разгледзім прыклад 7.7.)

На ўроках інфарматыкі ў 8-м класе вы пазнаёміліся з алгарытмам Эўкліда:

1) ад большага ліку аднімаем меншы;

2) калі атрымліваецца 0, то лікі роўныя адзін аднаму і гэта значэнне з’яўляецца НАД;

3) калі вынік адымання не роўны 0, то большы лік замяняем на рознасць большага і меншага;

4) пераходзім да пункта 1.

(Р азгледзім прыклад 7.8.)

Для рэалізацыі алгарытму з курса матэматыкі спатрэбіцца рэалізацыя некалькіх функцый: функцыя для раскладання ліку на множнікі, функцыя для параўнання двух раскладанняў і адбору аднолькавых лікаў, функцыя для перамнажэння лікаў. Акрамя таго, спатрэбіцца дадатковая памяць, каб захоўваць раскладанне лікаў. У той жа час для знаходжання НАД па алгарытме Эўкліда дастаткова адной функцыі, якая будзе працаваць з дзвюма перменнымі.

Прыклад 7.9. Напісаць праграму вылічэння НОД(a, b, c).

Этапы выканання задання

I. Зыходныя даныя: a, b і c (тры лікі).

II. Вынік: НОД (a, b, c).

III. Алгарытм рашэння задачы.

1. Увод лікаў a, b, c.
2. ВВыкарыстаем тое, што НАД (a, b, c)= НОД (НОД (a, b), c). Гэта значыць спачатку вылічым d = НОД (a, b), а затым f = НОД (d, c).
3. Для вылічэння НАД двух лікаў складзём функцыю gcd[1](x, y), якая вылічвае значэнне НАД двух лікаў па алгарытме Эўкліда.
4. Вывад выніку.

IV. Апісанне пераменных: a, b, c, d, f – int.

Прыклад 7.10. На плоскасці зададзены адрэзак, канцы якога маюць цэлалікавыя каардынаты. Колькі пунктаў з цэлалікавымі каардынатамі належаць гэтаму адрэзку? Напрыклад, для адрэзка з канцамі (–5; 5) і (4; –1) такіх пунктаў будзе 4.

Этапы выканання задання

I. Зыходныя данныя: x1, y1, x2, y2 (каардынаты канцаў адрэзка).

II. Вынік: k — колькасць навучэнцаў.

III. Алгарытм рашэння задачы.

1. Увод зыходных даных.
2. Пункты з цэлалікавымі каардынатамі падзеляць адрэзак на часткі. Колькасць такіх частак будзе роўна
$НОД space open parentheses open vertical bar x subscript 1 space minus space x subscript 2 close vertical bar comma space space open vertical bar y subscript 1 space minus space y subscript 2 close vertical bar close parentheses.$
3. Колькасць пунктаў на адну большая, чым колькасць частак.
4. Для вылічэння НАД двух лікаў саставім функцыю gcd(x, y), якая вылічвае значэнне НАД двух лікаў па алгарытме Эўкліда.
5. Вывад выніку.

IV. Апісанне пераменных: x1, y1, x2, y2, k – int.

Прыклад 7.11. Паралель дзясятых класаў напісала кантрольную работу. У выніку роўна a% навучэнцаў атрымалі адзнакі ад 7 да 10, астатнія — ад 1 да 6. Якая мінімальная колькасць навучэнцаў павінна быць у паралелі дзясятых класаў для таго, каб мог атрымацца такі вынік?

Этапы выканання задання

I. Зыходныя даныя: а — колькасць працэнтаў паспяховых работ.

II. Вынік: k — количество учащихся.

III. Алгарытм рашэння задачы.

1. Увод зыходных даных.
2. Калі а — колькасць працэнтаў работ, выкананых на 7—10, то колькасць працэнтаў астатніх работ:
b = 100 – а.
3. Мінімальная колькасць: $k space equals space fraction numerator 100 over denominator НОД left parenthesis straight а comma space straight b right parenthesis end fraction$ .
4.Для вылічэння НОД двух лікаў складзём функцыю gcd (x, y), якая вылічвае значэнне НАД двух лікаў па алгарытму Эўкліда.
5. Вывад выніку.

IV. Апісанне пераменных: a, b, k — int.

[1] gcd — от англ. greatest common divisor (найбольшы агульны дзельнік).

Пример 7.7. Знаходжанне найбольшага агульнага дзельніка для лікаў 42 і 24:

1) $begin mathsize 14px style 42 space equals space 2 space times space 3 space times space 7 comma space space space 24 space equals space 2 space times space 2 space times space 3 colon end style$

2) агульныя множнікі: 2 і 3;

3) $begin mathsize 14px style НОД space equals space 2 space times space 3 space equals space 6. end style$

Прыклад 7.8. Алгарытм Эўкліда для лікаў 42 і 24:

a	b
42	24
18 (42−24)	24
18	6 (24−18)
12 (18−6)	6
6 (12−6)	6

Аналізуючы дзеянні, якія выконваюцца ў алгарытме Эўкліда, можна заўважыць, што можна замяніць большы лік на астачу ад дзялення большага ліку на меншы. Карэктнасць дадзенага факту вынікае з наступнага сцверджання: калі a = b · q + r, то НОД(a, b) = НОД(b, r). Пры такой арганізацыі вылічэнняў алгарытм скончыць сваю работу, калі адзін з лікаў стане роўным нулю. Тады значэнне НАД будзе роўна іншаму ліку, паколькі НОД(r, 0) = r для любога ненулявога r (паколькі 0 дзеліцца на любы цэлы лік).

Прыклад 7.9.

V. Праграма:

#include <iostream>

using namespace std;

int gcd (int x, int y)

{

while (y != x){

if (x > y)

x -= y;

else

y -= x;

}

return x;

}

int main()

{

int a, b, c;

cout << "vvedi 3 chisla" << endl;

cin >> a >> b >> c;

int d = gcd(a, b);

int f = gcd(d, c);

cout << "NOD = " << f << endl;

return 0;

}

VI. Тэсціраванне.

Для кампілятара MinGW, які ўстанаўліваецца разам з Code::Bloks, рэалізавана функцыя __gcd(n, m). Яна знаходзіць НАД двух лікаў. Выкарыстоўваць гэту функцыю можна пасля падключэння бібліятэкі algorithm.

Прыклад 7.10.

V. Праграма:

#include <iostream>

#include <cmath>

using namespace std;

int gcd (int x, int y)

{

while (x && y){

if (x > y)

x %= y;

else

y %= x;

}

return (x + y);

}

int main()

{

int x1, y1, x2, y2;

cout << "koncy otrezka" << endl;

cin >> x1 >> y1 >> x2 >> y2;

int a = abs(x1 - x2);

int b = abs(y1 - y2);

int k = gcd(a, b) + 1;

cout << "kol-vo = " << k;

return 0;

}

VI. Тэсціраванне.

Прыклад 7.11.

V. Праграма:

#include <iostream>

using namespace std;

int gcd (int x, int y)

{

while (x && y){

x %= y;

swap(x, y);

}

return (x + y);

}

int main()

{

int a;

cout << "kol-vo %" << endl;

cin >> a;

int b = 100 - a;

int k = 100 / gcd(a, b);

cout << "kol-vo = " << k << endl;

return 0;

}

VI. Тэсціраванне.

У дадзенай рэалізацыі алгарытму Эўкліда выкарыстана наступная ўласцівасць: НОД (x, y) = НОД (y, x). Функцыя swap(x, y) мяняе месцамі значэнні пераменных x і y.

7.4. Функции, возвращающие логический результат

Дастаткова часта пры рашэнні задач узнікае неабходнасць у праверцы розных умоў. Калі ўмова не складаная, то можна выкарыстоўваць каманду галінавання. Аднак на практыцы ўмовы могуць быць дастаткова складанымі. У гэтым выпадку можна апісаць дапаможны алгарытм, які выканае праверку ўмовы і верне значэнне true ці false у залежнасці ад таго, выканана ўмова ці не.

Прыклад 7.12. Дадзены два натуральныя лікі n і m (n < m). Вывесці ўсе лікі, якія належаць адрэзку [n; m] і задавальняюць наступную ўмову: у ліку няцотная колькасць лічбаў і сума лічбаў ліку кратная 5. Прадугледзець выпадак, калі такіх лікаў няма. Праверку аднаго ліку аформіць у выглядзе падпраграмы.

Этапы выканання задання

I. Зыходныя даныя: пераменныя n і m.

II. Вынік: лікі з прамежку ад n да m, якія задавальняюць умову задачы.

III. Алгарытм рашэння задачы.

1. Увод зыходных даных.
2. Для вызначэння наяўнасці шуканых лікаў будзем выкарыстоўваць лагічную пераменную p, папярэдне надаўшы ёй значэнне p = false.
3. У цыкле ад n да m.

3.1. Для праверкі апішам функцыю check, якая будзе правяраць лік. Вынікам функцыі будзе true або false.
3.2. Калі лік задавльняе ўмову, то выведзем яго.
3.3. Калі вывелі лік, то зменім значэнне пераменнай p на true.
4. Калі пасля заканчэння цыкла значэнне пераменнай p засталося false, то выведзем паведамленне, што шуканых лікаў на адрэзку няма.

IV. Апісанне пераменных: n и m — int, p — bool.

Прыклад 7.12.

V. Праграма:

#include <iostream>

using namespace std;

bool check(int x)

{

int k = 0, s = 0;

while (x > 0){

//сума лічбаў ліку

s += x % 10;

//колькасць лічбаў ліку

k++;

x /= 10;

}

if (k % 2 !=0 && s % 5 == 0)

return true;

else

return false;

}

int main()

{

int m, n, i;

cout << "n=";

cin >> n;

cout << "m=";

cin >> m;

bool p = false;

for (int i = n; i <= m; i++)

if (check(i)){

cout << i << " ";

p = true;

}

if (!p)

cout << "net chisel" << endl;

return 0;

}

VI. Тэсціраванне.

Паколькі функцыя для праверкі выніку мае тып bool і ўмова bool і ўмова (k % 2 != 0 && s % 5 == 0) у камандзе галінавання з’яўляецца выразам тыпу bool, то функцыя можа быць запісана наступным чынам:

bool prov(int x)

{

int k = 0, s = 0;

while (x > 0){

//сума лічбаў ліку

s += x % 10;

//колькасць лічбаў ліку

k++;

x /= 10;

}

return (k % 2 != 0 && s % 5 == 0);

}

7.5. Функцыі, якія не вяртаюць вынік

У мове Pascal выкарыстоўваюцца два віды дапаможных алгарытмаў: function і procedure. Функцыі, якія рэалізуюцца ў C++, з’яўляюцца аналагам function у Pascal. Аналагом procedure у мове С++ будуць функцыі, ў якіх тып значэння, якое вяртаецца, апісваецца ключавым словам void. Такія функцыі не вяртаюць якое-небудзь значэнне ў якасці выніку, таму ў канцы гэтых функцый адсутнічае каманда return.

Прыклад 7.13. Дадзены адрэзкі, даўжыні якіх роўныя a, b, c, d адпаведна. Для кожнай тройкі гэтых адрэзкаў, з якіх можна пабудаваць трохвугольнік, знайсці і вывесці плошчу гэтага трохвугольніка.

Этапы выканання задання

I. Зыходныя даныя: даўжыні адрэзкаў: a, b, c, d.

II. Вынік: плошчы магчымых трохвугольнікаў.

III. Алгарытм рашэння задачы.

1. Увод зыходных даных.
2. Для вызначэння, ці існуе трохвугольнік з даўжынямі старон x, y, z, о апішам лагічную функцыю prov.
3. Трохвугольнік існуе, калі сума даўжынь двух старон большая за трэцюю.
4. Для кожнага з магчымых набораў (a, b, c; a, b, d; a, c, d; b, c, d) праверым, ці існуе трохвугольнік, і калі функцыя prov верне true, то вылічым яго плошчу.
5. Плошчу будзем вылічваць з дапамогай функцыі plos, апісанай у прыкладзе 7.6.
6. Для вываду выніку апішам функцыю vyvod тыпу void.

IV. Апісанне пераменных: a, b, c, d — int.

Прыклад 7.13.

V. Праграма:

#include <iostream>

#include <cmath>

using namespace std;

double plos(double x, double y, double z)

{

double pr = (x + y + z) / 2;

double pl = sqrt(pr * (pr - x) * (pr - y) * (pr - z));

return pl;

}

bool prov (double x, double y, double z)

{

return (x < y + z && y < x + z && z < x + y);

}

void vyvod (double x, double y, double z)

{

cout << "storiny treugolnika: ";

cout << x << " " << y << " " << z;

cout << endl << "ploschad: ";

cout << plos(x, y, z) << endl;

}

int main()

{

double a, b, c, d;

cout << "a, b, c, d" << endl;

cin >> a >> b >> c >> d;

if (prov(a, b, c))

vyvod(a, b, c);

if (prov(a, b, d))

vyvod(a, b, d);

if (prov(a, c, d))

vyvod(a, c, d);

if (prov(b, c, d))

vyvod(b, c, d);

return 0;

}

VI. Тэсціраванне:

7.6. Рэкурсія

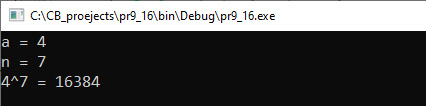
Рэкурсія — у праграмаванні выклік падпраграмы (прама ці ўскосна) з яе ж самой. Колькасць укладзеных выклікаў падпраграмы называюць глыбінёй рэкурсіі.

Адрозніваюць прамую (простую, непасрэдную) і ўскосную (складаную, апасродкаваную) рэкурсію.

Прамая рэкурсія: пры апісанні функцыі выкарыстоўваецца зварот да яе ж самой, але з іншым наборам параметраў.

Ускосная рэкурсія: падпраграма выклікае якую-небудзь іншую падпраграму, у апісанні якой змяшчааецца выклік зыходнай (напрыклад, функцыя A выклікае функцыю B, а функцыя B выклікае функцыю A). Ускосны выклік можа быць арганізаваны і больш складаным чынам, г. зн. у рэкурсію могуць быць уключаны некалькі падпраграм.

Рэкурсіўная праграма дазваляе апісаць паўтаральныя дзеянні без відавочных паўтораў частак праграмы і выкарыстання цыклаў.

Структура рэкурсіўнай функцыі змяшчае каманду галінавання. Умова ў гэтай камандзе вызначае, калі рэкурсія павінна спыніцца. Па адной з галін гэтай каманды павінен адбывацца хоць бы адзін рэкурсіўны выклік (прамы ці ўскосны) функцыяй самой сябе. Правільна напісаная рэкурсіўная функцыя павінна гарантаваць, што праз канечную колькасць рэкурсіўных выклікаў будзе дасягнута выкананне ўмовы спынення рэкурсіі, у выніку чаго ланцуг паслядоўных рэкурсіўных выклікаў перапыніцца і выканаецца вяртанне.

Любая рэкурсіўная функцыя можа быць рэалізавана не рэкурсіўна.

Прыклад 7.14. Апісаць алгарытм Эўкліда з дапамогай рэкурсіўнай функцыі.

Этапы выканання задання

I. Зыходныя даныя: два лікі a, b.

II. Вынік: НОД (a, b).

III. Алгарытм рашэння задачы.

1. Увод зыходных даных.
2. Умовай спынення рэкурсіі будзе роўнасць лікаў. Калі лікі не роўныя, то выклікаем саму функцыю gcd. Пры гэтым адзін з параметраў замяняем на рознасць.
3. Вывад выніку.

IV. Апісанне пераменных: a, b, c, d — int.

Прыклад 7.15. Напісаць праграму, якая выводзіць раскладанне ліку на простыя множнікі.

Этапы выканання задання

I. Зыходныя даныя: число n.

II. Вынік: простыя множнікі ліку a.

III. Алгарытм рашэння задачы.

1. Увод зыходных даных.
2. Для атрымання раскладання лік трэба па чарзе спрабаваць дзяліць на простыя лікі: 2, 3, 5... . Калі падзяліўся, то дадзены лік уваходзіць у раскладанне і трэба паспрабаваць падзяліць на яго атрыманую дзель, калі не, то паспрабуем дзяліць на наступны просты. Працэс заканчваецца, калі ў дзелі атрымліваем 1.
3. Апішам рэкурсіўную функцыю razlog(a, b).

3.1. Параметр а — лік, які спрабуем дзяліць, параметр b — лік, на які спрабуем дзяліць.
3.2. Умова спынення рэкурсіі — параметр a роўны 1.
3.3. . Калі a дзеліцца на b, то пры выкліку функцыі першы параметр замяняем дзеллю a / b, калі не, то другі параметр павялічваем на 1.
3.4. Пры такой арганізацыі вылічэнняў можна не правяраць, што бягучы дзельнік з’яўляецца простым лікам, паколькі ні на адно састаўное бягучае значэнне першага параметру падзяліцца не зможа.
3.5. Вывад выніку будзе ажыццяўляцца пры звяртанні з рэкурсіі.

IV. Апісанне пераменных: n — int.

З дапамогай рэкурсіі зручна рэалізоўваць рашэнне такіх задач, у якіх сам алгарытм, што рэалізоўваецца, у сутнасці рэкурсіўны. Дастаткова проста апісаць рэкурсіўную функцыю, калі рашэнне задачы можа быць апісана з дапамогай рэкурэнтных суадносін.

Прыклад 7.16. Па азначэнні . Гэта значыць для таго, каб знайсці значэнне aⁿ неабходна выканаць n – 1 множянняў. Алгарытм хуткага (бінарнага) узвядзення ў ступень дазваляе скараціць колькасць множанняў. Алгарытм (для n ≥ 0) можа быць апісаны з дапамогай наступных рэкурэнтных суадносін:

$a to the power of n space equals space open curly brackets table attributes columnalign left end attributes row cell 1 comma space a space equals space 0 end cell row cell open parentheses a to the power of n over 2 end exponent close parentheses squared comma space space space a space space long dash space цотнае end cell row cell a space space asterisk times space a to the power of n space – space 1 end exponent comma space space n space long dash space няцотнае end cell end table close$

Напісаць праграму, якая знаходзіць aⁿ, выкарыстоўваючы апісаны вышэй алгарытм.

Этапы выканання задання

I. Зыходныя даныя: числа a і n.

II. Вынік: значэнне aⁿ.

III. Алгарытм рашэння задачы.

1. Увод зыходных даных.
2. Апішам рэкурсіўную функцыю binpow(x, k).

2.1. Параметр x — аснова ступені, параметр k — паказчык.
2.2. Умова спынення рэкурсіі — параметр k роўна 0. Функцыя павінна вярнуць 1.
2.3. Калі k — цотны, то пры выкліку функцыі другі параметр памяншаем у 2 разы, калі няцотны, то другі параметр памяншаем на 1.

3. Вывад выніку.

IV. Апісанне пераменных: a, n — int.

У некаторых дэкларатыўных або чыста функцыянальных мовах (такіх як Пралог ці Haskell) няма сінтаксічных сродкаў для арганізацыі цыклаў. У іх рэкурсія з’яўляецца адзіным даступным механізмам для арганізацыі паўтаральных вылічэнняў.

Пытанне пра пажаданасць выкарыстання рэкурсіўных функцый у праграміраванні неадназначны: з аднаго боку, рэкурсіўная форма можа быць структурна больш простай і нагляднай, асабліва калі сам рэалізуемы алгарытм у сутнасці рэкурсіўны. З іншага боку, звычайна рэкамендуецца пазбягаць рэкурсіўных праграм, якія прыводзяць (ці ў некаторых умовах могуць прыводзіць) да занадта вялікай глыбіні рэкурсіі.

Класічным прыкладам бясконцай рэкурсіі з’яўляюцца два пастаўленыя адно насупраць аднаго люстэркі: у іх утвараюцца два калідоры з адлюстраванняў люстэркаў, якія памяншаюцца.

Рэкурсія ляжыць у аснове пабудовы фрактальных малюнкаў.

Прыклад 7.14.

V. Праграма:

#include <iostream>

using namespace std;

int gcd (int x, int y)

{

if (x == y)

return x;

else

if (x > y)

gcd(x - y, y);

else

gcd(x, y - x);

}

int main()

{

int a, b;

cout << "vvedi 2 chisla" << endl;

cin >> a >> b;

int d = gcd(a, b);

cout << "NOD = " << d << endl;

return 0;

}

VI. Тэсціраванне:

Рэкурсіўная функцыя для вылічэння НАД двух лікаў можа быць запісана з выкарыстаннем тэрнарнай (ад лац. ternarius — трайны) умоўнай аперацыі.

int gcd (int a, int b)

{

return b ? gcd (b, a % b) : a;

}

Аперацыя, якая структурна запісваецца як o1 : o2 : o3, вяртае свой другі (o2) або трэці (o3) аперанд у залежнасці ад значэння лагічнага зададзенага выразу, зададзенага першым аперандам (o1).

Прыклад 7.15.

V. Праграма:

#include <iostream>

using namespace std;

void razlog (int a, int b)

{

if (a > 1)

if ( a % b == 0){

razlog(a / b, b);

cout << b << " ";

}

else

razlog(a, b + 1);

}

int main()

{

int n;

cout << "n = ";

cin >> n;

razlog(n, 2);

return 0;

}

VI. Тэсціраванне:

VII. Аналіз выніку.

Каб зразумець, чаму мы перабіраем простыя множнікі, пачынаючы з меншага, а праграма выводзіць іх у адваротным парадку, распішам парадак выканання каманд у праграме.

№	a	b	Каментарыі
1	60	2	a > 1, 60 % 2 = 0, выклік (60 / 2, 2), пасля выкліку ёсць каманда вываду
2	30	2	a > 1, 30 % 2 = 0, выклік (30 / 2, 2), пасля выкліку ёсць каманда вываду
3	15	2	a > 1, 15 % 2 ≠ 0, выклік (15, 3) пасля выкліку няма каманд
4	15	3	a > 1, 15 % 3 = 0, выклік (15 / 3, 3), пасля выкліку ёсць каманда вываду
5	5	3	a > 1, 5 % 3 ≠ 0, выклік (5, 4), пасля выкліку няма каманд
6	5	4	a > 1, 5 % 4 ≠ 0, выклік (5, 5), пасля выкліку няма каманд
7	5	5	a > 1, 5 % 5 = 0, выклік (5 / 5, 5), пасля выкліку ёсць каманда вываду
8	1	5	умова a > 1 не выконваецца; пры гэтым выкліку функцыя скончыла работу, аднак не скончана работа пры тых выкліках, пасля якіх ёсць вывад.
9	5	5	вывад b = 5
10	15	3	вывад b = 3
11	30	2	вывад b = 2
12	60	2	вывад b = 2

СЗахаванне выклікаў рэкурсіўнай функцыі разам са значэннямі параметраў і адрасам звяртання забяспечвае механізм стэка [1] выклікаў. Кожны рэкурсіўны выклік патрабуе некаторай колькасці аператыўнай памяці кампутара, таму пры празмеру вялікай глыбіні рэкурсіі можа наступіць перапаўненне стэка выклікаў.

Прыклад 7.16.

V. Праграма:

#include <iostream>

using namespace std;

int binpow(int x, int k)

{

if (k == 0)

return 1;

if (k % 2 == 1)

return binpow(x, k-1) * x;

else {

int b = binpow(x, k / 2);

return b * b;

}

int main()

{

int a, n;

cout << "a = ";

cin >> a;

cout << "n = ";

cin >> n;

cout << a << "^" << n << " = ";

cout << binpow(a, n) << endl;

return 0;

}

VI. Тэсціраванне:

[1] З паняццем стэка вы пазнаёміцеся пазней.

Пытанні к параграфу

1. Што такое дапаможны алгарытм?

2. Як называюць дапаможны алгарытм, запісаны на мове праграміравання?

3. Якія падпраграмы рэалізаваны ў мове С++?

4. Які фармат мае абвяшчэнне функцыі ў С++?

5. Дзе змяшчаецца азначэнне функцыі?

6. Што такое фармальныя параметры? Што такое фактычныя параметры?

7. Што разумеюць пад рэкурсіяй?

Практыкаванні

1. Напішыце праграмы для рашэння задач. Аформіце вылічэнне пералічаных функцый у якасці падпраграм.

Дадзена рэчыўнае значэнне x. Артымаць

$f space left parenthesis 2 x comma space 3 right parenthesis space plus space f space left parenthesis 3 comma 5 space – space x right parenthesis comma space дзе space f space left parenthesis a comma space b right parenthesis equals fraction numerator 2 a space – b over denominator 5 space – space a end fraction.$

2. Дадзены рэчыўныя значэнні t і s. Атрымаць

$f space left parenthesis t comma space – space 2 s comma space 1.17 right parenthesis space plus space f space left parenthesis 2.2 comma space t comma space t space – space s right parenthesis comma space дзе space f space left parenthesis a comma space b comma space c right parenthesis equals fraction numerator 2 a space – b space plus space square root of c over denominator 5 space plus space open vertical bar с close vertical bar end fraction.$

3. Дадзены рэчаісны лік y. Атрымаць

$fraction numerator 1.7 f space left parenthesis 0.25 comma space 3 right parenthesis space plus 2 space f space left parenthesis 1 plus y comma space 4 right parenthesis over denominator 6 space – space f left parenthesis y squared space – space 2 comma space 5 right parenthesis end fraction comma space дзе space f space left parenthesis x comma space k right parenthesis equals fraction numerator x to the power of 2 k space plus space 1 end exponent over denominator left parenthesis 2 k right parenthesis factorial end fraction.$

2. Напішыце праграмы для рашэння задач, выкарыстоўваючы толькі функцыі, апісаныя ў прыкладзе 7.5, і арыфметычныя дзеянні (нельга выкарыстоўваць галінаванні, цыклы і іншыя функцыі).

1. Дадзены тры розныя лікі. Вывесці той, які не роўны мінімальнаму і не роўны максімальнаму з уведзеных лікаў.

Падказка. Ад сумы трох лікаў адняць мінімальнае і максімальнае.

2. Дадзены чатыры розныя лікі. Вывесці іх у парадку ўзрастання.

Падказка. Знайсці min(max(a, b)), max(c, d) і max(min(a, b)), min(c, d).

3⃰. Дадзены пяць розных лікаў. Вывесці ў парадку спадання тыя тры з іх, якія не супадаюць з мінімальным і максімальным з уведзеных лікаў.

3. Напішыце праграмы для рашэння геаметрычных задач.

1. Трохвугольнік зададзены каардынатамі сваіх вяршынь. Знайсці перыметр трохвугольніка. Вылічэнне даўжыні адрэзка аформіць у выглядзе падпраграмы.
2. Чатырохвугольнік зададзены каардынатамі сваіх вяршынь. Знайсці перыметр чатыровугольніка. Вылічэнне даўжыні адрэзка аформіць у выглядзе падпраграмы.
3. Выпуклы чатырохвугольнік зададзены даўжынямі сваіх старон і дыяганаллю. Знайсці плошчу чатыровугольніка як суму плошчаў двух трохвугольнікаў. Вылічэнне плошчы трохвугольніка аформіць у выглядзе падпраграмы.
4. Выпуклы пяцівугольнік зададзены даўжынямі сваіх старон і дзвюма дыяганалямі, праведзенымі з адной вяршыні. Знайсці плошчу пяцівугольніка як суму плошчаў трох трохвугольнікаў. Вылічэнне плошчы трохвугольніка аформіць у выглядзе падпраграмы.

4. У прыкладах 7.9, 7.10, 7.11 і 7.14 прыведзены розныя рэалізацыі алгарытму Эўкліда. Пратэсціруйце гэтыя алгарытмы на розных наборах лікаў. Параўнайце час работы алгарытмаў. Час можна паглядзець у кансольным акне (праграму скампілюйце ў рэжыме debug).

1. Перабярыце значэнні а і b ад 2 да 100 000. Знайдзіце НАД(a, b) для ўсіх магчымых пар. Значэнні а і b абодва ўзрастаюць ад 2 да 100 000.
2. Перабярыце значэнні а і b ад 2 да 100 000. Знайдзіце НАД(a, b) для ўсіх магчымых пар. Значэнні a ўзрастаюць ад 2 да 100 000, значэнні b спадаюць ад 100 000 да 2.
3. Значэнні а і b атрымліваюць выпадковым чынам. Колькасць значэнняў [2; 1000].
4. Значэнні а і b атрымліваюць выпадковым чынам. Колькасць значэнняў 100 000, дыяпазон [2; 1 000 000].

5. Выкарыстоўваючы функцыю для вылічэння НАД(a, b), рашыце наступныя задачы:

1. Напішыце праграму, якая знойдзе НАД чатырох лікаў.
2. Напішыце праграму, якая знойдзе НАК (найменшае агульнае кратнае) двух лікаў.
3. Уводзяцца лічнік і назоўнік правільнага дробу. Напішыце праграму, якая скароціць дроб.
4. Два правільныя дробы зададзены сваімі лічнікамі і назоўнікамі. Напішыце праграму, якая знойдзе іх суму. Адказ выведзіце ў выглядзе змешанага дробу.
5. Зададзены два натуральныя лікі ў дзесятковай сістэме лічэння, якія складаюцца з адзінак. У першым ліку роўна n адзінак, а ў другім іх роўна m. Уводзяцца лікі n і m. Напішыце праграму, якая знойдзе НАД лікаў, якія складаюцца з n і m адзінак адпаведна.
6. Каця вырашыла запрасіць да сябе ў госці n сяброў. Паколькі яе сябры вельмі любяць садавіну, то ў якасці пачастунка для іх яна купіла m аднолькавых апельсінаў. Яна жадае разразаць кожны апельсін на аднолькавы лік роўных частак так, каб іх можна было размеркаваць паміж гасцямі (сама Каця апельсіны есці не будзе) і ўсім гасцям дасталася пароўну частак. Напішыце праграму, якая вылічвае мінімальную колькасць частак, на якую неабходна разразаць кожны апельсін, каб былі выкананы названыя вышэй умовы. Прыклад: пры n = 2, m = 5 адказ 2.
7. Паралель дзясятых класаў напісала кантрольную работу. У выніку роўна a % навучэнцаў атрымалі «выдатна», роўна b % — «добра», роўна c % —«задавальняюча», а астатнія d % напісалі кантрольную незадавальняюча. Якая мінімальная колькасць навучэнцаў павінна быць у паралелі дзясятых класаў для таго, каб маглі атрымацца такія вынікі? Уводзяцца 4 цэлыя лікі ад 0 да 100:
a, b, c, d (a + b + c + d = 100). Выведзіце адзіны цэлы дадатны лік — мінімальную магчымую колькасць навучэнцаў у паралелі.

6. Дадзены два натуральныя лікі n і m (n < m). Напісаць праграму, якая выведзе ўсе лікі, што належаць адрэзку [n; m] і задавальняюць умовы, апісаныя ніжэй. Прадугледзець выпадак, калі такіх лікаў няма. Праверку аднаго ліку аформіць у выглядзе падпраграмы.

1. Лік з’яўляецца «добрым». (Натуральны лік назавём добрым, калі ён дзеліцца на суму сваіх лічбаў.)
2. Лічбы ліку размешчаны ў парадку ўзрастання.
3. Лік з’яўляецца паліндромам цотнай даўжыні.
4. Лік з’яўляецца «шчаслівым» — сума лічбаў ліку, якія стаяць на першых k месцах, роўна суме лічбаў ліку, што стаяць на апошніх k месцах. (k —палова колькасці лічбаў ліку.)
5. Лік з’яўляецца «шчаслівым» — сума лічбаў ліку, якія стаяць на няцотных месцах, роўна суме лічбаў ліку, што стаяць на цотных месцах.
6. Лік з’яўляецца лікам Армстранга. (Натуральны лік з k лічбаў з’яўляецца лікам Армстранга, калі сума яго лічбаў, узведзеных у k-ю ступень, роўна самаму ліку, напрыклад 153 = 1³+ 5³+ 3³, k = 3.)
7. Лік з’яўляецца трохвугольным. (Трохвугольны лік — колькасць кружкоў, якія могуць быць расстаўлены ў форме правільнага трохвугольніка. Паказваецца ў выглядзе $fraction numerator k left parenthesis k space plus space 1 right parenthesis over denominator 2 end fraction$ , напрыклад лік $begin mathsize 16px style 15 space equals space fraction numerator 5 space asterisk times space 6 over denominator 2 end fraction end style$ .)

7. Напішыце праграмы для рашэння задач, аформіўшы патрэбныя падпраграмы.

1. Трохвугольнік зададзены даўжынямі сваіх старон. Знайсці даўжыні яго вышынь.
2. Дадзены каардынаты вяршынь трохвугольніка і каардынаты некаторага пункта ўнутры яго. Знайсці адлегласць да бліжэйшай стараны трохвугольніка.

Падказка. Гэта адлегласць з’яўляецца вышынёй аднаго з атрыманых трохвугольнікаў.

3. Дадзены каардынаты вяршынь чатырохвугольніка і каардынаты некаторага пункта ўнутры яго. Знайсці адлегласць да найбліжэйшай вяршыні чатырохвугольніка.
4. Тры прамавугольніка са старанамі, паралельнымі восям каардынат, зададзены каардынатамі сваіх дыяганалей. Выпісаць усе чатыры вяршыні для кожнага з прамавугольнікаў і знайсці іх плошчы.
5. Два прамавугольнікі са старанамі, паралельнымі восям каардынат, зададзены каардынатамі сваіх дыяганалей. Праверыць, ці дакладна, што прамавугольнік з меншай плошчай цалкам знаходзіцца ўнутры прамавугольніка з большай плошчай. Калі «так», то знайсці плошчу атрыманай «рамкі».

§ 7. Паняцце дапаможнага алгарытму

Оглавление

7.1. Дапаможныя алгарытмы

7.2. Функцыі, якія вяртаюць лікавы вынік

7.3. Найбольшы агульны дзельнік двух лікаў

7.4. Функции, возвращающие логический результат

7.5. Функцыі, якія не вяртаюць вынік

7.6. Рэкурсія

Пытанні к параграфу

Практыкаванні