Печатать книгуПечатать книгу

§ 6. Выкарыстанне асноўных алгарытмічных канструкцый для рашэння задач

Сайт: Профильное обучение
Курс: Інфарматыка. 10 клас (Павышаны ўзровень)
Книга: § 6. Выкарыстанне асноўных алгарытмічных канструкцый для рашэння задач
Напечатано:: Гость
Дата: Пятница, 6 Июнь 2025, 06:37

Оглавление

6.1. Наладка праграм у асяроддзі Code::Blocks

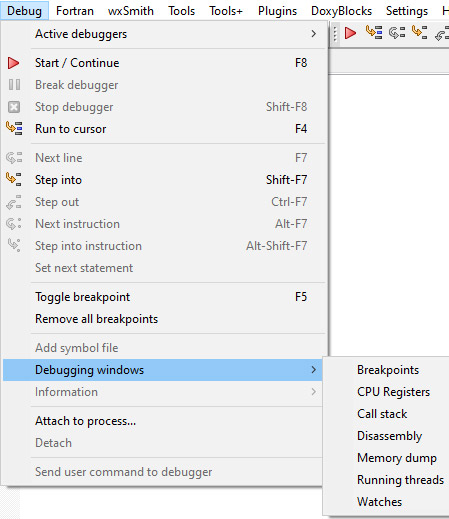
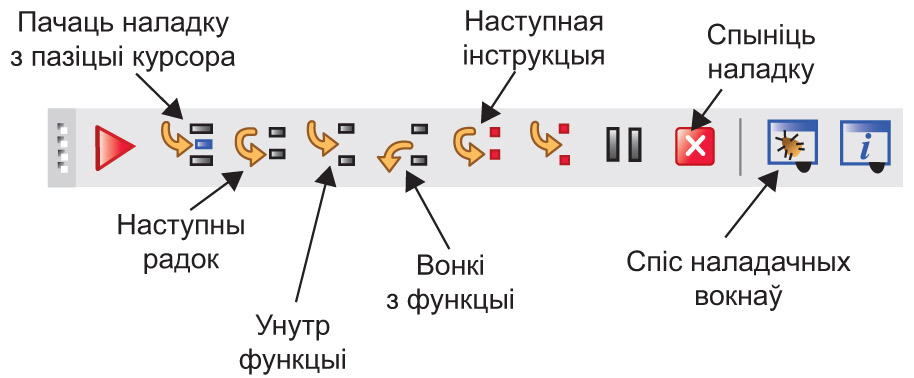
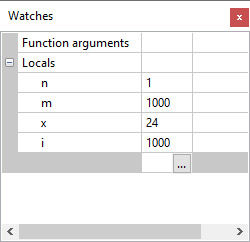
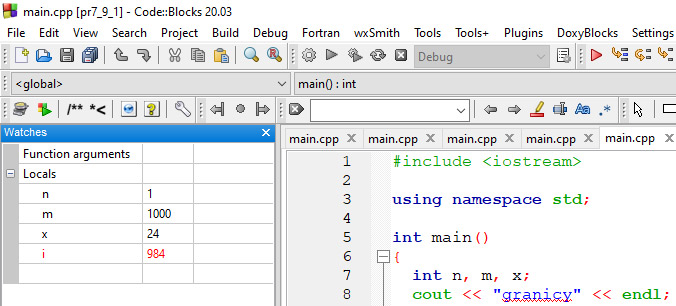
У дапамогу карыстальніку амаль любога асяроддзя праграміравання даюцца сродкі, неабходныя для наладкі праграмы. Яны дазваляюць старанна пратэсціраваць праграму і выправіць усе памылкі ў ёй  (прыклад 6.1). Асяроддзе Code::Blocks змяшчае наладчык, які дазваляе выканаць праграму па радках, праглядаць і мадыфікаваць пераменныя і выразы. Адладчык убудаваны ў інтэграванае асяроддзе, і таму карыстальнік можа рэдагаваць, кампіляваць і адладжваць праграму, не выходзячы з асяроддзя.

Памылкі кампіляцыі

Памылкі кампіляцыі, або сінтаксічныя памылкі, узнікаюць у тым выпадку, калі не апісана некаторая пераменная, перадаецца няправільная колькасць параметраў функцыі, прапушчана кропка з коскай ці дужка і г. д. З выпраўленнем памылак, выяўленых у час кампіляцыі, складанасцей практычна не ўзнікае. Кампілятар, выявіўшы ў праграме памылкі, завяршае працу і выдае інфармацыю пра памылкі ў акне рэдактара кода, на ўкладцы Build log (прыклад 6.2). Исправив ошибки, обнаруженные таким образом, можно повторить компиляцию программы.

Памылкі выканання

Памылкі выканання, або семантычныя памылкі, узнікаюць на этапе выканання пры спробе адкрыць файл, якога не існуе, дзяліць на нуль і г. д. (прыклад 6.3). Пры гэтым выкананне праграмы перарываецца. Узнікненне фатальных памылак прыводзіць да неадкладнага спынення выканання праграмы.

Лагічныя памылкі

Праграма можа змяшчаць і лагічныя памылкі. Лагічныя памылкі дазваляюць кампілятару выканаць праграму, аднак вынік выканання будзе адрознівацца ад чаканага. Наяўнасць такіх памылак вызначаецца з дапамогай тэсціравання. Выявіць памылку гэтай групы, не маючы ніякіх наладачных сродкаў, бывае дастаткова складана. Наяўнасць у праграме такіх памылак з’яўляецца адной з асноўных прычын узнікнення неабходнасці выкарыстання наладчыка, які ўваходзіць у склад інтэграванага асяроддзя. Наладчык дазваляе выканаць праграму ў дыялогавым рэжыме, назіраючы за змяненнем значэнняў асобных пераменных ці выразаў. Маецца магчымасць спыніцца ў зададзеным пункце праграмы і змяніць значэнні некаторых пераменных і выразаў.

Каманды наладчыка сабраны ў меню Debug (прыклад 6.4). Гэтыя ж каманды прадубляваны на панэлі хуткага доступу  (прыклад 6.5). Апісанне каманд наладкі, сабраных у меню Debug, прыведзены ў  Дадатку да главы 1.

Трасіроўка — выкананне зыходнай праграмы па радках, пры якім пасля выканання кожнага радка можна спыніцца і паглядзець вынікі.

Наяўнасць магчымасці выканання зыходнай праграмы да радка, на які паказвае курсор, дазваляе прапусціць трасіроўку малацікавых частак праграмы і адразу перайсці ў пункт пачатку наладкі. Для гэтых мэт можна націснуць F4 у радку з курсорам. Калі гэты радок знаходзіцца пасля ўводу даных, то ўвод даных адбудзецца як звычайна, выкананне праграмы перапыніцца, калі прыйдзе чарга выканання гэтага радка. Неабходна пераключыцца з кансольнага акна ў акно кода. Той радок, які павінен выканацца, пазначаецца жоўтым трохвугольнікам   (прыклад 6.6).

Некаторыя радкі праграмы могуць быць пазначаны як пункты перарывання. Для гэтага дастаткова клікнуць мышшу злева ад радка праграмы. У гэтым месцы з’явіцца чырвоны круг  (прыклад 6.7).

Калі ў працэсе выканання аладкі праграмы (запуск з дапамогай клавішы F8 ці ) дасягаецца пункт перарывання, выкананне праграмы прыпыняецца і на экране адлюстроўваецца фрагмент зыходнага тэксту праграмы, які змяшчае пункт перарывання. Па-над пунктам перарывання ўстанаўліваецца маркер наладкі праграмы  . Спыніўшыся ў пункце перарывання, можна прагледзець значэнні пераменных, пачаць трасіроўку ці выканаць праграму да наступнага пункта перарывання.

Наладчык інтэграванага асяроддзя Code::Blocks дае магчымасць назірання за змяненнем пераменных ці выразаў. Аб’екты, за якімі назіраюць, адлюстроўваюцца ў акне назірання Watches, паказваючы змяненні ў праграме пры пакрокавым выкананні. Для адкрыцця акна Watches можна выканаць каманду Debug → ebugging Windows → Watches ці выбраць яго са спісу наладачных вокнаў на панэлі хуткага доступу  (прыклад 6.8).

Для дабаўлення пераменнай у акно прагляду трэба дабавіць яе імя ў першы слупок акна Watches. 

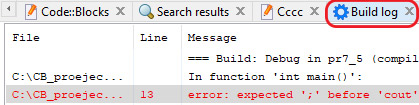
Прыклад 6.1. Тыпы памылак:

  • памылкі кампіляцыі (сінтаксічныя);
  • памылкі выканання;
  • лагічныя памылкі.

Пыклад 6.2. Прыклад памылкі кампіляцыі.

Усе памылкі вылучаюцца чырвоным колерам. Для кожнай памылкі паказваецца нумар радка, у якім выяўлена памылка, і апісанне гэтай памылкі. Шэрым фонам падсвечваецца тая з памылак, якая вылучана ў праграме знакам   .

Двайная пстрычка па памылцы ў акне Build log пакажа яе месцазнаходжанне ў праграме. Пераходзіць да прагляду наступнай памылкі можна з выкарыстаннем спалучэння клавіш

Alt + F2, а вярнуцца да папярэдняй — Alt + F1.

Прыклад 6.3. Прыклад памылкі выканання.

Тэкст праграмы:

#include <iostream>

 

using namespace std;

 

int main()

{

    int x;

    cout << "x = ";

    cin >> x;

    int y = x / (x - 5);

    cout << y;

    return 0;

}

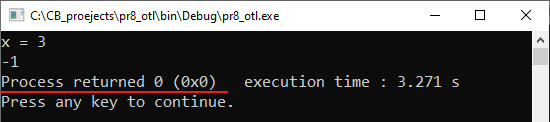
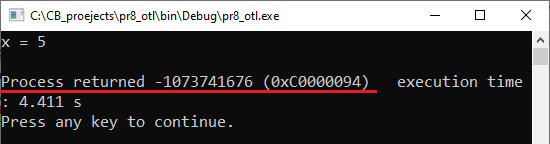
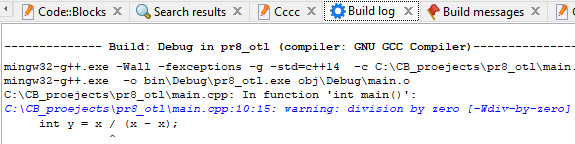
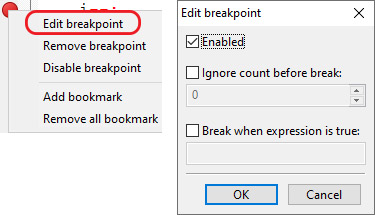
Тэсціраванне:

Пры x = 5 узнікае памылка дзялення на нуль, і асяроддзе выдае паведамленне з кодам памылкі: «Process returned –1073741676». Калі праграма выканалася паспяхова, то код памылкі 0: «Process returned 0».

Пры аналізе праграмы кампілятар выдае не толькі памылкі, але і папярэджанні (warning) пра тое, што некаторыя запісы могуць прывесці да памылкі. Папярэджанні вылучаюцца сінім колерам.

Калі ў праграме вышэй запісаць 

    int y = x / (x - x);   

то пры кампіляцыі праграмы можна ўбачыць папярэджанне:

Прыклад 6.4. Меню  Debug:

Прыклад 6.5. Панэль хуткага доступу з камандамі наладкі:

  Прыклад 6.6. Рэжым наладкі:

Прыклад 6.7. Пункты перарывання:

Калі пункт перарывання ўстаноўлены ўнутры цыкла, то можна вызначыць, колькі ітэрацый цыкла будзе прапушчана, перад тым як праграма перапыніцца. Зрабіць гэта можна з кантэкставага меню пункта перарывання. Таксама можна паказаць лагічны выраз, пры якім спрацуе пункт перарывання.

Прыклад 6.8. Акно назірання за значэннямі пераменных  Watches:

Акно Watches з’яўляецца «вісячым», пры жаданні яго можна прычапіць да акна рэдактара кода. Для гэтага трэба перамясціць акно Watches да акна рэдактара кода і выбраць месца яго змяшчэння. У працэсе перамяшчэння акна месца, куды яго можна «прычапіць», будзе адлюстроўвацца прамавугольнікам шэрага колеру.

У акне Watches адлюстроўваюцца бягучыя значэнні пераменных. Пераменная, якая змянілася апошняй, адлюстроўваецца чырвоным колерам.

6.2. Выкарыстанне лікавых паслядоўнасцей

Лікавыя паслядоўнасці дазваляюць апісваць шмат якія працэсы, што адбываюцца ў прыродзе і грамадстве. Для задання элементаў лікавай паслядоўнасці звычайна выкарыстоўваюць адзін з двух спосабаў:

1. Запісваецца залежнасць значэння элемента паслядоўнасці ад значэння нумара  (прыклад 6.9).
2. Запісваецца рэкурэнтная формула залежнасці значэння элемента ад значэння аднаго ці некалькіх папярэдніх значэнняў  (прыклад 6.10).

Ёсць паслядоўнасці, якія можна задаваць як першым спосабам, так і другім (прыклад 6.11).

Паслядоўнасці могуць будавацца з выпадковых лікаў.

Прыклад 6.12. Вывесці на экран першыя k элементаў паслядоўнасці, зададзенай формулой   begin mathsize 18px style a subscript n space equals space fraction numerator n over denominator n squared space plus space 1 end fraction end style.

Этапы выканання задання

I. Зыходныя даныя: k (колькасць лікаў).

II. Вынік: k лікаў паслядоўнасці.

III. Алгарытм рашэння задачы.

1. Увод ліку k. 
2. Паколькі колькасць лікаў загадзя вядомая, то для іх атрымання можна выкарыстаць цыкл  for. 
3. Бягучы лік будзем захоўваць у пераменнай а. Значэнне a вылічваецца па формуле і залежыць ад значэння n — лічыльніка цыкла. Пераменная n будзе змяняцца ад 1 (нумар першага цотнага ліку) да k (нумар апошняга ліку). 
4. Атрыманыя лікі будзем выводзіць у цыкле праз прабел.

IV. Апісанне пераменных: k – int, n – double.

Прыклад 6.13. Знайсці першы элемент паслядоўнасці, зададзенай рэкурэнтна a subscript n space equals space fraction numerator a subscript n space minus space 1 over denominator cube root of 2 n squared end root end fraction comma space space space a 1 space equals space b left parenthesis b space greater than space 0 right parenthesis; меншы за 10−3. Таксама вывесці нумар знойдзенага элемента. Значэнне b уводзіцца.

Этапы выканання задання

I.Зыходныя даныя: лік b.

II. Вынік: элемент паслядоўнасці, меншы за 0.001, і яго нумар.

III. Алгарытм рашэння задачы.

1.Увод ліку b.
2. Паколькі вядома ўмова працягвання работы, то выкарыстаем цыкл  while. Умова цыкла: a >= 0.001.
3. У цыкле вылічваем бягучае значэнне a і павялічваем на 1 нумар шуканага значэння.
4. Вывад выніку.

IV. Апісанне пераменных: a, b – double, n - int.

Пацверджаннем важнасці лікавых паслядоўнасцей з’яўляецца той факт, што створана цэлая энцыклапедыя лікавых паслядоўнасцей OEIS [1].

Прыклад 6.9. Формула  begin mathsize 14px style a subscript n space equals space fraction numerator n over denominator n squared space plus space 1 end fraction end style задае наступную паслядоўнасць: 0.5, 0.4, 0.3, 0.235, 0.192, … .

Прыклад 6.10. Адной з найбольш вядомых паслядоўнасцей, якую можна апісаць рэкурэнтна, з’яўляецца паслядоўнасць Фібаначы: 1, 1, 2, 3, 5, 8, 13… . Нескладана заўважыць, што кожны яе элемент, пачынаючы з трэцяга, роўны суме двух папярэдніх. Гэта можна запісаць так: an = an − 1 + an − 2, a1 = 1,  a2 =1.

Прыклад 6.11. У паслядоўнасці 2, 4, 8, 16,… кожны лік з’яўляецца ступенню 2, таму яе можна задаць формулай an = 2n. З іншага боку, кожны элемент паслядоўнасці, пачынаючы з другога, у два разы большы за папярэдні. Атрымаем формулу an = 2an − 1 (для n > 1, a1 = 2).

Прыклад 6.12.

V. Праграма:

#include <iostream>

 

using namespace std;

 

int main()

{

  int k;

  cout << "k = ";

  cin >> k;

  for (int n = 1; n <= k; n++){

    double a = 1. * n / (n * n + 1);

    cout << a << endl;

  }

  return 0;

}

VI. Тэсціраванне.

Пры вылічэнні значэння a важна памятаць, што вынікам дзялення двух цэлых лікаў (у дадзеным выпадку гэта лікі n і n2 + 1) будзе цэлы лік, таму неабходна пераўтварэнне тыпу ў рэчыўны да выканання аперацыі дзялення. Радок, у якім вылічваецца значэнне a, можна запісаць і так:

  double a = static_cast<double> n) / (n * n + 1);

Прыклад 6.13.

V. Праграма:

#include <iostream>

#include <cmath>

 

using namespace std;

 

int main()

{

  double a, b;

  cout << "b = ";

  cin >> b;

  a = b;

  int n = 1;

  while (a > 0.001){

    n++;

    a = a / cbrt(2 * n * n);

  }

  cout << "n = " << n << endl;

  cout << "a = " << a << endl;

  return 0;

}

VI. Тэсціраванне.


[1] http://oeis.org/?language=russian — Онлайн-энцыклапедыя цэлалікавых паслядоўнасцей.

6.3. Вылічэнне значэння фактарыяла ліку

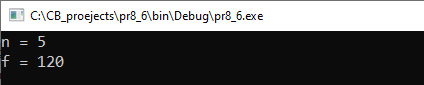
Фактарыялам ліку n называюць паслядоўны здабытак натуральных лікаў, не большых за  n:

n! = 1 · 2 · 3 · ... · n.

Роўнасць 0! = 1 звычайна прымаюць у якасці пагаднення.

Прымер 6.14. Напісаць праграму, якая па ўведзеным натуральным значэнні n атрымлівае n!.

Этапы выканання задання.

I. Для вылічэння : число n.

II. Вынік: f (значэнне n!).

III. Алгарытм рашэння задачы.

1. Ввод числа n.
2. Для вычисления n! трэба паслядоўна памнажаць на бягучы натуральны лік тое значэнне, якое атрымалі на папярэднім кроку. Гэта выцякае з роўнасці:

n! =(n – 1)! · n.

3. Для вылічэння здабытку можна выкарыстаць цыкл for. Пачатковае значэнне пераменнай  f роўна 1.
4. Вывад выніку S.

IV. Апісанне пераменных: n, f – int.

Назва фактарыял паходзіць ад лацінскага factorialis — які дзейнічае, выконвае, памнажае. У 1808 г. французскі матэматык Крысціян Крамп прапанаваў кампактнае абазначэнне  (вымаўляецца «эн фактарыя'л»).

Фактарыялы ўсіх лікаў складаюць паслядоўнасць A000142 у OEIS.

Прыклад 6.14.

V. Праграма:

#include <iostream>

 

using namespace std;

 

int main()

{

  int n;

  cout << "n = ";

  cin >> n;

  int f = 1;

  for (int i = 1; i <= n; i++)

    f *= i;

  cout << "f = " << f << endl;

  return 0;

}

VI. Тэсціраванне.

VII. Правільнасць вылічэнняў праверыць на калькулятары.

6.4. Знаходжанне сумы элементаў лікавай паслядоўнасці

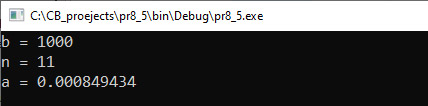
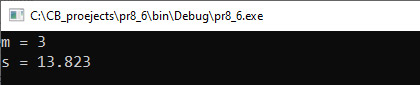
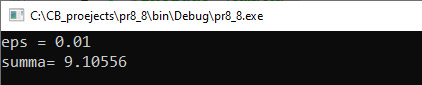
Прыклад 6.15. У сакрэтнай лабараторыі выводзяць карысныя бактэрыі. Эксперыментальна было вызначана, што колькасць бактэрый (у млн) залежыць ад нумара дня, у які праводзіцца эксперымент, наступным чынамм: begin mathsize 16px style a subscript n space equals fraction numerator n cubed over denominator square root of n cubed space minus space n space plus space 1 end root end fraction end style. Вызначыце, колькі бактэрый вывелі за m дзён.

Этапы выканання задання.

 I. Зыходныя даныяе: m (колькасць дзён).

II. Вынік: s (агульная колькасць бактэрый).

III. Алгарытм рашэння задачы.

1. Увод ліку m. 
2. Для вылічэння агульнай колькасці бактэрый неабходна паслядоўна прыбаўляць колькасць бактэрый, выведзеных у бягучы дзень, да ўжо атрыманай колькасці бактэрый. Пачатковае значэнне сумы роўна  0. 
3. Паколькі колькасць дзён загадзя вядомая, для вылічэння сумы можна выкарыстаць цыкл  for. 
4. Колькасць бактэрый у бягучы дзень будзем захоўваць у пераменнай а. Значэнне a залежыць ад значэння n — лічыльніка дзён. Пераменная n змяняецца ад 1 да m. 
5. Вывад выніку s.

IV. Апісанне пераменных: m – int, s, a – double.

Прыклад 6.16. Напісаць праграму для вылічэння сумы, якая мае сваімі складаемымі элементы паслядоўнасц begin mathsize 16px style a subscript n space equals space fraction numerator n space plus space 2 to the power of n over denominator n factorial end fraction end style. Вылічэнні выконваць да таго часу, пакуль не знойдзецца складаемае, для якога правільная няроўнасць begin mathsize 16px style open vertical bar a subscript n close vertical bar space less than space e p s end style. Значэнне eps уводзіцца (begin mathsize 16px style 0 space less than space e p s space less than space 1 end style).

Этапы выканання задання

I. Зыходныя даныя: eps (дакладнасць вылічэнняў).

II. Вынік: пераменная s (сума).

III. Алгарытм рашэння задачы.

1. Увод ліку eps. 
2. Для вылічэння сумы неабходна паслядоўна прыбаўляць чарговае складаемае, якое задавальняе ўмову задачы, да ўжо атрыманай сумы.

2.1. Паколькі колькасць складаемых загадзя не вядомая, то для вылічэння сумы выкарыстаем цыкл do…while. 
2.2. Пачатковае значэнне сумы s = 0.
2.3. Бягучае значэнне складаемага будзем захоўваць у пераменнай а. Значэнне a залежыць ад значэння n — лічыльніка складаемых у суме. Пераменная n будзе змяняцца на 1 да таго часу, пакуль выконваецца ўмова задачы. Пачатковае значэнне n = 0.
2.4. Асобна трэба атрымліваць 2n и n! Для гэтага завядзём пераменныя d (для захоўвання значэння 2n) і f (для захоўвання значэння n!). Пачатковыя значэнні пераменных: d = 1, f = 1. Для кожнага наступнага складаемага папярэдняе значэнне пераменнай d павялічваецца ў два разы, значэнне пераменнай f павялічваецца ў n раз.

3. Вывад вынік s.

IV. Апісанне пераменных: n – int, eps, a, s, d, f – double.

Прыклад 6.15.

V. Праграма:

#include <iostream>

#include <cmath>

 

using namespace std;

 

int main()

{

  int m;

  cout << "m = ";

  cin >> m;

  double s = 0;

  for (int n = 1; n <= m; n++){

    double x = 1. * n * n * n;

    double a = x / (sqrt(x)- n + 1);

    s += a;

  }

  cout << "s = " << s << endl;

  return 0;

}

VI. Тэсціраванне

VII. Аналіз выніку. Для праверкі правільнасці выніку можна палічыць значэнне сумы на калькулятары:

begin mathsize 14px style a subscript italic 1 space equals space 1 semicolon end style

begin mathsize 14px style a subscript 2 space equals space fraction numerator 2 cubed over denominator square root of 8 space minus space 2 space plus space 1 end fraction almost equal to 4.38 semicolon end style

begin mathsize 14px style a subscript 3 space equals space fraction numerator 3 cubed over denominator square root of 27 space minus space 3 space plus space 1 end fraction almost equal to space 8.44 comma end style

begin mathsize 14px style S space almost equal to space 13.82. end style

Прыклад 6.16.

V. Праграма:

#include <iostream>

#include <cmath>

 

using namespace std;

 

int main()

{

  double eps, a;

  cout << "eps = ";

  cin >> eps;

  int n = 0;

  double s = 0;

  double d = 1;

  double f = 1;

  do  {

    n++;

    ///вылічэнне фактарыяла

    f *= n;

    ///узвядзенне 2 у ступень

    d *= 2;

    a =(n + d) / f;

    s += a;

  }

  while (abs(a) >= eps);

  cout << "summa= " << s << endl;

  return 0;

}

VI. Тэсціраванне

VII. Аналіз выніку. Паколькі фактарыял з’яўляецца функцыяй, якая надзвычай хутка расце, то элементы паслядоўнасці спадаюць.  Выпішам элементы:

begin mathsize 14px style a subscript 1 space equals space fraction numerator 1 space plus space 2 over denominator 1 end fraction space equals space 3 semicolon space space space space space a subscript 2 space equals space fraction numerator 2 space plus space 2 cubed over denominator 2 factorial end fraction space equals space 3 semicolon a subscript 3 space equals space fraction numerator 3 space plus space 2 cubed over denominator 3 factorial end fraction space equals 11 over 6 space almost equal to space 1 comma 83 semicolon a subscript 4 space equals space fraction numerator 4 space plus space 2 to the power of 4 over denominator 4 factorial end fraction space equals 20 over 24 space almost equal to space 0 comma 83 semicolon a subscript 5 space equals space fraction numerator 5 space plus space 2 to the power of 5 over denominator 5 factorial end fraction space equals 37 over 120 space almost equal to space 0 comma 31 semicolon a subscript 6 space equals space fraction numerator 6 space plus space 2 to the power of 6 over denominator 6 factorial end fraction space equals 70 over 720 space almost equal to space 0 comma 097. end style

Шосты элемент меншы за 0.1. Гэта апошняе складаемае ў суме. Сума першых шасці элементаў — ≈9.07.

Калі  eps = 0.01, да сумы, атрыманай для eps = 0.1, будуць дабаўляцца складаемыя, меншыя за  0.1, якія нязначна зменяць значэнне сумы.

.

Розніца ў значэннях сумы — ≈0.03. Чым меншая дакладнасць, тым менш будуць адрознівацца сумы.

6.5. Пабудова табліцы значэнняў функцыі

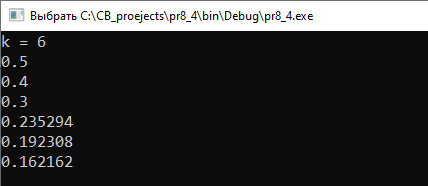
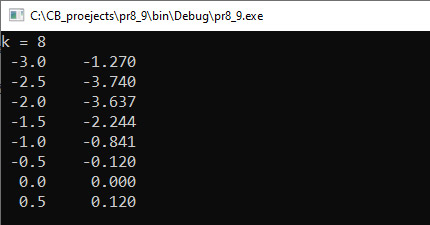
Прыклад 6.17. Вывесці на экран табліцу значэнняў функцыі y = x2sinx. Колькасць значэнняў уводзіцца. Пачатковае значэнне x = –3, значэнні аргумента выводзяцца з крокам h = 0.5.

Этапы выканання задання

I. Зыходныя данныя: k (колькасць пунктаў).

II. Вынік: k значэнняў аргумента і адпаведных ім значэнняў функцыі.

III. Алгарытм рашэння задачы.

1. Увод ліку k. 
2. Для атрымання табліцы трэба ў цыкле вылічваць і выводзіць значэнне аргумента і адпаведнае яму значэнне функцыі.

2.1. Пачатковае значэнне аргумента x = –3. Для атрымання чарговага значэння аргумента трэба да бягучага значэння прыбавіць крок h. 
2.2. Значэнне функцыі вылічваецца па формуле y = x2sinx. 
2.3. Атрыманыя значэнні выводзяцца на экран. Каб значэнні выводзіліся строга адно пад адным, трэба задаць фармат вываду ліку. Каманды, якія кіруюць фарматным вывадам, захоўваюцца ў бібліятэцы iomanip. З камандамі бібліятэкі можна пазнаёміцца ў Дадатку да главы 1.

3. Паколькі колькасць пунктаў вядомая, выкарыстаем цыкл  for.

IV. Апісанне пераменных: k – int, x, y, h – double.

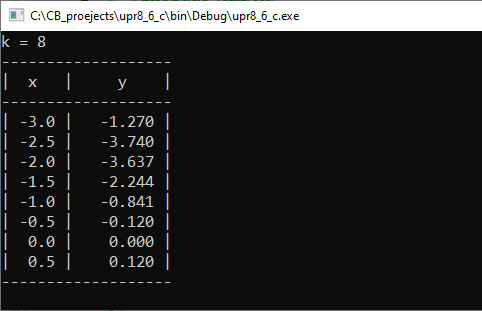
Прыклад 6.17.

V. Праграма:

#include<iostream>

#include<cmath>

#include<iomanip>

 

using namespace std;

 

int main()

{

  int k;

  cout << "k = ";

  cin >> k;

  double h = 0.5;

  double x = -3.;

  ///фіксаваць колькасць лічбаў

  cout << fixed;

  for (int n = 1; n <= k; n++) {

    double y = x * x * sin(x);

    ///памер поля для вываду

    cout.width(5);

    ///колькасць лічбаў пасля коскі

    cout.precision(1);

    cout << x;

    cout.width(10);

    cout.precision(3);

    cout << y << endl;

    x += h;

  }

  return 0;

}

VI. Тэсціраванне.

6.6. Вылучэнне лічбаў з ліку

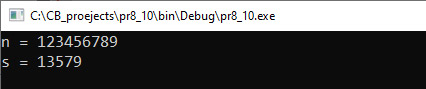
Прыклад 6.18. Дадзены натуральны лік n. Сфарміраваць новы лік, які складаецца з няцотных лічбаў ліку n.

Этапы выканання задання

I. Зыходныя даныя: n (лік).

II. Вынік: s (новы лік)

III. Алгарытм рашэння задачы.

1. Увод зыходных даных — лік n.
2. Вызначэнне пачатковага значэння новага ліку: s = 0.
3. У пераменнай r будзем захоўваць значэнне разраднай адзінкі для бягучай цотнай лічбы. Пачатковае значэнне r = 1.
4. У цыкле, пакуль у ліку ёсць лічбы:

4.1. Знайсці астачу от дзялення бягучага ліку на  10 (z — бягучая лічба ліку). 
4.2. Праверыць, ці з’яўляецца атрыманая лічба няцотнай. 
4.3. Калі лічба няцотная, то памножыць яе на значэнне разраднай адзінкі і прыбавіць да значэння s, павялічыць значэнне разраднай адзінкі ў 10 разоў. 
4.4. Паменшыць бягучы лік у 10 разоў.

5. Вывад значэння пераменнай s. Каліs = 0, то ў ліку няма няцотных лічбаў.

IV. Апісанне пераменных: n, s, r, z – int.

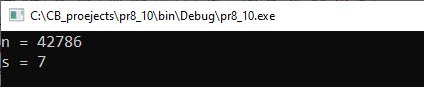
Прыклад 6.18.

V. Праграма:

#include <iostream>

 

using namespace std

 

int main()

{

  int n;

  cout << "n = ";

  cin >> n;

  int s = 0, r = 1;

  while (n > 0){

    int z = n % 10;

    if (z % 2) {

      s += z * r;

      r *= 10;

    }

    n /= 10;

  }

  if (s)

    cout << "s = " << s << endl;

  else

    cout << "net nechetnyh" << endl;

  return 0;

}

VI. Тэсціраванне.

6.7. Прасцейшае мадэліраванне

Прыклад 6.19. Рэзервуар напоўнены m літрамі воднага раствору, які змяшчае s кг цукру. Кожную мінуту забіраюць x літраў раствору і дабаўляюць y літраў вады. Канцэнтрацыя падтрымліваецца раўнамернай пры дапамозе памешвання. Колькі цукру будзе ў растворы праз k мінут?

Этапы выканання задання

I. Зыходныя даныя: числа m, s, x, k.

II. Вынік: s (новае значэнне)

 III. Алгарытм рашэння задачы.

1. Увод зыходных даных. 
2. У пераменнай с будзем захоўваць значэнне бягучай канцэнтрацыі раствору, у пераменнай v — колькасць вады. 
3. У цыкле ад 1 да k:

3.1. Памяншаем колькасць раствору на x. 
3.2. Дабаўляем ваду. 
3.3. Пералічваем канцэнтрацыю раствору. 
3.4. Калі ў нейкі момант увесь раствор вылілі, то перарываем цыкл.

4. Вывад значэння пераменнай s. Калі колькасць раствору меншая або роўная нулю, то выводзім паведамленне «цукру не засталося», інакш выводзім колькасць цукру, якая засталася.

IV. Апісанне пераменных: n, s, r, z — int.

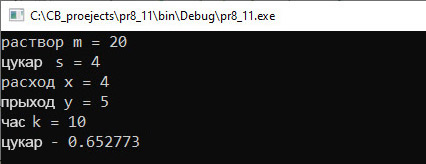
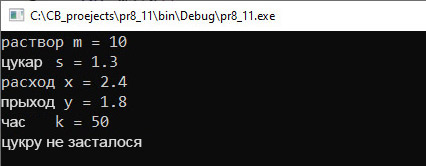
Прыклад 6.19.

V. Праграма:

#include <iostream>

 

using namespace std;

 

int main()

{

  setlocale(0,"");

  double m, s, x, y;

  cout << "раствор m = ";

  cin >> m;

  cout << "цукар s = ";

  cin >> s;

  cout << "расход x = ";

  cin >> x;

  cout << "прыход y = ";

  cin >> y;

  int k;

  cout << "час k = ";

  cin >> k;

  double c = s / m;

  for (int i = 0; i < k; i++){

    m -= x;

    if (m <= 0) break;

    s = c * m;

    m += y;

    c = s / m;

  }

  if (m <= 0)

    cout << "цукру не засталося" << endl;

  else

    cout << "цукру - " << s << endl;

  return 0;

}

 VI.  Тэсціраванне.

Практыкаванні

    

1. Напішыце праграму для вылічэння першых n элементаў паслядоўнасці Фібаначы.

1. Для якога максімальнага значэння n праграма выдае карэктны адказ?
2. Змяніце праграму так, каб яна выводзіла значэнне ліку Фібаначы па ўведзеным нумары.
3. Замяніце ў праграме тып int на тып long long. Якое максімальнае значэнне n можна ўвесці зараз?

2. Напішыце праграму, якая будзе выводзіць на экран элементы паслядоўнасці трыбаначы — першыя элементы паслядоўнасці: 0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149… . Кожны элемент, пачынаючы з чацвёртага, роўны суме трох папярэдніх: an = an – 1 +  an – 2 + an – 3.

1. Па зададзеным n вывесці элемент паслядоўнасці.
2. Для зададзенага x вывесці элементы паслядоўнасці, меншыя x.

3. Напішыце праграму, якая знойдзе першы адмоўны элемент паслядоўнасці sin(tgn)n = 1, 2, ... і яго нумар.

4. Выканайце заданні для прыкладу 6.15.

1. Замяніце ў рашэнні задачы цыкл  for на цыкл while або do…while.
2. Ваня вырашыў скараціць колькасць радкоў у праграме і запісаў цыкл наступным чынам:

    for (int n = 1; n <= m; n++){

      double a = n * n * n / (sqrt(n * n * n)- n + 1);

      s += a;

    }

Чаму для  m = 2000 Ваня атрымаў у адказе  s = nan?

5. Напішыце праграму, якая знойдзе суму першых m элементаў паслядоўнасці. Лік m уводзіцца. Элементы паслядоўнасці задаюцца формулай.

begin mathsize 16px style 1. space a subscript n space equals space 1 over n cubed. 2. space a subscript n space equals space fraction numerator 2 cos n over denominator left parenthesis n space plus space 1 right parenthesis squared end fraction. 3. space a subscript n space equals space fraction numerator square root of n cubed end root over denominator n squared space plus space n space plus space 3 end fraction. 4. space a subscript n space equals space fraction numerator fourth root of n space plus space 3 end root over denominator n cubed space plus space 4 n end fraction. end style

6. Напісаць праграму для вылічэння сумы, якая мае сваімі складаемымі элементы паслядоўнасці a subscript n. Вылічэнні выконваць да таго часу, пакуль не знойдзецца складаемае, для якога правільная няроўнасць open vertical bar a subscript n close vertical bar space less than space e p s. Значэнне eps уводзіцца (0 < eps < 1 ).

begin mathsize 16px style 1. space a subscript n space equals space fraction numerator 2 to the power of n space plus space n over denominator 5 to the power of n end fraction. 2. space a subscript n space equals space fraction numerator 3 to the power of n over denominator n factorial space plus space 2 end fraction. 3. space a subscript n space equals left parenthesis – 1 right parenthesis to the power of n space fraction numerator 3 to the power of n space plus space 1 over denominator n factorial space plus space 5 end fraction. 4. space a subscript n space equals space 2 over 3 to the power of n space plus space fraction numerator 2 over denominator n factorial end fraction. end style

7. Напішыце праграму, якая знойдзе здабытак з n сумножнікаў наступнага выгляду. Значэнне n уводзіцца.

1. space open parentheses 1 space plus space 1 over 1 squared close parentheses open parentheses 1 space plus space 1 over 2 squared close parentheses open parentheses 1 space plus space 1 over 3 squared close parentheses... open parentheses 1 space plus space 1 over n squared close parentheses. 2. space a open parentheses a space plus 1 close parentheses... open parentheses a space plus space n space – 1 close parentheses. space Лік space а space ўводзіцца. 3. space open parentheses space 1 space minus space 1 over 1 squared close parentheses open parentheses 1 space minus space 1 over 2 cubed close parentheses open parentheses 1 space minus space 1 over 2 to the power of 4 close parentheses... open parentheses 1 space minus space 1 over 2 to the power of straight n space plus 1 end exponent close parentheses. 4. space open parentheses x space plus space 2 x squared space plus x cubed close parentheses left parenthesis straight x squared space plus space 2 straight x cubed space plus straight x to the power of 4 right parenthesis left parenthesis straight x cubed space plus space 2 straight x to the power of 4 space plus straight x to the power of 5 right parenthesis... left parenthesis straight x to the power of n space plus space 2 straight x to the power of n italic space plus space 1 end exponent space plus straight x to the power of n space plus space 2 end exponent right parenthesis. Лік space х space space уводзіцца.

8. Выканайце заданне для прыкладу 6.17.

    1. Замяніце ў рашэнні задачы цыкл for на цыкл while або  do…while.
    2.  Атрымайце табліцу значэнняў функцыі на адрэзку [–3; 3]. У якасці ўмовы ў цыкле можна выкарыстоўваць наступнае: x < = 3;
    3. Дабаўце ў праграму вывад меж вакол табліцы:

9. Напішыце праграму, якая пабудуе табліцы значэнняў для наступных функцый.

1. space y space equals space x squared space – space 5 x space – space 3 comma space x element of space open square brackets – 3 semicolon space 3 close square brackets comma space уводзіцца space значэнне space кроку space h. 2. space y space equals cos space x space – space x squared comma space space x element of space open square brackets – straight pi semicolon space straight pi close square brackets comma space space уводзіцца space колькасць space пунктаў. 3. space y space equals 2 space plus space fraction numerator 3 x minus 7 over denominator x squared space plus space 1 end fraction comma space space x element of space open square brackets a italic comma italic space b close square brackets to the power of left square bracket 1 right square bracket end exponent comma space space уводзяцца space значэнні space space а comma space b space straight і space колькасць space пунктаў. 4. space y space equals 2 space plus space 1 over x sin x comma space space x element of space open square brackets a italic comma italic space b close square brackets comma space у водзяцца space значэнні space space a comma space b space straight і space колькасць space пунктаў. space Неабходна space ўлічыць space вобласць space вызначэння space функцыі.

10. Праграму з прыкладу 6.18 змянілі. Сфармулюйце задачу, якая рашаецца з  дапамогай дадзенай праграмы.

#include<iostream>

 

using namespace std;

 

int main()

{

  int i, n;

  cout << "n = ";

  cin >> n;

  cout << "i = ";

  cin >> i;

  int k = 0;

  while (n > 0)

  {

    int z = n % 10; //бягучая лічба

    k++;

    if (k == i){

      cout << "v razrjade " << i;

      cout << " stoit zifra "<< z << endl;

    }

  n /= 10; //памяншэнне ліку ў 10 разоў

  }

  if (i > k){

    cout << "v chisle "<<k<<" cifr, ";

    cout << "v razrjade " << i << " net cifr " << endl;

  }

  else

  cout<<"v chisle "<<k<<" cifr";

  return 0;

}

11. Дадзены натуральны лік n. Напішыце праграму, якая вызначыць, якіх лічбаў у ліку больш, цотных ці няцотных.

12. Дадзены натуральны лік n. Напішыце праграму, якая выведзе нумары разрадаў, у якіх стаяць лічбы, кратныя 3, ці паведамленне, што такіх лічбаў няма.

13. Напішыце праграму, якая выведзе на экран лічбу, што стаіць на сярэдняй пазіцыі ліку, калі лік мае няцотную колькасць лічбаў, ці 2 сярэднія для ліку з цотнай колькасцю лічбаў.

14. Напішыце праграму, якая пасля кожнай лічбы 1 у ліку ўставіць яшчэ адну адзінку. Напрыклад, из 51214  → 5112114.

15. Выканайце заданне для прыкладу 6.19.

1. Для сітуацыі, калі цукар заканчваецца, выведзіце значэнне часу, калі гэта адбылося.
2. Змяніце праграму так, каб задавалася пачатковая і канчатковая колькасць цукру, а разлічваўся час, неабходны для такога змянення канцэнтрацыі. 
3. Змяніце праграму так, каб па ўведзеным часе і колькасці цукру ў пачатку і ў канцы працэсу разлічваўся пачатковы аб’ём раствору.


[1] Падказка: begin mathsize 14px style h space equals space fraction numerator b space – space a over denominator k space – space 1 end fraction. end style