§ 30. Сіла Лорэнца. Рух зараджаных часціц у магнітным полі

Сайт:	Профильное обучение
Курс:	Фізіка. 10 клас
Книга:	§ 30. Сіла Лорэнца. Рух зараджаных часціц у магнітным полі
Напечатано::	Гость
Дата:	Воскресенье, 28 Апрель 2024, 19:10

Паколькі электрычны ток уяўляе з сябе ўпарадкаваны рух зараджаных часціц, то гэта азначае, што магнітнае поле, дзейнічаючы на праваднік з токам, дзейнічае тым самым на кожную з гэтых часціц. Такім чынам, сілу Ампера можна разглядаць як вынік складання сіл, што дзейнічаюць на асобныя зараджаныя часціцы, якія рухаюцца. Як можна вызначыць сілу, што дзейнічае з боку магнітнага поля на зараджаную часціцу, якая рухаецца ў гэтым полі?

Сіла Лорэнца. Сілу, якой магнітнае поле дзейнічае на зараджаную часціцу, што рухаецца ў гэтым полі, называюць сілай Лорэнца ў гонар выдатнага нідэрландскага фізіка Хендрыка Антона Лорэнца (1853–1928).

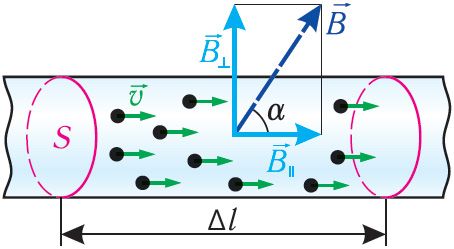
Модуль сілы Лорэнца можна вызначыць па формуле $F subscript straight Л equals F subscript straight А over N$ , дзе N — агульная колькасць свабодных зараджаных аднолькавых часціц на прамалінейным участку правадніка даўжынёй Δl (мал. 167). Калі модуль зараду адной часціцы q, а модуль сумарнага зараду ўсіх часціц Nq, то згодна з азначэннем сілы току $begin mathsize 18px style I equals fraction numerator N q over denominator increment t end fraction end style$ , дзе Δt — прамежак часу, за які зараджаная часціца праходзіць участак правадніка даўжынёй Δl. Тады

$begin mathsize 18px style F subscript straight Л equals fraction numerator B I increment l sin straight alpha over denominator N end fraction equals fraction numerator B N q increment l sin straight alpha over denominator increment t N end fraction equals fraction numerator B q increment l sin straight alpha over denominator increment t end fraction. end style$

Паколькі $begin mathsize 18px style fraction numerator increment l over denominator increment t end fraction equals upsilon end style$ — модуль сярэдняй скорасці ўпарадкаванага руху зараджанай часціцы ў стацыянарным^* электрычным полі ўнутры правадніка, то формулу для вызначэння модуля сілы Лорэнца можна запісаць у выглядзе:

$begin mathsize 18px style F subscript straight Л equals B q upsilon sin straight alpha comma end style$

(30.1)

дзе α — вугал паміж напрамкамі індукцыі магнітнага поля $begin mathsize 18px style B with rightwards arrow on top end style$ і скорасці $begin mathsize 18px style upsilon with rightwards arrow on top end style$ упарадкаванага руху зараджанай часціцы.

З формулы (30.1) вынікае, што сіла Лорэнца максі мальная ў выпадку, калі зараджаная часціца рухаецца перпендыкулярна напрамку індукцыі магнітнага поля (α = 90°). Калі часціца рухаецца ўздоўж лініі індукцыі поля (α = 0° або α = 180°), сіла Лорэнца на яе не дзейнічае. Сіла Лорэнца залежыць ад выбару інерцыяльнай сістэмы адліку, бо ў розных сістэмах адліку скорасць руху зараджанай часціцы можа адрознівацца.

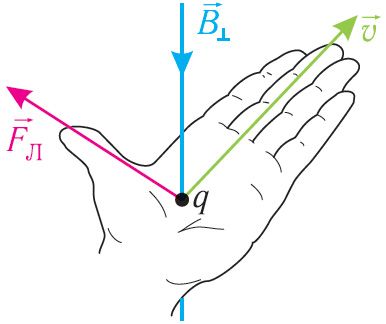
Напрамак сілы Лорэнца, якая дзейнічае на зараджаную часціцу, як і напрамак сілы Ампера, вызначаюць паводле правіла левай рукі (мал. 168): калі левую руку размясціць так, каб складнік індукцыі магнітнага поля, перпендыкулярны скорасці руху часціцы, уваходзіў у далонь, а чатыры пальцы былі накіраваныя па руху дадатна зараджанай часціцы (супраць руху адмоўна зараджанай часціцы), то адагнуты на 90° у плоскасці далоні вялікі палец пакажа напрамак сілы Лорэнца, якая дзейнічае на часціцу.

Сіла Лорэнца перпендыкулярная як напрамку скорасці $begin mathsize 18px style upsilon with rightwards arrow on top end style$ руху часціцы, так і напрамку індукцыі $begin mathsize 18px style B with rightwards arrow on top end style$ магнітнага поля.

Ад тэорыі да практыкі

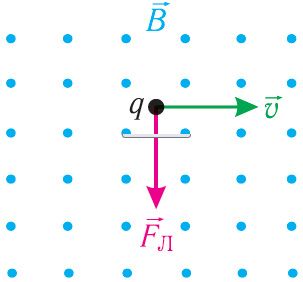
На малюнку 169 паказаны напрамкі індукцыі $begin mathsize 18px style B with rightwards arrow on top end style$ магнітнага поля, скорасці $begin mathsize 18px style upsilon with rightwards arrow on top end style$ руху часціцы ў дадзены момант часу і сілы Лорэнца $begin mathsize 18px style F with rightwards arrow on top subscript straight Л end style$ , якая дзейнічае на часціцу з боку магнітнага поля. Вызначце знак зараду часціцы.

* Электрычнае поле, якое ствараецца і падтрымліваецца крыніцай току на працягу доўгага прамежку часу і забяспечвае пастаянны электрычны ток у правадніку, называюць стацыянарным электрычным полем. ↑

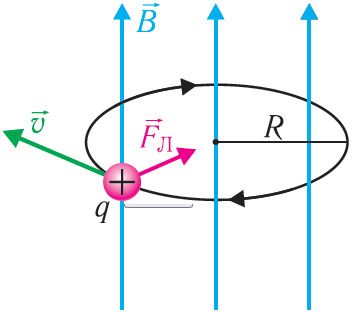
Рух зараджаных часціц у аднародным магнітным полі. Пад дзеяннем сілы Лорэнца часціцы, якія маюць электрычны зарад, рухаюцца ў магнітным полі па крывалінейных траекторыях. Прычым калі ў дадзенай інерцыяльнай сістэме адліку напрамак скорасці руху часціцы перпендыкулярны напрамку індукцыі аднароднага магнітнага поля ( $begin mathsize 18px style upsilon with rightwards arrow on top perpendicular B with rightwards arrow on top end style$ , $begin mathsize 18px style straight alpha equals 90 degree end style$ ), то траекторыяй руху зараджанай часціцы з’яўляецца акружнасць (мал. 170).

Няхай у аднародным магнітным полі, індукцыя якога $begin mathsize 18px style B with rightwards arrow on top end style$ , рухаецца часціца са скорасцю $begin mathsize 18px style upsilon with rightwards arrow on top end style$ , накіраванай перпендыкулярна лініям індукцыі. Маса часціцы m і зарад q. Паколькі сіла Лорэнца $begin mathsize 18px style F with rightwards arrow on top subscript straight Л end style$ перпендыкулярная скорасці $begin mathsize 18px style upsilon with rightwards arrow on top end style$ руху часціцы (гл. мал. 170), то гэтая сіла змяняе толькі напрамак скорасці, надаючы часціцы цэнтраімклівае паскарэнне, модуль якога згодна з другім законам Ньютана:

$begin mathsize 18px style alpha equals F subscript straight Л over m equals fraction numerator B q upsilon over denominator m end fraction. end style$

У выніку часціца рухаецца па акружнасці, радыус якой можна вызначыць з формулы $begin mathsize 18px style alpha equals upsilon squared over R end style$ :

$begin mathsize 18px style R equals upsilon squared over alpha equals fraction numerator upsilon squared m over denominator B q upsilon end fraction equals fraction numerator m upsilon over denominator B q end fraction. end style$

Перыяд Т абарачэння часціцы, якая рухаецца па акружнасці ў аднародным магнітным полі:

$begin mathsize 18px style T equals fraction numerator 2 straight pi R over denominator upsilon end fraction equals fraction numerator 2 straight pi over denominator upsilon end fraction times fraction numerator m upsilon over denominator B q end fraction equals fraction numerator 2 straight pi m over denominator B q end fraction. end style$

(30.2)

Як вынікае з выразу (30.2), перыяд абарачэння часціцы не залежыць ад модуля скорасці яе руху і радыуса траекторыі, а вызначаецца толькі модулем зараду часціцы, яе масай і значэннем індукцыі магнітнага поля.

Ад тэорыі да практыкі

У аднародным магнітным полі, модуль індукцыі якога В = 4,0 мТл, перпендыкулярна лініям індукцыі поля рухаецца электрон. Чаму роўны модуль паскарэння электрона, калі модуль скорасці яго руху $begin mathsize 18px style upsilon equals 2 comma 5 times 10 to the power of 6 space straight м over straight с end style$ ? Маса і модуль зараду электрона m_е = 9,1 · 10^–31 кг і е = 1,6 · 10^–19 Кл адпаведна.

Адсылка да электроннага дадатку для павышанага ўзроўню

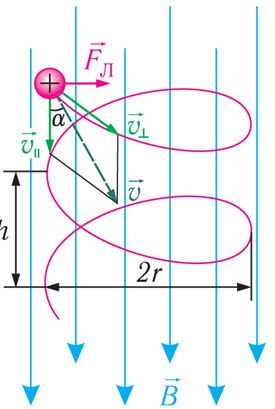
Калі зараджаная часціца рухаецца ў аднародным магнітным полі так, што напрамак яе скорасці $begin mathsize 18px style upsilon with rightwards arrow on top end style$ утварае з напрамкам індукцыі магнітнага поля $B with rightwards arrow on top$ вугал α, прычым α ≠ 0, α ≠ π, то траекторыя руху часціцы ўяўляе з сябе спіральную лінію (мал. 170.1). Пры гэтым радыус R спіральнай лініі залежыць ад модуля складніка скорасці, перпендыкулярнага індукцыі магнітнага поля, а крок спіральнай лініі h — ад модуля складніка скорасці υ_||, паралельнага магнітнай індукцыі. Такім чынам, траекторыя руху зараджанай часціцы нібы навіваецца на лініі магнітнай індукцыі.

Падобная з'ява адбываецца ў магнітным полі Зямлі, якое ахоўвае ўсё жывое ад патокаў зараджаных часціц з касмічнай прасторы. Зараджаныя часціцы з космасу, якія рухаюцца з вялізнымі скарасцямі, захопліваюцца магнітным полем Зямлі і ўтвараюць так званыя радыяцыйныя паясы (мал. 170.2), у якіх часціцы перамяшчаюцца па спіралепадобных траекторыях паміж паўночным і паўднёвым магнітнымі полюсамі туды і назад за прамежак часу, роўны прыкладна долям секунды. Толькі ў палярных абласцях некаторая частка часціц урываецца ў верхнія слаі атмасферы, выклікаючы палярныя ззянні (мал. 170.3).

Калі зараджаная часціца ў момант узнікнення знешняга электрычнага поля знаходзілася ў спакоі, то $fraction numerator m v squared over denominator 2 end fraction equals q U$ , дзе U — напружанне паміж пунктамі, у якіх знаходзілася часціца ў моманты ўзнікнення знешняга электрычнага поля і выхаду з яго, q — модуль зараду часціцы. Таму модуль скорасці часціцы пры выхадзе з электрычнага поля:

$v equals square root of fraction numerator 2 q U over denominator m end fraction end root.$

Калі пасля гэтага часціца трапляе ў аднароднае магнітнае поле, індукцыя $B with rightwards arrow on top$ якога перпендыкулярная напрамку яе скорасці, то радыус акружнасці, па дузе якой будзе рухацца часціца, $R equals fraction numerator m v over denominator B q end fraction$ , адкуль

$q over m equals fraction numerator 2 U over denominator R squared B squared end fraction.$

Велічыню $q over m$ называюць удзельным зарадам часціцы. Таму калі доследным шляхам вызначыць радыус траекторыі руху часціцы ў магнітным полі, то, ведаючы індукцыю магнітнага поля і паскаральнае напружанне электрычнага поля, можна разлічыць удзельны зарад часціцы. Гэты метад выкарыстоўваюць пры канструяванні прыбораў, якія называюць мас-спектрометрамі.

Цікава ведаць

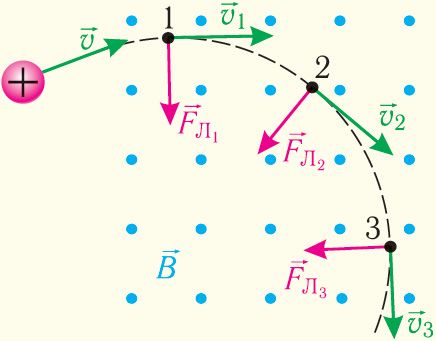
Паколькі сіла Лорэнца накіравана пад вуглом 90° да скорасці руху зараджанай часціцы ў кожным пункце траекторыі (мал. 171), то работа гэтай сілы пры руху зараджанай часціцы ў магнітным полі роўная нулю. Таму кінетычная энергія часціцы, якая рухаецца ў стацыянарным (нязменным у часе) магнітным полі, не змяняецца, гэта значыць стацыянарнае магнітнае поле нельга выкарыстоўваць для паскарэння зараджаных часціц.

Павелічэнне кінетычнай энергіі часціцы, гэта значыць яе разгон, магчыма пад дзеяннем электрычнага поля (у гэтым выпадку змена кінетычнай энергіі часціцы роўная рабоце сілы поля). Таму ў сучасных паскаральніках (мал. 172) зараджаных часціц электрычнае поле выкарыстоўваюць для паскарэння, а магнітнае — для «фарміравання» траекторыі руху зараджаных часціц.

1. Як вызначаюць модуль сілы, што дзейнічае з боку магнітнага поля на зараджаную часціцу, якая ў ім рухаецца?

2. Як вызначаюць напрамак сілы Лорэнца?

3. Зараджаная часціца рухаецца ў аднародным магнітным полі са скорасцю, накіраванай перпендыкулярна лініям індукцыі. Па якой траекторыі рухаецца часціца?

4. Ад чаго залежыць перыяд абарачэння зараджанай часціцы ў аднародным магнітным полі?

Адсылка да электроннага дадатку для павышанага ўзроўню

5. Чаму сіла Лорэнца змяняе напрамак скорасці руху часціцы, але не ўплывае на яе модуль?

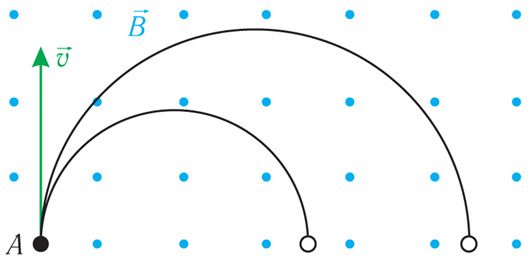
6. На малюнку 172.1 паказаны траекторыі руху дзвюх часціц, якія маюць аднолькавыя зарады. Часціцы ўлятаюць у аднароднае магнітнае поле з аднаго пункта А з аднолькавымі скарасцямі. Вызначце знак зараду часціц. Растлумачце прычыну несупадзення траекторый іх руху.

Прыклады рашэння задачы

Прыклад 1. Электрон рухаецца ў аднародным магнітным полі па акружнасці радыусам R = 12 см са скорасцю, модуль якой значна меншы за модуль скорасці святла. Вызначце модуль імпульсу электрона, калі модуль індукцыі магнітнага поля В = 0,020 Тл.

Дадзена:
R = 12 см = 0,12 м
В = 0,020 Тл

р — ?

Рашэнне. Згодна з азначэннем модуль імпульсу электрона p = mv, дзе m — маса электрона; v — модуль скорасці яго руху.

На электрон у магнітным полі дзейнічаюць сіла Лорэнца і сіла цяжару, модуль якой у шмат разоў меншы за модуль сілы Лорэнца. Таму дзеянне сілы цяжару на зараджа ную часціцу, якая рухаецца ў магнітным полі, можна не прымаць пад увагу. Згодна з другім законам Ньютана $begin mathsize 18px style fraction numerator m upsilon squared over denominator R end fraction equals B e upsilon end style$ , адкуль $begin mathsize 18px style upsilon equals fraction numerator B e R over denominator m end fraction end style$ , дзе е = 1,6 · 10^–19 Кл — модуль зараду электрона.

Значыць, $begin mathsize 18px style p equals m fraction numerator B e R over denominator m end fraction equals B e R end style$ .

$begin mathsize 18px style p equals 0 comma 020 space Тл times 1 comma 6 times 10 to the power of negative 19 end exponent space Кл times 0 comma 12 space straight м space equals 3 comma 8 times 10 to the power of negative 22 end exponent space fraction numerator кг times straight м over denominator straight с end fraction. end style$

Адказ: $begin mathsize 18px style p equals 3 comma 8 times 10 to the power of negative 22 end exponent space fraction numerator кг times straight м over denominator straight с end fraction end style$ .

Адсылка да электроннага дадатку для павышанага ўзроўню

Прыклад 2. Электрон, паскораны са стану спакою ў электрастатычным полі рознасцю патэнцыялаў U = 270 В, рухаецца паралельна тонкаму доўгаму прамалінейнаму правадніку, які знаходзіцца ў вакууме, на адлегласці r = 5,0 мм ад яго. Вызначце модуль сілы, якая пачне дзейнічаць на электрон, калі па правадніку пусціць электрычны ток, а таксама радыус крывізны яго траекторыі ў пачатку скрыўленага ўчастка пры сіле току ў правадніку I = 10 А.

Дадзена:
U = 270 В
r = 5,0 мм = 5,0 · 10^–3 м
I = 10 А

F_л — ?
R — ?

Рашэнне. Модуль скорасці руху электрона, паскоранага са стану спакою ў электрастатычным полі рознасцю патэнцыялаў U, можна вызначыць, выкарыстаўшы формулу (2) $v equals square root of fraction numerator 2 e U over denominator m end fraction end root$ . Модуль індукцыі магнітнага поля, створанага тонкім доўгім прамалінейным правадніком, калі па ім прапусціць электрычны ток I: $B equals fraction numerator straight mu subscript 0 I over denominator 2 straight pi r end fraction$ .

Тады, выкарыстаўшы формулу (1), можна вызначыць модуль сілы Лорэнца:

$F subscript straight л equals e fraction numerator straight mu subscript 0 I over denominator 2 straight pi r end fraction times square root of fraction numerator 2 e U over denominator m end fraction. end root$

$F subscript straight л equals 1 comma 6 times 10 to the power of negative 19 end exponent space Кл space times 4 times 3 comma 14 times 10 to the power of negative 7 end exponent space straight Н over straight А squared space times fraction numerator 10 space straight А over denominator 2 times 3 comma 14 times 5 comma 0 times 10 to the power of negative 3 end exponent space straight м end fraction times square root of fraction numerator 2 times 1 comma 6 times 10 to the power of negative 19 end exponent space Кл space times 270 space straight В over denominator 9 comma 1 times 10 to the power of negative 31 end exponent space кг end fraction end root equals 6 comma 2 times 10 to the power of negative 16 end exponent space straight Н.$

Як толькі з'яўляецца магнітнае поле, якое ствараецца правадніком з токам, на электрон пачынае дзейнічаць сіла Лорэнца, і электрон працягвае рухацца, але ўжо з цэнтраімклівым паскарэннем: $F with rightwards arrow on top subscript straight л equals m a with rightwards arrow on top$ . Тады

$F subscript straight л equals m v squared over R$ , адкуль $R equals fraction numerator m v squared over denominator F subscript straight л end fraction equals fraction numerator 2 e U over denominator F subscript straight л end fraction$ .

$R equals fraction numerator 2 times 1 comma 6 times 10 to the power of negative 19 end exponent space Кл space times 270 space straight В over denominator 6 comma 2 times 10 to the power of negative 16 end exponent space straight Н end fraction equals 0 comma 14 space straight м.$

Адказ: F_л = 6,2 · 10⁻¹⁶ Н, R = 0,14 м.

Практыкаванне 22

1. Электрон рухаецца са скорасцю, модуль якой $begin mathsize 18px style upsilon equals 2 comma 0 times 10 to the power of 8 space см over straight с end style$ , перпендыкулярна лініям індукцыі аднароднага магнітнага поля, модуль індукцыі якога В = 1,6 мТл. Вызначце модуль сілы, якая дзейнічае на электрон у магнітным полі.

2. Электрон рухаецца ў аднародным магнітным полі па акружнасці, радыус якой R = 8,0 мм. Вызначце модуль індукцыі магнітнага поля, калі модуль скорасці руху электрона $begin mathsize 18px style upsilon equals 4 comma 0 times 10 to the power of 6 space см over straight с end style$ . Маса электрона m_е = 9,1 · 10^–31 кг.

3. Пылінка рухаецца ў аднародным магнітным полі, модуль індукцыі якога В = 1,0 Тл, перпендыкулярна лініям індукцыі. Маса і зарад пылінкі m = 0,80 мг і q = 1,6 нКл адпаведна. Вызначце перыяд абарачэння пылінкі.

4. Электрон рухаецца ў аднародным магнітным полі, модуль індукцыі якога В = 2,0 мТл, па акружнасці радыусам R = 2,0 см. Вызначце кінетычную энергію электрона. Маса электрона m_е = 9,1 · 10^–31 кг.

5. Вызначце, якую паскаральную рознасць патэнцыялаў павінна прайсці са стану спакою часціца, каб у аднародным магнітным полі, модуль індукцыі якога В = 80 мТл, на яе дзейнічала сіла Лорэнца, модуль якой F = 20 мкН. Маса часціцы m = 12 мг, яе зарад Q = 3,0 мкКл. У магнітнае поле часціца ўлятае перпендыкулярна лініям індукцыі.

Адсылка да электроннага дадатку для павышанага ўзроўню

6. У аднароднае магнітнае поле ўлятаюць часціцы з зарадамі, модулі якіх аднолькавыя (мал. 172.2). Выберыце два праўдзівыя сцвярджэнні.

1) Траекторыя 1 належыць адмоўна зараджанай часціцы з найменшай кінетычнай энергіяй.

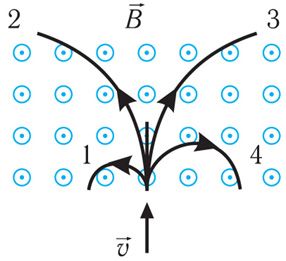
2) Траекторыя 2 належыць дадатна зараджанай часціцы з найменшай кінетычнай энергіяй.

3) Траекторыя 3 належыць дадатна зараджанай часціцы з найбольшай кінетычнай энергіяй.

4) Траекторыя 4 належыць адмоўна зараджанай часціцы з найбольшай кінетычнай энергіяй.

5) Знакі зарадаў усіх часціц аднолькавыя.

7. Зараджаная часціца рухаецца ў прасторы з аднароднымі электрычным і магнітным палямі, лініі напружанасці і магнітнай індукцыі якіх узаемна перпендыкулярныя. Модулі напружанасці электрычнага поля і індукцыі магнітнага адпаведна Е = 0,24 $кВ over straight м$ і В = 0,04 Тл. Вызначце модуль скорасці раўнамернага руху зараджанай часціцы. Дзеянне сілы цяжару на часціцу не прымайце пад увагу.

§ 30. Сіла Лорэнца. Рух зараджаных часціц у магнітным полі

Оглавление