§ 24. Энергія электрастатычнага поля кандэнсатара
| Сайт: | Профильное обучение |
| Курс: | Фізіка. 10 клас |
| Книга: | § 24. Энергія электрастатычнага поля кандэнсатара |
| Напечатано:: | Гость |
| Дата: | Воскресенье, 6 Июль 2025, 09:00 |
Працэс зарадкі кандэнсатара можна ўявіць як перанос зараду q з адной абкладкі на другую, у выніку чаго адна з іх набывае зарад –q, а другая — +q. Работа, выкананая пры гэтым знешняй сілай, роўная энергіі электрастатычнага поля зараджанага кандэнсатара.
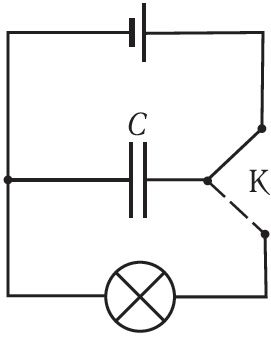
Пераканацца ў тым, што зараджаны кандэнсатар валодае энергіяй, можна з дапамогай доследу. Збяром электрычны ланцуг, які складаецца з крыніцы току, кандэнсатара і электрычнай лямпы. Схема ланцуга прыведзена на малюнку 125. Зарадзім кандэнсатар, далучыўшы яго да крыніцы току. Затым адключым кандэнсатар ад крыніцы току і падключым яго да лямпы. Пры гэтым назіраем кароткачасовую ўспышку святла. У дадзеным выпадку падчас разрадкі кандэнсатара энергія, назапашаная ім пры зарадцы, ператвараецца ва ўнутраную энергію спіралі лямпы, частка гэтай энергіі расходуецца на выпраменьванне святла. У час праходжання электрычнага току па ланцугу з крыніцай току кандэнсатар зараджаўся, гэта значыць на яго абкладках назапашваліся электрычныя зарады. Пры гэтым паміж абкладкамі кандэнсатара і ў прасторы вакол яго ўзнікла электрастатычнае поле. Сумарны электрычны зарад абедзвюх абкладак кандэнсатара да яго зарадкі, падчас зарадкі і пасля разрадкі роўны нулю. Адзіная змена, якая адбылася пры разрадцы кандэнсатара, заключаецца ў тым, што знікла электрастатычнае поле, якое стваралася зарадамі абедзвюх абкладак кандэнсатара. Такім чынам, энергіяй валодала электрастатычнае поле, утворанае зарадамі абкладак зараджанага кандэнсатара.
![]()
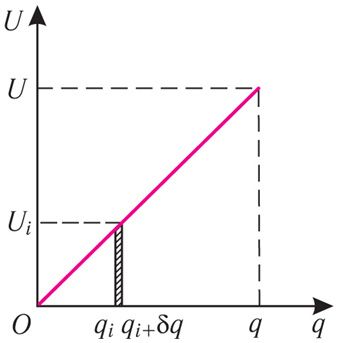
Калі форма і памеры абкладак кандэнсатара, а таксама адлегласць паміж імі і дыэлектрычныя ўласцівасці асяроддзя, якое запаўняе прастору паміж абкладкамі, застаюцца нязменнымі, то напружанне на кандэнсатары прама прапарцыянальнае модулю зараду яго абкладак (мал. 125.1). Каб павялічыць модуль зараду на абкладках ад qi да qi + δq, знешняй сіле неабходна выканаць работу
па перамяшчэнні бясконца малой дадатнай порцыі зараду δq з адмоўнай абкладкі на дадатную. Гэтай рабоце на малюнку 125.1 адпавядае плошча заштрыхаванага слупка. Поўная ж работа Азнеш па зарадцы кандэнсатара да напружання U роўная суме плошчаў усіх аналагічных слупкоў, гэта значыць плошчы фігуры пад графікам залежнасці U(q). У дадзеным выпадку — плошчы трохвугольніка, роўнай палове здабытку яго асновы на вышыню:
Прырашчэнне энергіі электрастатычнага поля зараджанага кандэнсатара роўнае рабоце, выкананай знешняй сілай пры яго зарадцы:
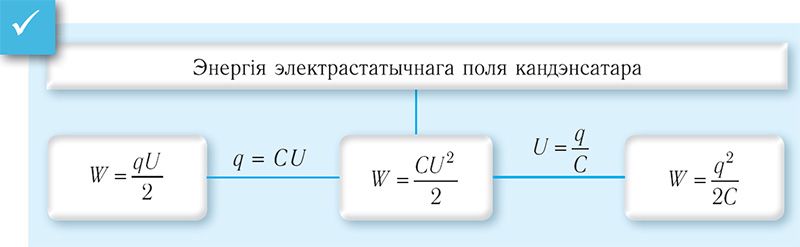
Улічваючы, што q = CU, формулу для вызначэння энергіі электрастатычнага поля зараджанага кандэнсатара можна запісаць у выглядзе:
, або
.
Энергію электрастатычнага поля зараджанага плоскага кандэнсатара можна выразіць праз напружанасць поля, сканцэнтраванага паміж яго абкладкамі (мал. 125.2). Электраёмістасць плоскага кандэнсатара
, напружанне паміж абкладкамі U = Ed. Такім чынам,
дзе V = Sd — аб’ём прасторы паміж абкладкамі кандэнсатара.
Як зменіцца энергія электрастатычнага поля зараджанага кандэнсатара пры павелічэнні адлегласці паміж яго абкладкамі, калі: а) кандэнсатар адключаны ад крыніцы току; б) кандэнсатар падключаны да крыніцы току?
Прымяненне кандэнсатараў. Кандэнсатары знаходзяць шырокае прымяненне ў электратэхніцы, радыётэхнічнай і тэлевізійнай апаратуры, радыёлакацыйнай тэхніцы, тэлефаніі, тэхніцы лічыльнарашальных прылад, лазернай тэхніцы, электраэнергетыцы (напрыклад, для паляпшэння каэфіцыента магутнасці прамысловых установак, рэгулявання напружання ў размеркавальных сетках, у прыладах асвятлення люмінесцэнтнымі лямпамі), металапрамысловасці (напрыклад, для плаўкі і тэрмічнай апрацоўкі металаў), здабыўной прамысловасці (напрыклад, у электравыбуховых прыладах), медыцынскай тэхніцы (напрыклад, у рэнтгенаўскай апаратуры, прыборах электратэрапіі), фотатэхніцы (для атрымання ўспышкі святла пры фатаграфаванні).
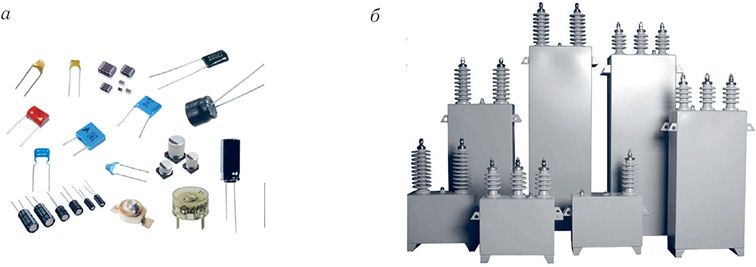
У сувязі з гэтым разам з мініяцюрнымі кандэнсатарамі (мал. 126, а), якія маюць масу менш як грам і памеры каля некалькіх міліметраў, існуюць кандэнсатары з масай у некалькі тон (мал. 126, б).
1. Якія факты дазваляюць зрабіць выснову, што электрастатычнае поле валодае энергіяй?
2. Якім чынам можна пераканацца ў тым, што зараджаны кандэнсатар валодае энергіяй?
3. Як можна разлічыць энергію электрастатычнага поля зараджанага кандэнсатара?
![]()
4. Растлумачце, як, выкарыстоўваючы графік залежнасці напружання паміж абкладкамі кандэнсатара ад модуля зараду на іх, можна вылічыць работу пры зарадцы кандэнсатара.
Прыклад 1. Вызначце, як і ў колькі разоў зменіцца энергія электрастатычнага поля зараджанага плоскага паветранага кандэнсатара, калі прастору паміж яго абкладкамі запоўніць газай, дыэлектрычная пранікальнасць якой ε2 = 2. Разгледзьце выпадкі: а) кандэнсатар адключаны ад крыніцы току; б) кандэнсатар падключаны да крыніцы току.
ε1 = 1
ε2 = 2
Рашэнне. Электраёмістасць паветранага кандэнсатара . Электраёмістасць гэтага кандэнсатара пасля запаўнення прасторы паміж абкладкамі газай
. Значыць,
.
У выпадку а) кандэнсатар адключаны ад крыніцы току, таму q2 = q1. Тады калі энергія электрастатычнага поля паветранага кандэнсатара , то энергія электрастатычнага поля гэтага кандэнсатара, запоўненага газай:
Такім чынам, энергія электрастатычнага поля зменшылася ў 2 разы.
У выпадку б) кандэнсатар не быў адключаны ад крыніцы току, таму напружанне паміж яго абкладкамі роўнае напружанню паміж полюсамі крыніцы току U2 = U1 = U. Тады калі энергія электрастатычнага поля паветранага кандэнсатара , то энергія электрастатычнага поля гэтага кандэнсатара, запоўненага газай:
Такім чынам, энергія электрастатычнага поля павялічылася ў 2 разы.
Адказ: а) энергія электрастатычнага поля паменшылася ў 2 разы; б) энергія электрастатычнага поля павялічылася ў 2 разы.
Прыклад 2. Плоскі паветраны кандэнсатар, плошча перакрыцця абкладак якога S = 100 см2, змясцілі ў газу з дыэлектрычнай пранікальнасцю ε = 2,0 і падключылі да крыніцы току з напружаннем на полюсах U = 120 В. Вызначце мінімальную работу, якую неабходна выканаць знешняй сіле, каб пасля адключэння кандэнсатара ад крыніцы току павольна павялічыць адлегласць паміж яго абкладкамі d1 = 1,0 см да d2 = 2,0 см.
S = 100 см2 = 1,00 · 10–2 м2
ε = 2,0
U = 120 В
d1 = 1,0 см = 1,0 · 10–2 м
d2 = 2,0 см = 2,0 · 10–2 м
Рашэнне. Модуль зараду кожнай з абкладак кандэнсатара
Энергія электрастатычнага поля кандэнсатара да змены адлегласці паміж яго аб кладкамі
Пасля адключэння кандэнсатара ад крыніцы току зарады на яго абкладках не змяняюцца.
Энергію электрастатычнага поля кандэнсатара пасля павелічэння адлегласці паміж яго пласцінамі вызначым наступным чынам:
Мінімальная работа, якую неабходна выканаць знешняй сіле, каб павялічыць адлегласць паміж абкладкамі кандэнсатара, роўная прырашчэнню энергіі электрастатычнага поля кандэнсатара, бо пры павольным павелічэнні адлегласці паміж абкладкамі кандэнсатара іх кінетычная энергія застаецца блізкай да нуля.
Адказ: .
Практыкаванне 18
1. Вызначце энергію электрастатычнага поля кандэнсатара электраёмістасцю C = 0,20 мкФ, калі напружанне на ім U = 200 В.
2. Модуль напружанасці аднароднага электрастатычнага поля паміж абкладкамі плоскага паветранага кандэнсатара . Вызначце адлегласць паміж абкладкамі, калі плошча іх перакрыцця S = 100 см2, а энергія электрастатычнага поля кандэнсатара W = 35,4 мкДж.
3. Энергія электрастатычнага поля зараджанага плоскага кандэнсатара W1 = 5 мкДж, калі паміж яго абкладкамі знаходзіцца газа, дыэлектрычная пранікальнасць якой ε1 = 2. Вызначце энергію поля гэтага кандэнсатара, калі прастора паміж яго абкладкамі будзе запоўнена трансфарматарным алеем, дыэлектрычная пранікальнасць якога ε2 = 2,5.
4. Плоскі кандэнсатар, плошча перакрыцця абкладак якога S = 40 см2, а адлегласць паміж імі d = 8,0 мм, запоўнены трансфарматарным алеем з дыэлектрычнай пранікальнасцю ε = 2,5. Вызначце энергію і модуль напружанасці электрастатычнага поля кандэнсатара, калі напружанне на ім U = 200 В.
5. Плоскі кандэнсатар падключылі да крыніцы току і зарадзілі да напружання U<sub>1 = 220 В. Адключыўшы кандэнсатар ад крыніцы току, павялічылі адлегласць паміж яго абкладкамі ад d1 = 1,0 см да d2 = 3,0 см. Вызначце модуль напружанасці электрастатычнага поля і напружанне паміж абкладкамі кандэнсатара пасля іх рассоўвання.
![]()
6. Плоскі паветраны кандэнсатар падключылі да крыніцы току. Як зменяцца электраёмістасць, напружанне і патэнцыяльная энергія ўзаемадзеяння зарадаў на абкладках кандэнсатара, калі павялічыць адлегласць паміж яго абкладкамі? Да кожнага элемента першага слупка падбярыце адпаведны элемент з другога.
|
Фізічная велічыня |
Змяненне велічыні |
|
А. Электраёмістасць Б. Напружанне В. Патэнцыяльная энергія |
1. Павялічыцца 2. Паменшыцца 3. Не зменіцца |
7. Да кандэнсатара электраёмістасцю С1 = 0,10 мкФ, напружанне паміж абкладкамі якога U = 1,6 · 102 В, паралельна падключылі першапачаткова незараджаны кандэнсатар электраёмістасцю С2 = С1 = 0,10 мкФ. Вызначце энергію батарэі пасля злучэння кандэнсатараў.