§ 19. Напружанасць электрастатычнага поля. Прынцып суперпазіцыі
| Сайт: | Профильное обучение |
| Курс: | Фізіка. 10 клас |
| Книга: | § 19. Напружанасць электрастатычнага поля. Прынцып суперпазіцыі |
| Напечатано:: | Гость |
| Дата: | Воскресенье, 6 Июль 2025, 08:52 |
Для вывучэння ўласцівасцей электрастатычнага поля зручна вы ка рыстоў ваць такую яго характарыстыку, якая не залежыць ад лікавага зна чэння пробнага зараду і дазваляе вызначыць сілу, што дзейнічае на зарад з боку поля ў любым яго пункце. Для гравітацый нага поля характарыстыкай, якая не залежыць ад масы цела, з’яўляецца паскарэнне свабоднага падзення . А якая фізічная велічыня з’яўляецца ха рак тарыстыкай электрастатычнага поля?
Напружанасць электрастатычнага поля. Няхай электрастатычнае поле створана ў вакууме пунктавым зарадам Q > 0. Калі ў пэўны пункт поля змясціць пробны дадатны зарад q0, на яго будзе дзейнічаць кулонаўская сіла адштурхвання, модуль якой .
Сіла не можа з’яўляцца характарыстыкай поля, бо яе модуль прапарцыянальны значэнню пробнага зараду q0. Аднак адносіны модуля сілы, якой электрастатычнае поле пунктавага зараду Q дзейнічае на пробны зарад q0, не залежаць ад значэння пробнага зараду:
,
(19.1)
а значыць, могуць служыць характарыстыкай поля.
Гэтая характарыстыка атрымала назву напружанасць электрастатычнага поля і яе абазначаюць . Напружанасць характарызуе сілавое дзеянне поля на ўнесеныя ў яго зарады.
Напружанасць электрастатычнага поля — фізічная вектарная велічыня, роўная адносінам сілы, якой поле дзейнічае на пробны зарад, да значэння гэтага зараду:
(19.2)
З улікам выразаў (19.1) і (19.2) можна вызначыць модуль напружанасці элек тра статычнага поля, створанага пунктавым зарадам Q, у пункце, які зна ходзіц ца на адлегласці r ад яго:
Такім чынам, модуль напружанасці поля, стваранага ў вакууме пунктавым зарадам, прама прапарцыянальны модулю гэтага зараду і адваротна прапарцыянальны квадрату адлегласці паміж зарадам і пунктам, у якім вызначаюць значэнне напружанасці.
Калі зарад Q знаходзіцца ў аднародным асяроддзі з дыэлектрычнай пранікаль насцю ε, то модуль напружанасці поля .
З выразу вынікае, што адзінкай напружанасці электрастатычнага поля ў СІ з’яўляецца ньютан на кулон
. Аднак у СІ шырока выкарыстоў ваюць іншую назву гэтай адзінкі — вольт на метр
.
Ведаючы напружанасць электрастатычнага поля, можна вызначыць сілу, якая дзейнічае на любы пунктавы зарад у любым пункце гэтага поля:
(19.3)
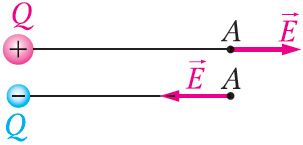
Напружанасць поля, як і сіла, велічыня вектарная. Напрамак напружанасці поля супадае з напрамкам сілы, якая дзейнічае на дадатны пробны электрычны зарад. Напружанасць у любым пункце электрастатычнага поля пунктавага зараду накіравана ўздоўж прамой, што злучае гэты пункт і пунктавы зарад, які стварае поле. Напружанасць поля, створанага пунктавым дадатным зарадам Q > 0, накіравана ад зараду, а напружанасць поля, створанага пунктавым адмоўным зарадам Q < 0, — да зараду (мал. 104).
1. Як зменіцца модуль напружанасці ў некаторым пункце поля, створанага пунктавым зарадам Q, калі: а) адлегласць r ад зараду да гэтага пункта павялічыць удвая; б) зарад Q павялічыць удвая, а адлегласць r ад зараду да гэтага пункта паменшыць удвая?
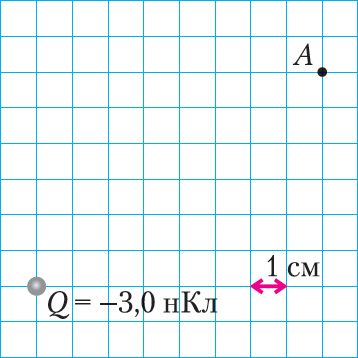
2. Як накіравана ў пункце А напружанасць поля, створанага нерухомым пунктавым зарадам (мал. 105)? Чаму роўны модуль напружанасці поля ў гэтым пункце?
![]()
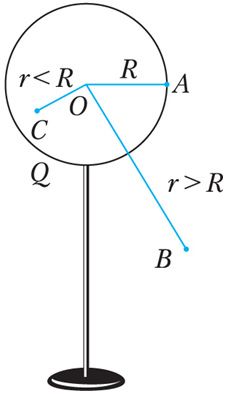
Модуль напружанасці поля адасобленай праводнай сферы радыусам R, зарад якой Q (мал. 105.1), у пунктах на яе паверхні r = R і за сферай на адлегласці r = R ад яе цэнтра вызначаюць па формуле . У пунктах, якія знаходзяцца ўнутры праводнай сферы r < R, напружанасць роўная нулю
, калі ўнутры гэтай сферы няма электрычных зарадаў.
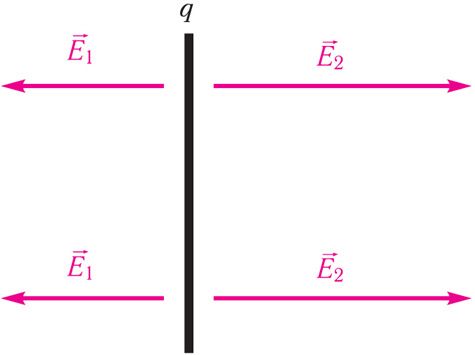
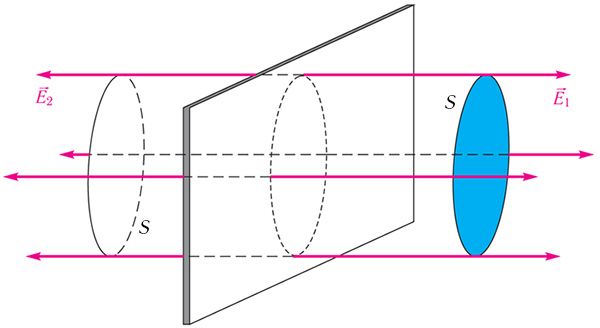
Напружанасць электрастатычнага поля, створанага раўнамерна зараджанай бясконцай плоскасцю, аднолькавая ва ўсіх пунктах паўпрасторы з кожнага боку ад плоскасці (пры гэтым ), а яе модуль
дзе S — плошча некаторага ўчастка плоскасці, — модуль зараду гэтага ўчастка (мал. 105.2).
Цікава ведаць
Акрамя гравітацыйнага поля, у Зямлі ёсць электрычнае і магнітнае палі. Модуль напружанасці электрычнага поля каля паверхні Зямлі ў сярэднім складае . Электрычнае поле Зямлі змяняецца з цягам часу. Залішні адмоўны электрычны зарад зямнога шара вагаецца каля –6 · 105 Кл.
Прынцып суперпазіцыі электрычных палёў. Няхай пробны зарад q0 знаходзіцца ў пэўным пункце электрастатычнага поля, створанага не адным, а некалькімі пунктавымі зарадамі. Эксперыментальным шляхам вызначылі, што рэзультуючая сіла, якая дзейнічае на пробны зарад, роўная вектарнай суме сіл, якія дзейнічаюць з боку электрастатычных палёў гэтых пунктавых зарадаў:
(19.4)
Выкарыстаўшы формулу (19.3), можна вызначыць сілы, якія дзейнічаюць на пробны зарад:
,
,
,
, …,
,
дзе рэзультуючая напружанасць поля сістэмы пунктавых зарадаў, а
,
,
, ...,
— напружанасці палёў у дадзеным пункце, якiя ствараюцца 1-м, 2-м, 3-м, … , n-м пунктавымі зарадамі.
Падставіўшы гэтыя выразы ў суадносіны (19.4), атрымаем, што калі ў дадзеным пункце прасторы электрастатычнае поле створана сістэмай пунктавых зарадаў, то напружанасць рэзультуючага поля ў гэтым пункце роўная вектарнай суме напружанасцей палёў, якiя ствараюцца кожным з пунктавых зарадаў сістэмы паасобна:
Гэтае палажэнне носіць назву прынцып суперпазіцыі палёў.
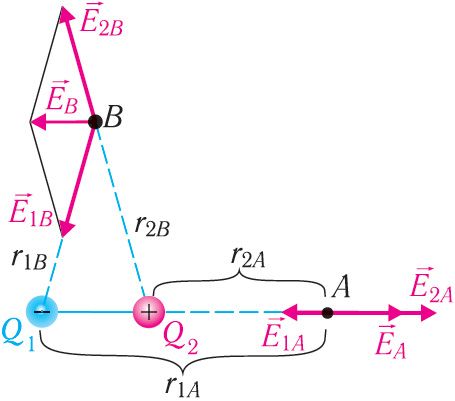
Выкарыстаем прынцып суперпазіцыі, каб вызначыць у пунктах А і В напружанасці рэзультуючага поля, створанага двума пунктавымі электрычнымі зарадамі супрацьлеглых знакаў Q1 < 0 і Q2 > 0, але з аднолькавымі модулямі (мал. 106).
Напружанасці i
палёў, створаных зарадамі Q1 і Q2, у пункце А накіраваны ўздоўж прамой, якая злучае зарады, у супрацьлеглыя бакі. Напружанасць
рэзультуючага поля ў пункце А роўная вектарнай суме напружанасцей
i
і таксама накіравана ўздоўж прамой, якая злучае зарады.
Напружанасць рэзультуючага поля ў пункце В, які знаходзіцца па-за прамой, якая злучае зарады, роўная вектарнай суме напружанасцей
i
. Вызначыць яе можна паводле правіла паралелаграма (гл. мал. 106).
![]()
Прынцып суперпазіцыі таксама выкарыстоўваецца і для вызначэння напружанасці электрастатычнага поля сістэмы праводных канцэнтрычных зараджаных сфер.
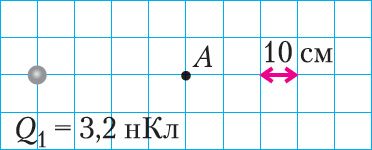
1. Чаму роўны модуль напружанасці поля, створанага пунктавым нерухомым зарадам Q1, у пункце А (мал. 107)?
2. Дзе трэба размясціць яшчэ адзін такі самы пунктавы зарад Q2 = Q1, каб у пункце А модуль напружанасці рэзультуючага поля быў роўны нулю?

![]()
1. Што называюць напружанасцю электрастатычнага поля?
2. Як разлічыць напружанасць электрастатычнага поля пунктавага зараду ў некаторым пункце гэтага поля?
3. Як вызначыць сілу, якая дзейнічае з боку электрастатычнага поля на змешчаны ў яго пунктавы зарад?
4. Ці можна назваць паскарэнне свабоднага падзення напружанасцю гравітацыйнага поля?
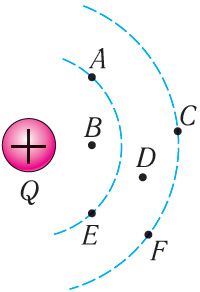
5. Пробны зарад змяшчаюць у розныя пункты электрастатычнага поля, створанага зарадам Q (мал. 108). У якіх пунктах модуль напружанасці поля максімальны? мінімальны? У якіх пунктах ён аднолькавы?
6. Як накіравана напружанасць поля, створанага пунктавым зарадам Q < 0; пунктавым зарадам Q > 0?
7. У чым заключаецца прынцып суперпазіцыі электрастатычных палёў?
![]()
8. Гравітацыйнае поле Зямлі таксама можна характарызаваць напружанасцю. Параўнайце выразы для электрычнай сілы і сілы цяжару
. Чаму роўная напружанасць гравітацыйнага поля Зямлі паблізу ад яе паверхні?
Прыклад 1. Два нерухомыя пунктавыя зарады Q1 = 6,70 нКл і Q2 = –13,3 нКл знаходзяцца ў паветры на адлегласці r = 5,00 см адзін ад аднаго. Вызначце модуль напружанасці электрастатычнага поля ў пункце, які знаходзіцца на адлегласці r1 = 3,00 см ад дадатнага зараду і r2 = 4,00 см ад адмоўнага.
Q1 = 6,70 нКл = 6,70 · 10–9 Кл
Q2 = –13,3 нКл = –1,33 · 10–8 Кл
r = 5,00 см = 5,00 · 10–2 м
r1 = 3,00 см = 3,00 · 10–2 м
r2 = 4,00 см = 4,00 · 10–2 м
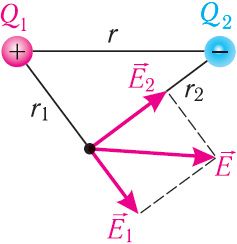
Рашэнне. Згодна з прынцыпам супер пазіцыі напружанасць рэзультуючага поля (мал. 109) вызначаюць паводле пра ві ла паралелаграма. Тут
и
— напружа насці палёў, створаных пунктавымі зарадамі Q1 и Q2 у дадзеным пункце. З умовы задачы і тэарэмы Піфагора вынікае, што вугал паміж
и
прамы.
Модуль напружанасці Е рэзультуючага поля знойдзем па тэарэме Піфагора . Паколькі зарады Q1 і Q2 пунктавыя, то
,
.
З улікам гэтага
Адказ: .
![]()
Прыклад 2. Першапачаткова нерухомы шарык маса m = 10 г і зарадам q = 1,0 мкКл пачынае падаць з паскарэннем, модуль якога а = 8,0 . Шарык знаходзіцца ў электрастатычным полі, напружанасць якога накіравана вертыкальна ўверх і аднолькавая ва ўсіх яго пунктах. Вызначце напружанасць гэтага поля.
m = 10 г = 1,0 · 10–2 кг
q = 1,0 мкКл = 1,0 · 10–6 Кл
а = 8,0

Рашэнне. У пачатковы момант на шарык дзейнічаюць сіла цяжару з боку гравітацыйнага поля Зямлі і электрычная сіла
з боку электрастатычнага поля. Модуль паскарэння, з якім пачынае падаць дадатна зараджаны шарык, меншы за модуль паскарэння свабоднага падзення
. Значыць, электрычная сіла
электрастатычнага поля накіравана вертыкальна ўверх і супадае па напрамку з напружанасцю. Модуль напружанасці вызначым, выкарыстоўваючы другі закон Ньютана:
. У праекцыі на вертыкальную вось Оу (мал. 109.1) гэтае ўраўненне мае выгляд:
. Тады
.
Адказ: напружанасць электрастатычнага поля накіравана вертыкальна ўверх і яе модуль .
Практыкаванне 14
1. У некаторы пункт электрастатычнага поля, у якім модуль напружанасці , змяшчаюць пунктавы зарад q = 4,00 нКл. Вызначце модуль сілы, якая дзейнічае на гэты зарад з боку электрастатычнага поля.
2. Вызначце модуль пунктавага зараду, які знаходзіцца ў паветры, калі на адлегласці r = 1,0 см ад зараду модуль напружанасці поля
3. Два дадатныя пунктавыя зарады знаходзяцца на адлегласці r0 = 10 см адзін ад аднаго. У пункце, размешчаным на прамой, якая злучае зарады, на адлегласці r1 = 8,0 см ад першага зараду модуль напружанасці рэзультуючага электрастатычнага поля роўны нулю. Вызначце адносіны зарадаў .
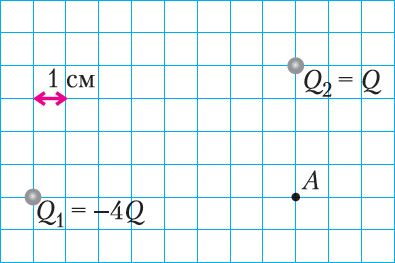
4. Электрастатычнае поле ў пэўным пункце створана нерухомымі пунктавымі зарадамі Q1 = –4Q і Q2 = Q (мал. 110).
а) Адлюструйце ў выбраным вамі маштабе напружанасці i
палёў, створаных кожным зарадам у пункце А.
б) Пазначце на малюнку напрамак рэзультуючай напружанасці .
в) Вызначце модуль рэзультуючай на пружа насці ЕА поля, калі |Q| = 8,0 нКл.
5. Пылінка масай m = 2,5 · 10–8 г мае зарад q = 5,0 · 10–12 Кл. Напружанасць поля ў пункце, дзе знаходзіцца пылінка, накіравана вертыкальна ўверх. Вызначце модуль напружанасці электрастатычнага поля, калі пылінка знаходзіцца ў раўнавазе.
![]()
6. Тры аднолькавыя адмоўныя пунктавыя зарады, модулі якіх , размешчаны ў вяршынях раўнабедранага прамавугольнага трохвугольніка. Вызначце напружанасць электрастатычнага поля ў пункце прасторы, што знаходзіцца на сярэдзіне гіпатэнузы, даўжыня якой а = 8,0 см.
7. Часціца масай m = 2,0 мг і зарадам q = 9,5 пКл пачынае рухацца ў вакууме ў электрастатычным полі, модуль напружанасці якога . Напружанасць поля аднолькавая ва ўсіх яго пунктах і накіравана гары зантальна. Вызначце модуль паскарэння гэтай часціцы і шлях, пройдзены ёю за першую секунду руху.
8. Зарад адасобленай металічнай сферы, якая знаходзіцца ў паветры, Q = 0,20 мкКл. Вызначце максімальнае значэнне напружанасці электрастатычнага поля, створанага зарадам гэтай сферы, калі яе дыяметр d = 0,80 м.
9. Бясконцую раўнамерна зараджаную плоскую пласціну змясцілі ў аднароднае электрычнае поле, напружанасць якога перпендыкулярная яе паверхні. Модулі рэзультуючых напружанасцей палёў злева і справа ад пласціны i
адпаведна (мал. 110.1). Вызначце модуль сілы, якая дзейнічае на адзінку плошчы S = 1,0 м2 пласціны.