§ 12. Работа ў тэрмадынаміцы

Сайт:	Профильное обучение
Курс:	Фізіка. 10 клас
Книга:	§ 12. Работа ў тэрмадынаміцы
Напечатано::	Гость
Дата:	Пятница, 3 Май 2024, 20:37

У 9-м класе вы даведаліся, што перадача энергіі шляхам выканання работы адбываецца ў працэсе сілавога ўзаемадзеяння цел. Гэта значыць работа, выкананая над разгляданым целам, ёсць не што іншае, як работа сіл, прыкладзеных да гэтага цела з боку ўсіх астатніх (знешніх) цел, з якімі яно ўзаемадзейнічае. Работа, выкананая над целам, можа непасрэдна змяніць любы від энергіі гэтага цела, напрыклад унутраную энергію, таму работу сілы разглядаюць як меру змены энергіі фізічнай сістэмы.

Работа ў тэрмадынаміцы. Адным са спосабаў змянення ўнутранай энергіі тэрмадынамічнай сістэмы з’яўляецца выкананне работы. Гэты спосаб характарызуецца перадачай энергіі ў працэсе механічнага ўзаемадзеяння цел. Пры гэтым механічная энергія аднаго цела пераходзіць ва ўнутраную энергію другога цела ці, наадварот, змяншэнне ўнутранай энергіі аднаго цела вядзе да павелічэння механічнай энергіі другога цела.

Такім чынам, падчас выканання работы адбываецца ператварэнне энергіі з адной формы ў другую.

Паколькі для апісання тэрмадынамічных сістэм выкарыстоўваюць макрапараметры (ціск, аб’ём, тэмпература), то работу ў тэрмадынаміцы неабходна выражаць праз гэтыя параметры.

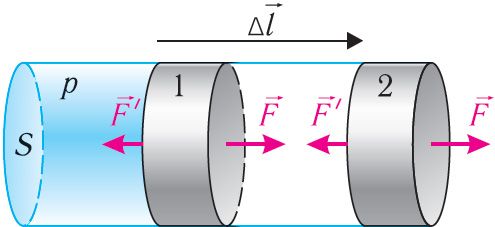
Разгледзім газ у цыліндры, закрытым поршнем, плошча якога S (мал. 66). Ціск газу ў цыліндры р. У выніку ізабарнага расшырэння газу поршань перамясціўся са становішча 1 у становішча 2 на адлегласць Δl. Модуль сілы ціску газу на поршань F = pS. Гэтая сіла выканала работу па перамяшчэнні поршня, роўную

$A subscript 12 space equals space F capital delta l cos straight alpha$ ,

дзе α — вугал паміж напрамкамі сілы $F with rightwards arrow on top$ і перамяшчэння поршня $increment l with rightwards arrow on top$ .

У дадзеным прыкладзе α = 0 і cosα = 1, то

$A subscript 12 space equals space p S capital delta l$ .

Здабытак SΔl вызначае змяненне аб’ёму ∆V = V₂ – V₁, дзе V₁ — пачатковы аб’ём газу; V₂ — аб’ём газу ў канчатковым стане (гл. мал. 66).

Такім чынам, работа сілы ціску газу пры яго ізабарным расшырэнні:

$A subscript 12 space equals space p capital delta V space equals space p left parenthesis V subscript 2 – V subscript 1 right parenthesis$ .

(12.1)

Ціск р газу — велічыня дадатная, таму з формулы (12.1) вынікае, што A₁₂ > 0.

Пры ізабарным расшырэнні газу са стану 1 у стан 2 работа сілы $F with rightwards arrow on top apostrophe$ (гл. мал. 66):

$A apostrophe subscript 12 equals space F apostrophe capital delta l cos straight beta$ ,

дзе $F apostrophe$ — модуль сілы, якая дзейнічае на газ з боку поршня (знешняя сіла); $straight beta$ — вугал паміж напрамкамі сілы $stack F apostrophe with rightwards arrow on top$ і перамяшчэння $increment l with rightwards arrow on top$ поршня.

Перамяшчэнне $increment l with rightwards arrow on top$ поршня адно і тое ж, а сіла ціску $F with rightwards arrow on top$ ггазу на поршань і сіла ціску $stack F apostrophe with rightwards arrow on top$ поршня на газ — сілы, якія падпарадкоўваюцца трэцяму закону Ньютана:

$F with rightwards arrow on top space equals space minus stack F apostrophe with rightwards arrow on top$ .

Значыць, работа $A subscript 12 apostrophe$ і работа $A subscript 12$ адрозніваюцца толькі знакам ( $cos straight beta space equals space cos 180 degree space equals space minus 1$ ):

$A subscript 12 apostrophe space equals space minus A subscript 12 space equals space minus p increment V$ .

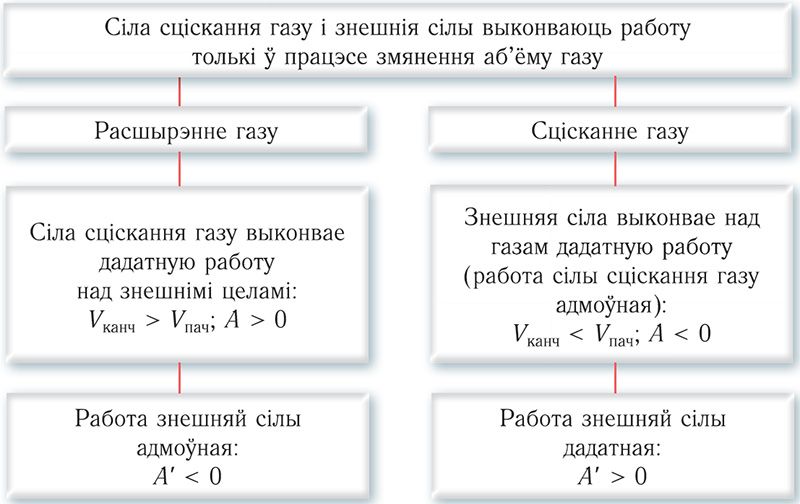
Такім чынам, можна зрабіць наступныя высновы.

Ад тэорыі да практыкі

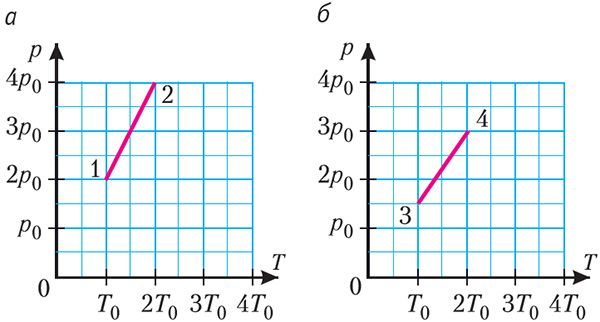
На малюнку 67, а паказаны працэс пераходу ідэальнага газу пэўнай масы са стану 1 у стан 2, а на малюнку 67, б — працэс пераходу гэтага ж газу са стану 3 у стан 4. Параўнайце работы, выкананыя сілай ціску газу ў абодвух працэсах, і змены значэнняў яго ўнутранай энергіі.

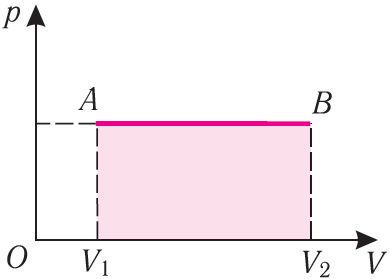
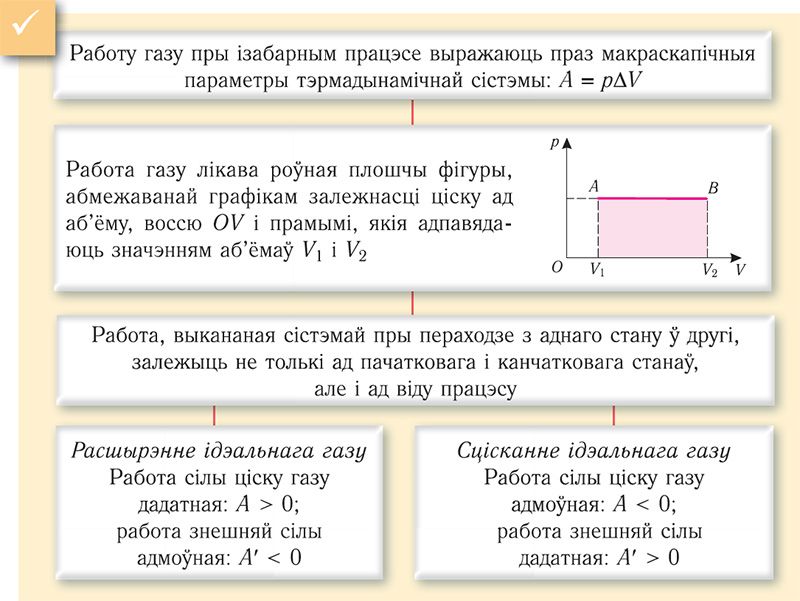
Геаметрычнае тлумачэнне работы. Работу газу можна вызначыць з дапамогай графіка. Пабудуем графік залежнасці ціску газу ад яго аб’ёму пры р = const (мал. 68). Калі працэс пераходу газу з пачатковага стану ў канчатковы з’яўляецца ізабарным (АВ — ізабара), то работа сілы ціску газу лікава роўная плошчы прамавугольніка V₁АВV₂.

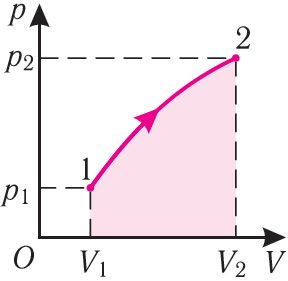
Калі працэс пераходу газу з пачатковага стану ў канчатковы не з’яўляецца ізабарным (мал. 69), то работа сілы ціску газу пры змене аб’ёму ад V₁ да V₂ лікава роўная плошчы фігуры, абмежаванай графікам працэсу (крывая 1 → 2), воссю ОV і прамымі, якія адпавядаюць значэнням аб’ёмаў V₁ і V₂.

Адсылка да электроннага дадатку для павышанага ўзроўню

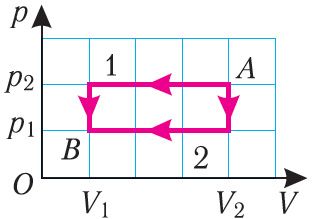
Працэс, пры якім тэрмадынамічная сістэма, прайшоўшы некаторую паслядоўнасць станаў, вяртаецца ў зыходны стан, называюць цыклічным працэсам або цыклам (мал. 69.1). Работа, выкананая сістэмай пры цыклічным працэсе, або работа цыкла, лікава роўная плошчы фігуры, абмежаванай лініямі, якія адлюстроўваюць цыкл у каардынатах р, V:

A = A₁₂ + A₂₃ + A₃₁ = S₁₂ + S₂₃ + S₃₁ = S₁₂ + S₃₁ = S₁₂₃₁,

дзе S₂₃ = 0, S₁₂₃₁ > 0 на малюнку 69.1, а і S₁₂₃₁ < 0 на малюнку 69.1, б.

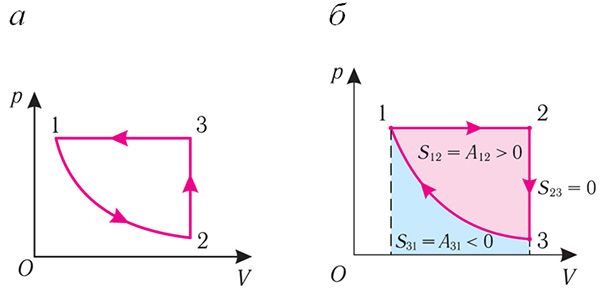
Калі «крывая расшырэння» (ізабара 1 → 2) (мал. 69.1, а) размешчана вышэй «крывой сціскання» (ізатэрма 3 → 1), то поўная работа, выкананая сістэмай за цыкл (работа цыкла), дадатная. Калі ж, як паказана на малюнку 69.1, б, «крывая сціскання» (ізабара 3 → 1) размешчана вышэй «крывой расшырэння» (ізатэрма 1 → 2), то работа цыкла адмоўная.

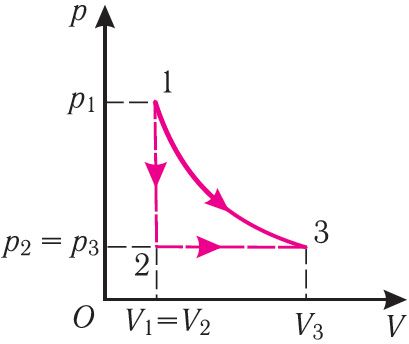
Работу газу вызначаюць не толькі пачатковы і канчатковы станы сістэмы, але і від працэсу. Напрыклад, газ са стану 1 можна перавесці ў стан 3 або ў выніку ізатэрмічнага расшырэння (мал. 70), або спачатку ізахорна панізіўшы яго ціск да значэння р₂, а затым ізабарна павялічыўшы яго аб’ём да значэння V₃. У першым выпадку работа газу большая, чым у другім.

Такім чынам, работа, выкананая тэрмадынамічнай сістэмай пры пераходзе з аднаго стану ў другі, залежыць не толькі ад пачатковага і канчатковага станаў сістэмы, але і ад віду працэсу.

Ад тэорыі да практыкі

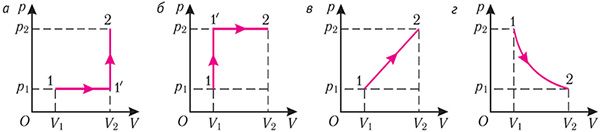
На якім з графікаў, прыведзеных на малюнках 71, а–г, сіла ціску газу выконвае ў працэсе пераходу са стану 1 у стан 2:

а) найбольшую работу; б) найменшую работу?

1. Як можна вылічыць работу, якую выконвае сіла ціску газу пры яго расшырэнні (сцісканні)?

2. Як суадносяцца паміж сабой работа сілы ціску газу і работа знешніх сіл над газам?

3. У чым заключаецца геаметрычны сэнс паняцця «работа» ў тэрмадынаміцы?

4. Чаму расшырэнне газу пры адсутнасці цеплаабмену з навакольным асяроддзем суправаджаецца яго ахаладжэннем?

5. Iдэальны газ пераводзяць са стану А ў стан В двума спосабамі: першы раз — А1В, а другі — А2В (мал. 72). У якім выпадку работа, якую выконвае сіла ціску газу, большая? У якім выпадку змена ўнутранай энергіі большая?

Прыклады рашэння задач

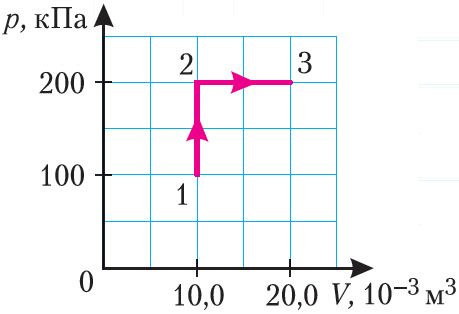
Прыклад 1. Вызначце работу, якую выконвае сіла ціску ідэальнага газу пэўнай масы пры яго пераходзе са стану 1 у стан 3 (мал. 73).

Рашэнне. I спосаб. Работа А газу падчас усяго працэсу роўная суме работ на ўчастках 1 → 2 і 2 → 3. Паколькі пры пераходзе газу са стану 1 у стан 2 яго аб’ём не змяняецца (ізахорны працэс V₂ = V₁), то работа, якую выконвае сіла ціску газу, А₁₂ = 0. У працэсе ізабарнага расшырэння (пераход газу са стану 2 у стан 3) сіла ціску газу выконвае работу

A₂₃ = p₂ΔV = p₂(V₃ – V₁).

Тады пры пераходзе са стану 1 у стан 3 работа

А = А₁₂ + А₂₃ = p₂(V₃– V₁).

А = 2,00 · 10⁵ Па · (2,00 · 10^–2 м³ – 1,00 · 10^–2 м³) = 2,00 · 10³ Дж = 2,00 кДж.

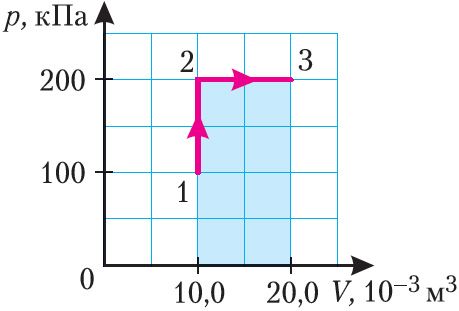
II спосаб. Работа газу лікава роўная плошчы зафарбаванай фігуры, абмежаванай графікам залежнасці ціску ад аб’ёму, воссю ОV і прамымі, якія адпавядаюць значэнням аб’ёмаў V₁ = 10,0 · 10^–3 м³ і V₂ = 20,0 · 10^–3 м³ (зафар- баваная частка на малюнку 74).

А = 2,00 · 10⁵ Па · (2,00 · 10^–2 м³ – 1,00 · 10^–2 м³) = 2,00 · 10³ Дж = 2,00 кДж.

Адказ: А = 2,00 кДж.

Прыклад 2. Вызначце работу, якую выконвае сіла ціску ідэальнага газу пэўнай масы пры ізабарным павышэнні яго тэмпературы ад t₁ = 12 °С да t₂ = 87 °С, калі ціск газу p = 190 кПа, а яго пачатковы аб’ём V₁ = 6,0 дм³.

Дадзена:
Т₁ = 285 К
Т₂ = 360 К
p = 190 кПа = 1,90 · 10⁵ Па
V₁ = 6,0 дм³ = 6,0 · 10^–3 м³

А — ?

Рашэнне. Сіла ціску газу выконвае дадатную работу, бо пры ізабарным награванні павялічваецца яго аб’ём. Таму

$A space equals space p left parenthesis V subscript 2 space – space V subscript 1 right parenthesis space equals space p V subscript 2 space – space p V subscript 1$ .

Згодна з ураўненнем Клапейрона — Мендзялеева, $p V subscript 1 space equals space nu R T subscript 1$ і $p V subscript 2 space equals space nu R T subscript 2$ . Значыць,

$A space equals space v R left parenthesis T subscript 2 space minus space T subscript 1 right parenthesis space equals space v R T subscript 1 open parentheses T subscript 2 over T subscript 1 minus 1 close parentheses space equals space p V subscript 1 open parentheses T subscript 2 over T subscript 1 minus 1 close parentheses$ .

$A space equals space 1 comma 90 times 10 to the power of 5 space Па space times 6 comma 0 times 10 to the power of negative 3 end exponent space space straight м cubed times open parentheses fraction numerator 360 space straight К over denominator 285 space straight К end fraction minus 1 close parentheses space equals space 3 comma 0 times 10 squared space Дж space equals space 0 comma 30 space кДж$ .

Адказ: $A space equals space 0 comma 30 space кДж$ .

Адсылка да электроннага дадатку для павышанага ўзроўню

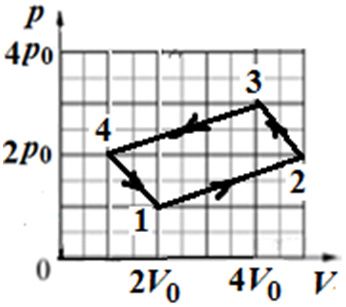
Прыклад 3. На малюнку 74.1 адлюстраваны працэс змянення стану ідэальнага газу пэўнай масы. На якім участку сіла ціску газу выканала найменшую дадатную работу? На якім участку знешняя сіла выканала найбольшую дадатную работу?

Рашэнне. Рабоце сілы ціску газу адпавядае плошча пад графікам працэсу. Пры расшырэнні газу сіла ціску выконвае дадатную работу, а знешняя сіла — адмоўную. Пры сцісканні газу наадварот: сіла ціску выконвае адмоўную работу, а знешняя сіла — дадатную. Аналіз графіка дазваляе зрабіць выснову, што ў працэсе пераходу са стану 4 у стан 1 сіла ціску газу выканала мінімальную дадатную работу (газ расшыраўся, але плошча пад графікам мінімальная). Максімальную ж дадатную работу знешняя сіла выконвае пры сцісканні, калі плошча пад графікам максімальная (гэта працэс пераходу са стану 3 у стан 4).

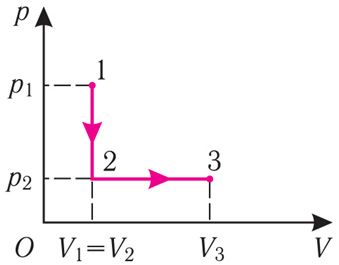
Прыклад 4. Стан ідэальнага газу, узятага ў колькасці ν = 1,0 моль пры абсалютнай тэмпературы Т₁ = 300 К, змяняецца так, як паказана на малюнку 74.2. Вызначце работу газу на працягу ўсяго працэсу, калі на ізахоры 1 → 2 яго ціск памяншаецца ў тры разы, а пункты 1 і 3 ляжаць на адной ізатэрме.

Дадзена:
ν = 1,0 моль
Т₁ = 300 К
p₁ = 3p₂
Т₁ = Т₃

A — ?

Рашэнне. Работа А газу на працягу ўсяго працэсу роўная суме значэнняў работы на участках 1 → 2 i 2 → 3 (мал. 74.2). Паколькі пры пераходзе са стану 1 у стан 2 аб'ём газу не мяняецца (працэс ізахорны V₂ = V₁), то работа газу А₁₂ = 0. Ціск газу пры пераходзе са стану 2 у стан 3 застаецца пастаянным (р₂ = р₃), значыць, работа газу А₂₃ = p₂(V₃ − V₁). Тады А = А₁₂ + А₂₃ = p₂(V₃ − V₁). Паводле ўмовы Т₁ = Т₃, таму выкарыстаем ураўненне Клапейрона: $fraction numerator p subscript 1 V subscript 1 over denominator T subscript 1 end fraction equals fraction numerator p subscript 2 V subscript 3 over denominator T subscript 3 end fraction$ , адкуль $V subscript 3 equals p subscript 1 over p subscript 2 V subscript 1 equals 3 V subscript 1$ . Такім чынам, $A equals p subscript 2 open parentheses 3 V subscript 1 minus V subscript 1 close parentheses equals 2 p subscript 2 V subscript 1 equals fraction numerator 2 p subscript 1 V subscript 1 over denominator 3 end fraction$ .

Згодна з ураўненнем Клапейрона — Мендзялеева, p₁V₁ = νRT₁. Тады $A equals 2 over 3 nu R T subscript 1$ .

$A equals fraction numerator 2 times 1 comma 0 space моль times 8 comma 31 space begin display style fraction numerator Дж over denominator straight К times моль end fraction end style times 300 space straight К over denominator 3 end fraction equals 1662 space Дж equals 1 comma 7 space кДж.$

Адказ: А = 1,7 кДж.

Практыкаванне 8

1. Сіла ціску ідэальнага аднаатамнага газу пэўнай масы выконвае адмоўную работу падчас ізатэрмічнага працэсу. Як змяняюцца ў гэтым працэсе аб’ём, ціск і ўнутраная энергія газу?

2. Газ, ціск якога p = 0,10 МПа, ізабарна расшыраецца. Пры гэтым сіла ціску газу выконвае работу А = 40 Дж. Вызначце, на колькі павялічыўся аб’ём газу.

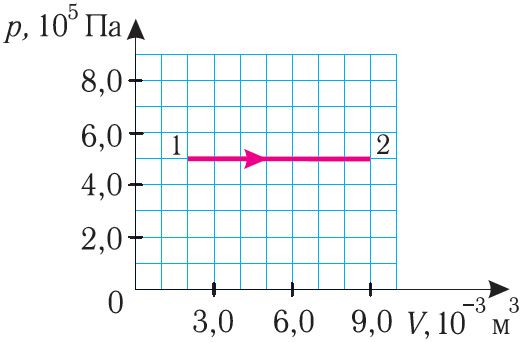
3. На малюнку 75 прыведзены графік залежнасці ціску газу ад аб’ёму. Вызначце работу, якую выканае сіла ціску газу пры расшырэнні.

4. Пры ізабарным павелічэнні тэмпературы азоту на ΔT = 180 К сілай яго ціску выканана работа А = 25 кДж. Вызначце масу азоту.

5. Ідэальны газ пэўнай масы, тэмпература якога T₁ = 290 К і ціск p = 0,20 МПа, займае аб’ём V₁ = 0,10 м³. Вызначце работу, якую выканае сіла ціску газу пры яго ізабарным награванні да тэмпературы T₂ = 370 К.

Адсылка да электроннага дадатку для павышанага ўзроўню

6. Пры расшырэнні ідэальнага газу, колькасць рэчыва якога ν = 3 моль, яго аб’ём павялічыўся ад V₁ = 2 дм³ да V₂ = 6 дм³. Абсалютная тэмпература газу змянялася па законе T = αV², дзе $straight alpha equals 1 times 10 to the power of 7 space straight К over straight м to the power of 6$ — каэфіцыент прапарцыянальнасці. Вызначце работу, выкананую сілай ціску газу пры яго расшырэнні.

§ 12. Работа ў тэрмадынаміцы

Оглавление