§ 3. Макра- і мікрапараметры. Ідэальны газ. Асноўнае ўраўненне малекулярна-кінетычнай тэорыі ідэальнага газу

Сайт:	Профильное обучение
Курс:	Фізіка. 10 клас
Книга:	§ 3. Макра- і мікрапараметры. Ідэальны газ. Асноўнае ўраўненне малекулярна-кінетычнай тэорыі ідэальнага газу

Напечатано::	Гость
Дата:	Saturday, 5 September 2026, 07:54

Найбольш простым з усіх агрэгатных станаў рэчыва з’яўляецца газападобны. Таму вывучэнне ўласцівасцей рэчываў пачынаюць з газаў. Газ (грэч. сhaos — хаос) — такі агрэгатны стан рэчыва, калі часціцы, што яго складаюць, амаль свабодна і хаатычна рухаюцца паміж сутыкненнямі, падчас якіх адбываецца рэзкае змяненне іх скорасці. Тэрмін «газ» прапанаваў на пачатку XVII ст. нідэрландскі хімік Ян Батыст ван Гельмант (1579–1644).

Макра- і мікрапараметры. Пры вывучэнні механікі ў 9-м класе вы пазнаёміліся з паняццем «стан механічнай сістэмы цел». Параметрамі гэтага стану з’яўляюцца каардынаты, скорасці або імпульсы цел. У цеплавых працэсах асноўнымі фізічнымі велічынямі, якія характарызуюць стан макраскапічных цел без уліку іх малекулярнай будовы, з’яўляюцца ціск p, аб’ём V і тэмпература T. Гэтыя фізічныя велічыні называюць макраскапічнымі параметрамі стану. Да мікраскапічных параметраў стану цел адносяць індывідуальныя характарыстыкі малекул: масу асобнай малекулы m₀, скорасць $nu with rightwards arrow on top$ , імпульс $rho with rightwards arrow on top$ і кінетычную энергію Е_к яе цеплавога руху.

Адна з галоўных задач малекулярна-кінетычнай тэорыі заключаецца ў вызначэнні сувязі паміж макраскапічнымі і мікраскапічнымі параметрамі.

Ідэальны газ. Для тэарэтычнага тлумачэння ўласцівасцей газаў выкарыстоўваюць іх спрошчаную мадэль — ідэальны газ.

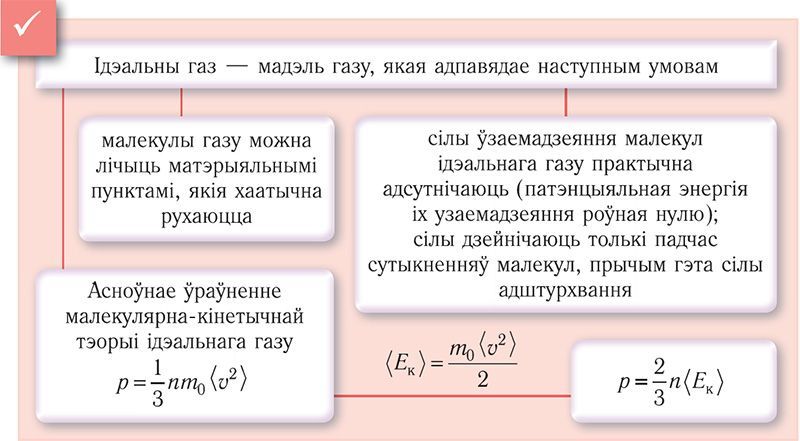
Ідэальны газ — мадэль газу, якая адпавядае наступным умовам: 1) малекулы газу можна лічыць матэрыяльнымі пунктамі, якія хаатычна рухаюцца; 2) сілы ўзаемадзеяння паміж малекуламі ідэальнага газу практычна адсутнічаюць (патэнцыяльная энергія іх узаемадзеяння роўная нулю); сілы дзейнічаюць толькі падчас сутыкненняў малекул, прычым гэта сілы адштурхвання.

Паводзіны малекул ідэальнага газу можна апісаць, выкарыстаўшы законы Ньютана і ўлічыўшы, што паміж сутыкненнямі малекулы рухаюцца практычна раўнамерна і прамалінейна.

Мадэль ідэальнага газу можна прымяняць у абмежаваным дыяпазоне тэмператур і пры дастаткова малым ціску. Так, напрыклад, уласцівасці вадароду і гелію пры нармальным атмасферным ціску і пакаёвай тэмпературы блізкія да ўласцівасцей ідэальнага газу.

Вывучаючы фізіку ў 7-м класе, вы даведаліся, што ціск газу на сценкі пасудзіны, у якой ён знаходзіцца, як і на любое цела, змешчанае ўнутр пасудзіны, абумоўлены ўдарамі часціц, якія ўтвараюць газ (мал. 14).

Адсылка да электроннага дадатку для павышанага ўзроўню

Вывядзенне асноўнага ўраўнення малекулярна-кінетычнай тэорыі ідэальнага газу. З пункта гледжання малекулярна-кінетычнай тэорыі ціск газу ўзнікае ў выніку ўдараў малекул, што ўтвараюць газ, па целе, з якім датыкаюцца (мал. 14). Пры ўдары імпульс малекулы газу змяняецца: $increment p with rightwards arrow on top equals m subscript 0 v with rightwards arrow on top minus m subscript 0 nu with rightwards arrow on top subscript 0$ , дзе m₀ — яе маса, а $nu with rightwards arrow on top subscript 0$ і $nu with rightwards arrow on top$ — скорасці перад ударам і пасля яго. Калі Δt — прамежак часу паміж двума паслядоўнымі ўдарамі аб цела адной і той малекулы, то сярэдняй сіле $open angle brackets F with rightwards arrow on top subscript straight м close angle brackets$ , якой цела дзейнічае на малекулу падчас удару працягласцю δt, адпавядае сярэдняя сіла $open angle brackets F with rightwards arrow on top subscript 1 сц end subscript close angle brackets$ , якой адна малекула дзейнічае на цела (напрыклад, на сценку пасудзіны) на працягу прамежку часу Δt. Выкарыстаўшы другі закон Ньютана для апісання ўдару малекулы $open angle brackets F with rightwards arrow on top subscript straight м close angle brackets straight delta t equals m subscript 0 v with rightwards arrow on top minus m subscript 0 v with rightwards arrow on top subscript 0$ і трэці закон Ньютана для імгненных значэнняў сіл узаемадзеяння малекулы і цела $F with rightwards arrow on top subscript straight м equals negative F with rightwards arrow on top subscript 1 сц end subscript$ , атрымаем для ўведзеных вышэй сярэдняй сілы $open angle brackets F with rightwards arrow on top subscript straight м close angle brackets$ і сярэдняй сілы з прамежкам часу дзеяння Δt:

$open angle brackets F with rightwards arrow on top subscript straight м close angle brackets delta t equals m subscript 0 v with rightwards arrow on top minus m subscript 0 v with rightwards arrow on top subscript 0 equals negative open angle brackets F with rightwards arrow on top subscript 1 сц end subscript close angle brackets increment t.$

(3.0)

Пры нармальных умовах і макраскапічных памерах пасудзіны колькасць удараў малекул газу аб плоскую паверхню плошчай 1 см² складае каля 10²⁴ у секунду. Вельмі слабыя сілы ўдараў асобных малекул $open angle brackets F with rightwards arrow on top subscript 1 сц end subscript close angle brackets$ складваюцца для вялізнай колькасці малекул у значную па велічыні і амаль пастаянную сілу, якая дзейнічае на цела. Усярэдненае па часе значэнне гэтай сілы, аднесенае да адзінкавай пляцоўкі, і ёсць ціск газу.

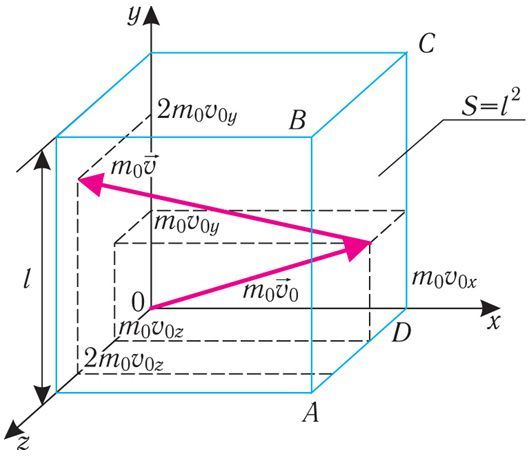
Няхай у пасудзіне, якая мае форму куба з рабром даўжынёй l (мал. 14.1), знаходзіцца ідэальны газ, які складаецца з аднолькавых малекул масай m₀ кожная. Будзем лічыць, што малекулы пругка ўдараюцца толькі аб сценкі пасудзіны, не сутыкаючыся адна з адной. Паколькі малекулы, якія ўтвараюць сценкі пасудзіны, выконваюць цеплавыя ваганні, то скорасці руху малекул газу пры сутыкненнях з імі змяняюцца выпадковым чынам. Аднак калі газ і пасудзіна знаходзяцца ў цеплавой раўнавазе, то сярэдняя кінетычная энергія малекул не змяняецца з часам. Гэта дазваляе рэальны хаатычны рух малекул газу з разнастайнымі напрамкамі і модулямі скарасцей спрошчана разглядаць як рух, пры якім модулі праекцый скорасці на кожную з каардынатных восей аднолькавыя, гэта значыць $open vertical bar v subscript x close vertical bar equals open vertical bar v subscript y close vertical bar equals open vertical bar v subscript z close vertical bar$ , і застаюцца нязменнымі, а пры суткненнях змяняецца знак толькі ў адной з трох праекцый скорасці на каардынатныя восі.

Для апісання ўдару малекулы газу аб сценку ABCD (мал. 14.1) запішам суадносіны (3.0) у праекцыях на каардынатныя восі:

$open angle brackets F subscript straight м space x end subscript close angle brackets delta t equals increment p subscript x equals m subscript 0 v subscript x minus m subscript 0 v subscript 0 x end subscript equals m subscript 0 v subscript x minus left parenthesis negative m subscript 0 v subscript x right parenthesis equals 2 m subscript 0 v subscript x equals negative 2 m subscript 0 v subscript 0 x end subscript equals negative open angle brackets F subscript 1 сц space x end subscript close angle brackets increment t semicolon$

$open angle brackets F subscript straight м space y end subscript close angle brackets delta t equals increment p subscript y equals m subscript 0 v subscript y minus m subscript 0 v subscript 0 y end subscript equals 0 semicolon$ $open angle brackets F subscript straight м space z end subscript close angle brackets delta t equals increment p subscript z equals m subscript 0 v subscript z minus m subscript 0 v subscript 0 z end subscript equals 0.$

Паколькі прамежак часу паміж двума паслядоўнымі сутыкненнямі малекулы са сценкай ABCD $increment t equals fraction numerator 2 l over denominator v subscript 0 x end subscript end fraction$ , то

$open angle brackets F subscript 1 сц space x end subscript close angle brackets equals negative fraction numerator increment p subscript x over denominator increment t end fraction equals fraction numerator 2 m subscript 0 v subscript 0 x end subscript over denominator increment t end fraction equals fraction numerator 2 m subscript 0 v subscript 0 x end subscript superscript 2 over denominator 2 l end fraction equals fraction numerator m subscript 0 v subscript 0 x end subscript superscript 2 over denominator l end fraction.$

Праекцыя поўнай сярэдняй сілы, якой усе N малекул, што знаходзяцца ў посудзіне, дзейнічаюць на сценку ABCD, $open angle brackets F subscript сц close angle brackets equals open angle brackets F subscript 1 сц space x end subscript close angle brackets times N$ , бо $open angle brackets F subscript 1 сц space y end subscript close angle brackets equals 0$ і $open angle brackets F subscript 1 сц space z end subscript close angle brackets equals 0$ .

Значыць, $open angle brackets F subscript сц close angle brackets equals N fraction numerator m subscript 0 open angle brackets v subscript x superscript 2 close angle brackets over denominator l end fraction$ дзе $open angle brackets v subscript x superscript 2 close angle brackets$ — усярэднены па ўсіх N часціцах квадрат праекцый іх скарасцей на вось Ох.

Раздзяліўшы абедзве часткі суадносін для $open angle brackets F subscript сц close angle brackets$ на плошчу сценкі S = l₂, атрымаем формулу для ціску, які малекулы газу робяць на сценку ABCD:

$p equals fraction numerator N m subscript 0 open angle brackets v subscript x superscript 2 close angle brackets over denominator l cubed end fraction.$

Паколькі $v squared equals v subscript x superscript 2 plus v subscript y superscript 2 plus v subscript z superscript 2$ , то $open angle brackets v squared close angle brackets equals open angle brackets v subscript x superscript 2 close angle brackets plus open angle brackets v subscript y superscript 2 close angle brackets plus open angle brackets v subscript z superscript 2 close angle brackets$ . Малекулы газу ў сярэднім зусім аднолькава адбіваюцца ад трох пар супрацьлегла размешчаных граней куба, таму $open angle brackets v subscript x superscript 2 close angle brackets equals open angle brackets v subscript y superscript 2 close angle brackets equals open angle brackets v subscript z superscript 2 close angle brackets equals 1 third open angle brackets v squared close angle brackets$ . З улікам таго, што газ займае объём V = l₃, а канцэнтрацыя малекул газу $n equals N over V$ , атрымаем:

$p equals 1 third n m subscript 0 open angle brackets v squared close angle brackets.$

(3.1)

Выраз (3.1) называюць асноўным ураўненнем малекулярнакінетычнай тэорыі ідэальнага газу. Гэтае ўраўненне дазваляе разлічыць макраскапічны параметр ціск p ідэальнага газу праз масу m₀ малекулы, канцэнтрацыю n малекул і сярэднюю квадратычную скорасць іх цеплавога руху, вызначаную па формуле $open angle brackets v subscript кв close angle brackets space equals space square root of open angle brackets v squared close angle brackets end root$ . Формула (3.1) звязвае паміж сабой макра- і мікраскапічныя параметры сістэмы «ідэальны газ».

З асноўнага ўраўнення малекулярна-кінетычнай тэорыі ідэальнага газу вынікае, што ціск з'яўляецца сярэдняй велічынёй, і, значыць, гэтае паняцце нельга прымяняць да асобнай малекулы.

Адсылка да электроннага дадатку для павышанага ўзроўню

Залежнасць ціску газу ад сярэдняга значэння квадрата скорасці $open angle brackets v squared close angle brackets$ цеплавога руху яго малекул абумоўлена тым, што з павелічэннем скорасці, папершае, узрастае імпульс малекулы, а значыць, і сіла ўдару аб сценку. Падругое, узрастае колькасць удараў, бо малекулы часцей сутыкаюцца са сценкамі.

Ад тэорыі да практыкі

У герметычна закрытай пасудзіне знаходзіцца ідэальны газ. Калі частку газу праз клапан выпусціць з пасудзіны, то як зменяцца: а) ціск газу; б) шчыльнасць газу; в) колькасць рэчыва ў пасудзіне?

Абазначым праз $E subscript straight K space equals space fraction numerator m subscript 0 open angle brackets v squared close angle brackets over denominator 2 end fraction$ сярэднюю кінетычную энергію паступальнага руху малекул. Тады асноўнае ўраўненне малекулярна-кінетычнай тэорыі прыме выгляд:

$p space equals space 2 over 3 n open angle brackets E subscript straight K close angle brackets$

(3.2)

З выразу (3.2) вынікае, што ціск ідэальнага газу залежыць ад сярэдняй кінетычнай энергіі паступальнага руху яго малекул і іх канцэнтрацыі.

Ад тэорыі да практыкі

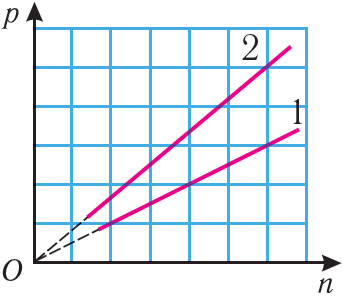
На малюнку 15 прыведзены графікі залежнасці ціску ад канцэнтрацыі для двух ідэальных газаў, тэмпературы якіх розныя. У колькі разоў адрозніваюцца сярэднія кінетычныя энергіі паступальнага руху малекул гэтых газаў?

1. Назавіце істотныя прыкметы паняцця «ідэальны газ».

2. Які механізм узнікнення ціску газу з пункту гледжання малекулярна-кінетычнай тэорыі?

3. Ад чаго залежыць ціск ідэальнага газу?

4. У табліцы прыведзены шчыльнасці газаў пры нармальных умовах:

Газ	вадарод	кісларод	азот	хлор
Шчыльнасць газу ρ, $Error converting from MathML to accessible text.$	0,090	1,43	1,25	3,21

У малекул якога газу сярэдняя квадратычная скорасць паступальнага руху максімальная?

5. У дзвюх пасудзінах знаходзяцца аднолькавыя колькасці малекул ідэальнага газу. У якім выпадку ціскі газу ў пасудзінах будуць аднолькавыя?

Адсылка да электроннага дадатку для павышанага ўзроўню

6. У балон, які змяшчае пэўную колькасць атамаў гелію, дадаюць такую ж колькасць малекул вадароду. Сярэдняя кінетычная энергія паступальнага руху малекул вадароду роўная сярэдняй кінетычнай энергіі цеплавога руху атамаў гелію. У колькі разоў зменіцца ціск газу ў балоне?

7. У цеплаізаляванай герметычна закрытай пасудзіне знаходзіцца ідэальны газ. Сярэдняя кінетычная энергія малекул газу пры ўдарах аб сценкі пасудзіны памяншаецца. Ці награваецца пасудзіна?

Прыклады рашэння задач

Прыклад 1. Балон электрычнай лямпы напоўнены газам, шчыльнасць якога $p$ . Пасля ўключэння лямпы ціск газу ў ёй павялічыўся ад $p subscript 1 space equals space 90 space кПа$ да $p subscript 2 space equals space 150 space кПа$ . Вызначце, на колькі пры гэтым павялічыўся сярэдні квадрат скорасці цеплавога руху малекул газу.

Дадзена:

straight rho space equals space 0 comma 90 space кг over straight м cubed

p subscript 1 space equals space 90 space кПа space equals space 9 comma 0 times 10 to the power of 4 space Па

p subscript 2 space equals space 150 space кПа space equals space 1 comma 50 times 10 to the power of 5 space Па

increment open angle brackets v squared close angle brackets space minus space ?

Рашэнне. Пакажам, што паміж шчыльнасцю ρ газу і канцэнтрацыяй n яго часціц існуе сувязь. Шчыльнасць рэчыва газу роўная адносінам масы да адведзенага яму аб’ёму. Паколькі здабытак масы адной малекулы m₀ і колькасці N малекул роўны масе рэчыва, то:

$straight rho space equals space m over V space equals space fraction numerator m subscript 0 N over denominator V end fraction space equals space m subscript 0 n$ .

Тады асноўнае ўраўненне малекулярна-кінетычнай тэорыі можна запісаць у выглядзе: $p space equals space 1 third straight rho open angle brackets v squared close angle brackets$ . Значыць, сярэдні квадрат скорасці цеплавога руху малекул газу $open angle brackets v squared close angle brackets space equals space fraction numerator 3 p over denominator straight rho end fraction$ . Вызначым змяненне сярэдняга квадрата скорасці цеплавога руху малекул газу пасля ўключэння лямпы:

$increment open angle brackets v squared close angle brackets space equals space fraction numerator 3 p subscript 2 over denominator straight rho end fraction minus fraction numerator 3 p subscript 1 over denominator straight rho end fraction space equals space 3 over straight rho left parenthesis p subscript 1 minus p subscript 2 right parenthesis$ .

$increment open angle brackets v squared close angle brackets space equals space fraction numerator 3 over denominator 0 comma 90 space begin display style кг over straight м cubed end style end fraction times left parenthesis 1 comma 50 times 10 to the power of 5 space Па minus 9 comma 0 times 10 to the power of 4 space Па right parenthesis space equals space 2 comma 0 times 10 to the power of 5 space straight м squared over straight с squared$ .

Адказ: $increment open angle brackets v squared close angle brackets space equals space 2 comma 0 times 10 to the power of 5 space straight м squared over straight с squared$ .

Прыклад 2. У пасудзіне ёмістасцю V = 10 л знаходзіцца аднаатамны газ, колькасць рэчыва якога ν = 2,0 моль і ціск p = 6,0 · 10₅ Па. Вызначце сярэднюю кінетычную энергію цеплавога руху атамаў гэтага газу.

Дадзена:

V space equals space 10 space straight л space equals space 1 comma 0 times 10 to the power of negative 2 end exponent space straight м cubed

p space equals space 6 comma 0 times 10 to the power of 5 space Па

nu space equals space 2 comma 0 space моль

open angle brackets E subscript straight K close angle brackets space minus space ?

Рашэнне. З асноўнага ўраўнення малекулярна-кінетычнай тэорыі, запісанага ў выглядзе $p space equals space 2 over 3 n open angle brackets E subscript straight K close angle brackets$ , вынікае, што $open angle brackets E subscript straight K close angle brackets space equals space fraction numerator 3 p over denominator 2 n end fraction$ . Паколькі канцэнтрацыя атамаў $n space equals space N over V$ , а колькасць атамаў газу

$N space equals space nu N subscript straight A$ , то $open angle brackets E subscript straight K close angle brackets space equals space fraction numerator 3 p over denominator 2 n end fraction space equals space fraction numerator 3 p V over denominator 2 N end fraction space equals space fraction numerator 3 p V over denominator 2 v N subscript straight A end fraction$ .

$open angle brackets E subscript straight K close angle brackets space equals space fraction numerator 3 times 6 comma 0 times 10 to the power of 5 space Па times 1 comma 0 times 10 to the power of negative 2 end exponent space straight м cubed over denominator 2 times 2 comma 0 space моль space times 6 comma 02 times 10 to the power of 23 space моль to the power of negative 1 end exponent end fraction space equals space 7 comma 5 times 10 to the power of negative 21 end exponent space Дж$ .

Адказ: $open angle brackets E subscript straight K close angle brackets space equals space 7 comma 5 times 10 to the power of negative 21 end exponent space Дж$ .

Практыкаванне 2

1. Вызначце канцэнтрацыю малекул кіслароду, калі сярэдняе значэнне квадрата скорасці іх цеплавога руху $open angle brackets v squared close angle brackets space equals space 4 comma 9 times 10 to the power of 5 space straight м squared over straight с squared$ , а ціск газу $p space equals space 2 comma 0 times 10 to the power of 5 space Па$ .

2. У адной з дзвюх аднолькавых пасудзін знаходзіцца кісларод, а ў другой — азот. Колькасць малекул кожнага газу і сярэднія значэнні квадратаў скорасцей іх цеплавога руху аднолькавыя. Вызначце ціск азоту, калі ціск кіслароду p₁ = 32 кПа.

3. Вызначце сярэднюю кінетычную энергію паступальнага руху малекул кіслароду пры нармальных умовах, калі іх канцэнтрацыя n = 2,7 · 10²⁵ м^–3.

4. У балоне ёмістасцю V = 4,0 л знаходзіцца N = 8,0 · 10²⁵ малекул азоту. Вызначце сярэднюю кінетычную энергію паступальнага руху малекул, калі ціск азоту p = 2,0 МПа.

5. У балоне ёмістасцю V = 2,5 м³ знаходзіцца гелій масай m = 3,0 кг. Вызначце сярэдняе значэнне квадрата скорасці цеплавога руху атамаў гелію, калі яго ціск p = 100 кПа.

6. У колькі разоў зменіцца ціск ідэальнага аднаатамнага газу, калі сярэдняя кінетычная энергія цеплавога руху яго атамаў павялічыцца ў α = 3 разы, а аб’ём газу паменшыцца ў β = 2 разы?

Адсылка да электроннага дадатку для павышанага ўзроўню

7. У пасудзіне знаходзіцца ідэальны газ, ціск і абсалютная тэмпература якога р₁ і Т₁ адпаведна. Вызначце, як і ў колькі разоў зменіцца ціск газу, калі сярэдняе значэнне квадрата скорасці цеплавога руху яго малекул павялічыцца на α = 10 %, а адведзены яму аб’ём паменшыцца на β = 50 %.

§ 3. Макра- і мікрапараметры. Ідэальны газ. Асноўнае ўраўненне малекулярна-кінетычнай тэорыі ідэальнага газу

Оглавление