§ 32-1. Вихревое электрическое поле. ЭДС индукции в движущихся проводниках
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 32-1. Вихревое электрическое поле. ЭДС индукции в движущихся проводниках |
| Напечатано:: | Гость |
| Дата: | Friday, 17 October 2025, 05:19 |
Вихревое электрическое поле. При изменении магнитного потока через поверхность, ограниченную проводящим замкнутым неподвижным (относительно выбранной инерциальной системы отсчёта) контуром, в нём возникает электрический ток. Это свидетельствует о том, что на свободные заряженные частицы в контуре действуют силы. Но для беспорядочно движущихся заряженных частиц усреднённое значение силы Лоренца равно нулю, следовательно, на такие частицы действует электрическое поле. Дж. Максвелл первым предположил, что при любом изменении во времени магнитного поля в окружающем пространстве возникает электрическое поле. Его называют индукционным или индуцированным. Именно это индукционное электрическое поле действует на заряженные частицы, приводя их в упорядоченное движение и создавая индукционный электрический ток. Подчеркнём, что индукционное электрическое поле не связано с электрическими зарядами, его источником является изменяющееся со временем магнитное поле. Линии напряжённости индукционного электрического поля замкнуты.
Электрическое поле, возникающее при любом изменении во времени магнитного поля, является одним из вихревых полей.
Вихревой, т. е. непотенциальный, характер индукционного электрического поля — причина того, что при перемещении заряда по замкнутой цепи это поле совершает работу, не равную нулю.
Таким образом, ЭДС индукции, возникающая в неподвижном замкнутом контуре, находящемся в изменяющемся во времени магнитном поле, равна работе сил вихревого электрического поля по перемещению вдоль этого контура единичного положительного заряда. Если такой контур оказывается проводящим, то возникшая в нём ЭДС индукции приводит к появлению индукционного тока.
Максвелл в 1873 г. установил, что ЭДС индукции, возникающая в неподвижном контуре при изменении во времени магнитного поля, не зависит от характеристик этого контура (вещества, вида свободных носителей заряда, сопротивления, температуры и др.). На основании этого он сделал вывод, что роль контура сводится только к индикации вихревого электрического поля, создаваемого переменным магнитным полем.
Итак, сущность явления электромагнитной индукции заключается в том, что вихревое электрическое поле возникает в любой точке пространства, если в этой точке существует изменяющееся во времени магнитное поле, независимо от того, есть там проводящий контур или нет.
Линии напряжённости вихревого электрического поля охватывают линии индукции изменяющегося во времени магнитного поля. Направление линий напряжённости вихревого электрического поля определяют по правилу Ленца. Действительно, если поместить в изменяющееся во времени магнитное поле замкнутый проводящий контур, то по нему в направлении линий напряжённости электрического поля пойдёт индукционный электрический ток.

Этот ток создаёт индукционное магнитное поле, индукция которого изображена на рисунке 184.2 штриховыми линиями. Она направлена так, что индукционное магнитное поле противодействует изменению основного магнитного поля (правило Ленца): если модуль индукции основного поля возрастает, то вектор
направлен противоположно вектору индукции основного поля
(см. рис. 184.2, а); если модуль индукции основного поля уменьшается, то векторы
и
одинаково направлены (см. рис. 184.2, б).
ЭДС индукции в движущихся проводниках. Рассмотрим металлический прямолинейный проводник длиной l, движущийся в неизменяющемся во времени магнитном поле так, что скорость его движения перпендикулярна индукции магнитного поля
а также проводнику. Проводник тоже перпендикулярен
(рис. 184.3, а). Несмотря на отсутствие вихревого электрического поля, в проводнике возникает ЭДС индукции. Выясним причину её возникновения.
Очевидно, что свободные электроны в проводнике движутся вместе с ним. В магнитном поле на движущиеся заряженные частицы действует сила Лоренца. Под действием этой силы свободные электроны перемещаются к торцу проводника (рис. 184.3, б). Это приводит к тому, что на одном конце проводника преимущественно накапливаются отрицательные заряды, а на другом — положительные, совместно создающие электрическое поле. Поэтому между концами проводника возникает разность потенциалов U.
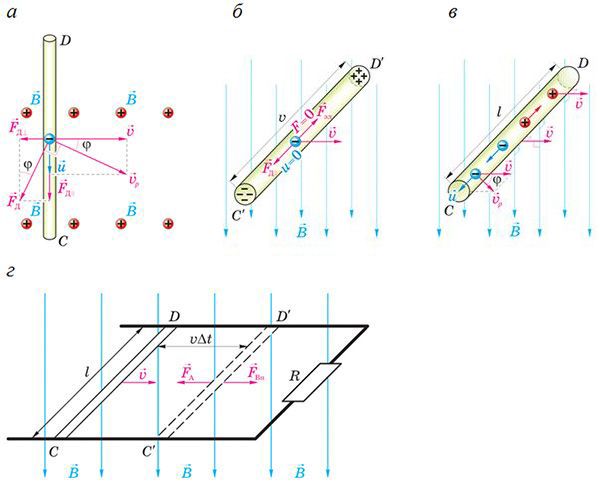
Пусть мгновенная скорость в начале упорядоченного движения электронов в системе отсчёта, связанной с проводником, равна как только проводник пересекает границу магнитного поля. Тогда мгновенная скорость
движения электронов в инерциальной системе отсчёта, в которой задано стационарное магнитное поле,
, причём направление скорости
составляет угол φ с направлением скорости
движения проводника (рис. 184.3, б). Если е — модуль заряда электрона, то модуль силы Лоренца, действующей на электрон со стороны магнитного поля, FЛ = еBυр, а её направление составляет угол 90° с направлением скорости
движения электрона.
На этом этапе движения свободных электронов сила Лоренца имеет две составляющие: , направленную перпендикулярно проводнику, и
, направленную вдоль проводника. Именно продольная составляющая силы Лоренца
выполняет работу по разделению зарядов. Её модуль
. Перераспределение зарядов внутри проводника, связанное с увеличением абсолютного значения избыточных зарядов на его торцах, происходит до тех пор, пока сила, действующая на свободный электрон со стороны нарастающего электрического поля, не скомпенсирует продольную составляющую силы Лоренца:
, или
(1). Поскольку напряжённость однородного электрического поля внутри прямолинейного проводника связана с разностью потенциалов между его концами соотношением
(2), то из уравнений (1) и (2) следует, что
. Таким образом, сторонней силой, способствующей разделению зарядов в проводнике, является продольная составляющая силы Лоренца
.
Магнитное поле способствует разделению электрических зарядов в движущемся проводнике, однако не может служить источником энергии, так как магнитная сила, действующая на движущиеся электрические заряды, перпендикулярна скорости заряда, поэтому работа магнитных сил всегда равна нулю. В изолированном проводнике, движущемся с постоянной скоростью в стационарном магнитном поле, возникшая при разделении зарядов электрическая сила компенсирует действие продольной составляющей силы Лоренца
и обращает в нуль скорость упорядоченного движения электронов
, следовательно, перпендикулярная составляющая силы Лоренца
тоже оказывается равной нулю.
Превращение механической энергии в электрическую принято рассматривать при наличии индукционного тока. Рассмотрим прямоугольный контур, образованный металлическим проводником длиной l, находящимся на гладких проводящих горизонтальных шинах в вертикальном однородном магнитном поле, модуль индукции которого В (рис. 177.2, г). Правые концы шин подсоединены к резистору, электрическое сопротивление которого R. Сопротивление остальной части контура пренебрежимо мало. Если проводник скользит с постоянной скоростью , направленной горизонтально и перпендикулярно проводнику, то за промежуток времени Δt площадь поверхности, ограниченной контуром, изменится на величину
, а магнитный поток через эту поверхность — на
. Следовательно, в контуре наводится ЭДС индукции
, обеспечивающая индукционный ток. Воспользовавшись законом Ома для полной цепи, выразим силу индукционного тока
.
Однородное магнитное поле на прямолинейный участок проводника с током действует силой Ампера, модуль которой . Обеспечить движение проводника с постоянной скоростью можно, если скомпенсировать силу Ампера
внешней силой
. Воспользовавшись правилом левой руки, можно убедиться, что направление силы Ампера
противоположно направлению скорости
движения проводника (см. рис. 184.3, г), что согласуется с правилом Ленца. Мощность, развиваемая внешней силой,
совпадает с мощностью индукционного тока.
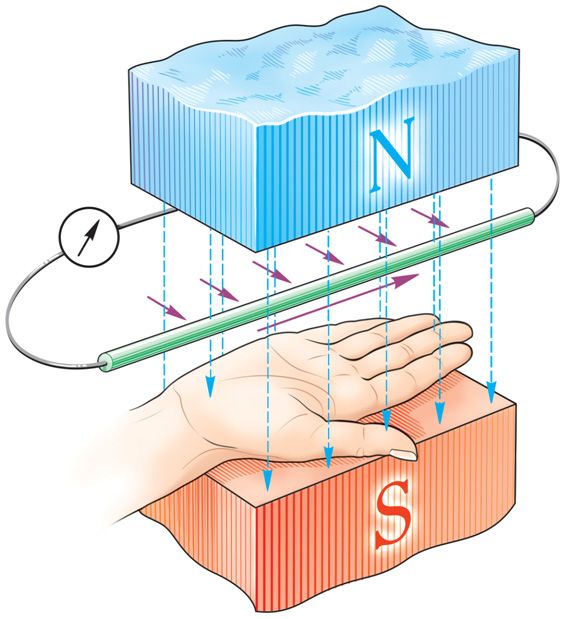
Направление индукционного тока можно определить по правилу правой руки: если правую руку расположить вдоль проводника так, чтобы перпендикулярная составляющая магнитной индукции входила в ладонь, а отогнутый большой палец показывал направление движения проводника, то четыре вытянутых пальца укажут направление индукционного тока в проводнике (рис. 184.4).
Если угол α между направлениями скорости движения проводника и индукции
магнитного поля не равен 90°, то ЭДС индукции, возникающая в прямолинейном проводнике, поступательно движущемся в однородном магнитном поле, прямо пропорциональна модулю индукции магнитного поля, длине активной части проводника (части, которая находится в магнитном поле), модулю скорости движения проводника и синусу угла между направлениями магнитной индукции поля и скорости проводника:

1. В чём отличие электростатического поля от вихревого электрического поля?
2. Что определяет ЭДС индукции, возникающую в прямолинейном проводнике, поступательно движущемся в стационарном магнитном поле?
3. От чего зависит ЭДС индукции, возникающая в прямолинейном проводнике, который поступательно движется в неизменяющемся со временем магнитном поле?
Прямолинейный проводник длиной l = 40 см перемещают поступательно в однородном магнитном поле, модуль индукции которого В = 0,16 Тл. Ось проводника составляет угол α = 30° с направлением линий индукции магнитного поля, а скорость движения перпендикулярна его оси и линиям индукции. Определите модуль ускорения проводника, если ЭДС индукции в проводнике увеличивается со скоростью .
l = 40 см = 0,40 м
В = 0,16 Тл
α = 30°
Решение: Модуль ускорения проводника . С учётом формулы
для определения ЭДС индукции, возникающей в проводнике, движущемся в однородном магнитном поле, запишем:
Отсюда модуль ускорения проводника .
Ответ: .
Упражнение 23.1
1. Самолёт с размахом крыльев l = 20 м летит горизонтально со скоростью, модуль которой υ = 900 . Определите разность потенциалов, возникающую между концами крыльев самолёта, если модуль вертикальной составляющей индукции магнитного поля Земли
= 5,0 · 10-5 Тл.
2. В проводнике, входящем в замкнутый проводящий контур и движущемся перпендикулярно линиям индукции магнитного поля (рис. 184.5), возник индукционный ток, направление которого показано на рисунке. Определите направление движения проводника.

3. Прямолинейный проводник длиной l = 20 см перемещают поступательно в однородном магнитном поле, модуль индукции которого В = 0,32 Тл. Ось проводника составляет угол α = 30° с направлением линий магнитной индукции, а скорость его движения перпендикулярна оси и линиям индукции. Определите скорость изменения ЭДС индукции в проводнике, если модуль ускорения проводника а = 2,5 .