§ 30. Сила Лоренца. Движение заряженных частиц в магнитном поле
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 30. Сила Лоренца. Движение заряженных частиц в магнитном поле |
| Напечатано:: | Гость |
| Дата: | Пятница, 4 Апрель 2025, 21:20 |
Поскольку электрический ток представляет собой упорядоченное движение заряженных частиц, то это означает, что магнитное поле, действуя на проводник с током, действует тем самым на каждую из этих частиц. Таким образом, силу Ампера можно рассматривать как результат сложения сил, действующих на отдельные движущиеся заряженные частицы. Как можно определить силу, действующую со стороны магнитного поля на заряженную частицу, движущуюся в этом поле?
Сила Лоренца. Силу, которой магнитное поле действует на заряженную частицу, движущуюся в этом поле, называют силой Лоренца в честь выдающегося нидерландского физика Хендрика Антона Лоренца (1853–1928).
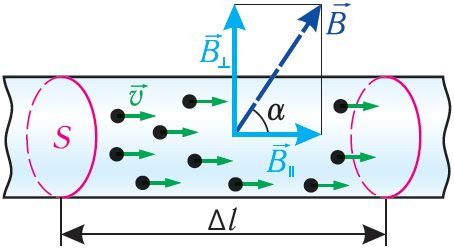
Модуль силы Лоренца можно определить по формуле , где N — общее число свободных заряженных одинаковых частиц на прямолинейном участке проводника длиной Δl (рис. 167). Если модуль заряда одной частицы q, а модуль суммарного заряда всех частиц Nq, то согласно определению силы тока
, где Δt — промежуток времени, за который заряженная частица проходит участок проводника длиной Δl. Тогда
Поскольку – модуль средней скорости упорядоченного движения заряженной частицы в стационарном* электрическом поле внутри проводника, то формулу для определения модуля силы Лоренца можно записать в виде:
(30.1)
где α — угол между направлениями индукции магнитного поля и скорости
упорядоченного движения заряженной частицы.
Из формулы (30.1) следует, что сила Лоренца максимальна в случае, когда заряженная частица движется перпендикулярно направлению индукции магнитного поля (α = 90°). Когда частица движется вдоль линии индукции поля (α = 0° или α = 180°), сила Лоренца на неё не действует. Сила Лоренца зависит от выбора инерциальной системы отсчёта, так как в разных системах отсчёта скорость движения заряженной частицы может отличаться.
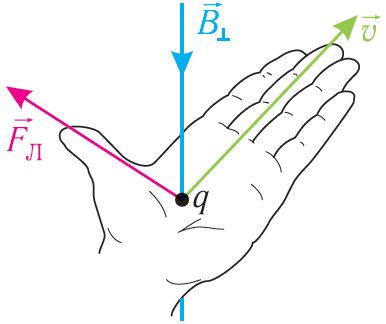
Направление силы Лоренца, действующей на заряженную частицу, как и направление силы Ампера, определяют по правилу левой руки (рис. 168): если левую руку расположить так, чтобы составляющая индукции магнитного поля, перпендикулярная скорости движения частицы, входила в ладонь, а четыре пальца были направлены по движению положительно заряженной частицы (против движения отрицательно заряженной частицы), то отогнутый на 90° в плоскости ладони большой палец укажет направление действующей на частицу силы Лоренца.
Сила Лоренца перпендикулярна как направлению скорости движения частицы, так и направлению индукции
магнитного поля.
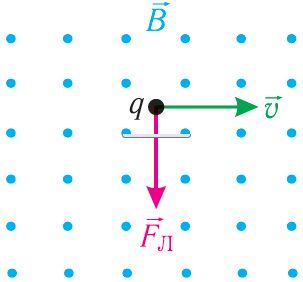
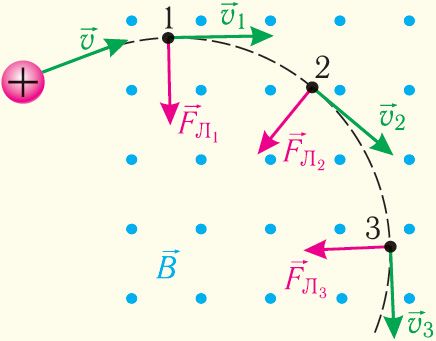
На рисунке 169 представлены направления индукции магнитного поля, скорости
движения частицы в данный момент времени и силы Лоренца
, действующей на частицу со стороны магнитного поля. Определите знак заряда частицы.
* Электрическое поле, создаваемое и поддерживаемое источником тока в течение длительного промежутка времени и обеспечивающее постоянный электрический ток в проводнике, называют стационарным электрическим полем. ↑
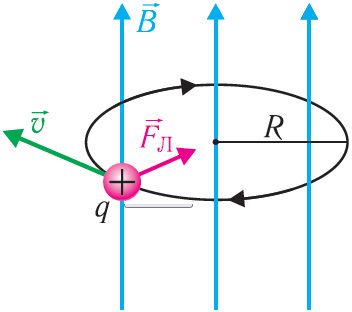
Движение заряженных частиц в однородном магнитном поле. Под действием силы Лоренца частицы, имеющие электрический заряд, движутся в магнитном поле по криволинейным траекториям. Причём если в данной инерциальной системе отсчёта направление скорости движения частицы перпендикулярно направлению индукции однородного магнитного поля (,
), то траекторией движения заряженной частицы является окружность (рис. 170).
Пусть в однородном магнитном поле, индукция которого , движется частица со скоростью
, направленной перпендикулярно линиям индукции. Масса частицы m и заряд q. Так как сила Лоренца
перпендикулярна скорости
движения частицы (см. рис. 170), то эта сила изменяет только направление скорости, сообщая частице центростремительное ускорение, модуль которого согласно второму закону Ньютона:
В результате частица движется по окружности, радиус которой можно определить из формулы :
Период Т обращения частицы, движущейся по окружности в однородном магнитном поле:
(30.2)
Как следует из выражения (30.2), период обращения частицы не зависит от модуля скорости её движения и радиуса траектории, а определяется только модулем заряда частицы, её массой и значением индукции магнитного поля.
В однородном магнитном поле, модуль индукции которого В = 4,0 мТл, перпендикулярно линиям индукции поля движется электрон. Чему равен модуль ускорения электрона, если модуль скорости его движения ? Масса и модуль заряда электрона mе = 9,1 · 10–31 кг и е = 1,6 · 10–19 Кл соответственно.
![]()
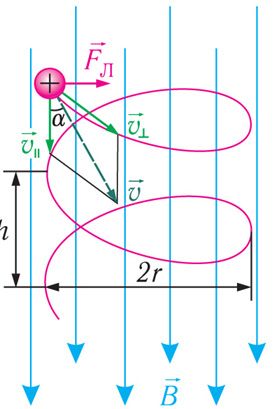
Если заряженная частица движется в однородном магнитном поле так, что направление её скорости образует с направлением индукции магнитного поля
угол α, причём α ≠ 0, α ≠ π, то траектория движения частицы представляет собой винтовую линию (рис. 170.1). При этом радиус R винтовой линии зависит от модуля составляющей скорости
, перпендикулярной индукции магнитного поля, а шаг винтовой линии h — от модуля составляющей скорости
, параллельной магнитной индукции. Таким образом, траектория движения заряженной частицы как бы навивается на линии магнитной индукции.
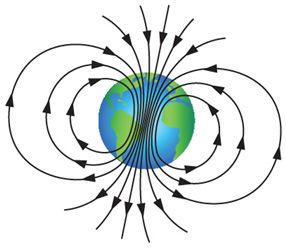
Подобное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Движущиеся с огромными скоростями заряженные частицы из космоса захватываются магнитным полем Земли и образуют так называемые радиационные пояса (рис. 170.2), в которых частицы перемещаются по винтообразным траекториям между северным и южным магнитными полюсами туда и обратно за промежуток времени порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния (рис. 170.3).
Если заряженная частица в момент возникновения внешнего электрического поля покоилась, то , где U — напряжение между точками, в которых находилась частица в моменты возникновения внешнего электрического поля и выхода из него, q — модуль заряда частицы. Поэтому модуль скорости частицы при выходе из электрического поля:
Если после этого частица попадает в однородное магнитное поле, индукция которого перпендикулярна направлению её скорости, то радиус окружности, по дуге которой будет двигаться частица,
, откуда
Величину называют удельным зарядом частицы. Поэтому если опытным путём определить радиус траектории движения частицы в магнитном поле, то, зная индукцию магнитного поля и ускоряющее напряжение электрического поля, можно рассчитать удельный заряд частицы. Этот метод используют при конструировании приборов, которые называют масс–спектрометрами.
Интересно знать
Поскольку сила Лоренца направлена под углом 90° к скорости движения заряженной частицы в каждой точке траектории (рис. 171), то работа этой силы при движении заряженной частицы в магнитном поле равна нулю. Поэтому кинетическая энергия частицы, движущейся в стационарном (не изменяющемся во времени) магнитном поле, не изменяется, т. е. стационарное магнитное поле нельзя использовать для ускорения заряженных частиц.
Увеличение кинетической энергии частицы, т. е. её разгон, возможно под действием электрического поля (в этом случае изменение кинетической энергии частицы равно работе силы поля). Поэтому в современных ускорителях (рис. 172) заряженных частиц электрическое поле используют для ускорения, а магнитное — для «формирования» траектории движения заряженных частиц.

1. Как определить модуль силы, действующей со стороны магнитного поля на движущуюся в нём заряженную частицу?
2. Как определяют направление силы Лоренца?
3. Заряженная частица движется в однородном магнитном поле со скоростью, направленной перпендикулярно линиям индукции. По какой траектории движется частица?
4. От чего зависит период обращения заряженной частицы в однородном магнитном поле?
![]()
5. Почему сила Лоренца изменяет направление скорости движения частицы, но не влияет на её модуль?
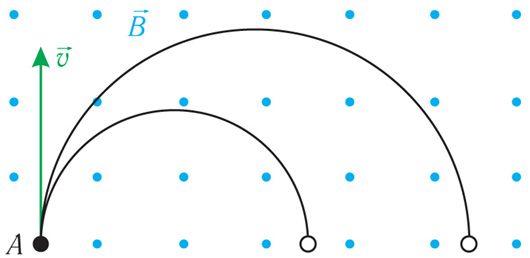
6. На рисунке 172.1 представлены траектории движения двух частиц, имеющих одинаковые заряды. Частицы влетают в однородное магнитное поле из одной точки А с одинаковыми скоростями. Определите знак заряда частиц. Объясните причину несовпадения траекторий их движения.
Пример 1. Электрон движется в однородном магнитном поле по окружности радиусом R = 12 см со скоростью, модуль которой значительно меньше модуля скорости света. Определите модуль импульса электрона, если модуль индукции магнитного поля В = 0,020 Тл.
R = 12 см = 0,12 м
В = 0,020 Тл
Решение: По определению модуль импульса электрона p = mv, где m — масса электрона; v — модуль скорости его движения.
На электрон в магнитном поле действуют сила Лоренца и сила тяжести, модуль которой во много раз меньше модуля силы Лоренца. Поэтому действием силы тяжести на движущуюся в магнитном поле заряженную частицу можно пренебречь. Согласно второму закону Ньютона , откуда
, где е = 1,6 · 10–19 Кл — модуль заряда электрона.
Следовательно, .
Ответ: .
![]()
Пример 2. Электрон, ускоренный из состояния покоя в электростатическом поле разностью потенциалов U = 270 В, движется параллельно тонкому длинному прямолинейному проводнику, находящемуся в вакууме, на расстоянии r = 5,0 мм от него. Определите модуль силы, которая начнёт действовать на электрон, если по проводнику пустить электрический ток, а также радиус кривизны его траектории в начале искривлённого участка при силе тока в проводнике I = 10 А.
U = 270 В
r = 5,0 мм = 5,0 · 10–3 м
I = 10 А
R — ?
Решение: Модуль скорости движения электрона, ускоренного из состояния покоя в электростатическом поле разностью потенциалов U, можно определить, воспользовавшись формулой (2) . Модуль индукции магнитного поля, образованного тонким длинным прямолинейным проводником, если по нему пропустить электрический ток I:
.
Тогда, воспользовавшись формулой (1), можно определить модуль силы Лоренца:
Как только появляется магнитное поле, создаваемое проводником с током, на электрон начинает действовать сила Лоренца, и электрон продолжает двигаться, но уже с центростремительным ускорением: . Тогда
, откуда
.
Ответ: Fл = 6,2 · 10−16 Н, R = 0,14 м.
Упражнение 22
1. Электрон движется со скоростью, модуль которой , перпендикулярно линиям индукции однородного магнитного поля, модуль индукции которого В = 1,6 мТл. Определите модуль силы, действующей на электрон в магнитном поле.
2. Электрон движется в однородном магнитном поле по окружности, радиус которой R = 8,0 мм. Определите модуль индукции магнитного поля, если модуль скорости движения электрона . Масса электрона mе = 9,1 · 10–31 кг.
3. Пылинка движется в однородном магнитном поле, модуль индукции которого В = 1,0 Тл, перпендикулярно линиям индукции. Масса и заряд пылинки m = 0,80 мг и q = 1,6 нКл соответственно. Определите период обращения пылинки.
4. Электрон движется в однородном магнитном поле, модуль индукции которого В = 2,0 мТл, по окружности радиусом R = 2,0 см. Определите кинетическую энергию электрона. Масса электрона mе = 9,1 · 10–31 кг.
5. Определите, какую ускоряющую разность потенциалов должна пройти из состояния покоя частица, чтобы в однородном магнитном поле, модуль индукции которого В = 80 мТл, на неё действовала сила Лоренца, модуль которой F = 20 мкН. Масса частицы m = 12 мг, её заряд q = 3,0 мкКл. В магнитное поле частица влетает перпендикулярно линиям индукции.
![]()
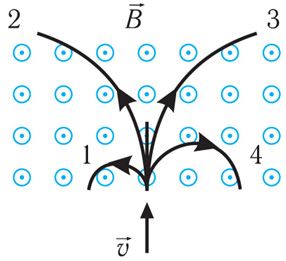
6. В однородное магнитное поле влетают частицы с зарядами, модули которых одинаковые (рис. 172.2). Выберите два верных утверждения.
1) Траектория 1 принадлежит отрицательно заряженной частице с наименьшей кинетической энергией.
2) Траектория 2 принадлежит положительно заряженной частице с наименьшей кинетической энергией.
3) Траектория 3 принадлежит положительно заряженной частице с наибольшей кинетической энергией.
4) Траектория 4 принадлежит отрицательно заряженной частице с наибольшей кинетической энергией.
5) Знаки зарядов всех частиц одинаковые.
7. Заряженная частица движется в пространстве с однородными электрическим и магнитным полями, линии напряжённости и магнитной индукции которых взаимно перпендикулярны. Модули напряжённости электрического поля и индукции магнитного соответственно Е = 0,24 и В = 0,04 Тл. Определите модуль скорости равномерного движения заряженной частицы. Действием силы тяжести на частицу пренебречь.