§ 21. Работа силы однородного электростатического поля. Потенциал
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 21. Работа силы однородного электростатического поля. Потенциал |
| Напечатано:: | Гость |
| Дата: | Thursday, 4 December 2025, 04:56 |
Электростатическое поле, действуя на находящиеся в нём заряды с определённой силой, может их перемещать. Вы знаете, что при перемещении тела действующая на него сила совершает работу. Выясним, от чего зависит работа силы по перемещению электрического заряда в электростатическом поле.
Работа силы однородного электростатического поля. Расчёты и результаты экспериментов доказали, что работа силы электростатического поля при перемещении заряда между двумя точками зависит только от положения этих точек и не зависит от вида траектории. Такой же особенностью, как вы знаете, обладает и гравитационное поле. Физические поля, работа сил которых не зависит от формы траектории, называют потенциальными.
![]()
Покажем, что электростатическое поле потенциально.
Пусть положительный пробный заряд q0 перемещают в однородном электростатическом поле напряжённостью из точки В в точку С вдоль линии напряжённости рассматриваемого поля (рис. 114, а). При этом сила
, которой поле действует на заряд q0, совершает работу. В скалярном виде выражение для работы имеет вид A = FΔrcosα, где α — угол между направлениями силы
и перемещения
заряда. Модуль электрической силы F = q0E, cosα = 1 (направления силы и перемещения заряда совпадают), а Δr = d, где d — расстояние между точками В и С. Тогда работа силы однородного электростатического поля по перемещению заряда:
AВС = q0Ed.
(21.1)

Если заряд перемещают по прямой из точки В в точку D под углом α к направлению напряжённости поля (рис. 114, б), то Δrcosα = d. Работа силы поля по перемещению заряда и в этом случае:
ABD = FΔrcosα = q0Ed.
Очевидно, что для перемещения заряда в обратном направлении (из точки D в точку В) внешней силе требуется, преодолевая силу поля, совершить работу, минимальное значение которой будет таким же: , поэтому ABD = ‒ADB. Следовательно, когда заряд возвращается в начальную точку, т. е. при движении заряда по замкнутой траектории, работа силы поля равна
нулю.
Предположим, что перемещение заряда q0 из точки В в точку D происходит в однородном электростатическом поле напряжённостью по криволинейной траектории (рис. 114, в). В этом случае траекторию можно разбить на такие малые участки, чтобы каждый из них можно было считать прямолинейным. Если просуммировать работы силы на каждом из этих участков, то получим:
AВD = q0E(Δd1 + Δd2 + … + Δdi + … + Δdn) = q0Ed,
где Δdi = Δricosα, Δri — модуль перемещения на i-м малом участке траектории, αi — угол между направлениями перемещения и напряжённости
поля (i = 1, 2, 3, …, n).
Таким образом, работа силы однородного электростатического поля по перемещению заряда из одной точки поля в другую не зависит от формы траектории, т. е. однородное электростатическое поле потенциально.

Какую работу совершит сила однородного электростатического поля, модуль напряжённости которого , при перемещении заряда q = 2,4 нКл по отрезку прямой (рис. 115), соединяющему точки: а) В и С; б) С и D; в) D и В?
Какую работу совершит сила поля при перемещении заряда по замкнутой траектории BCDB?
![]()

Потенциальная энергия заряда в электростатическом поле. Воспользовавшись законом сохранения энергии, можно показать, что любое электростатическое поле является потенциальным. Это означает, что электростатическое и гравитационное поля имеют похожие свойства, определяемые их потенциальным характером. Применительно к электростатическому полю эти свойства выражаются в следующем:
а) точечный электрический заряд, находящийся в любой точке электростатического поля, обладает потенциальной энергией взаимодействия с этим полем. Значение этой энергии определяют относительно произвольно выбираемой нулевой точки. В нулевой точке потенциальную энергию заряда принимают равной нулю. Потенциальная энергия взаимодействия точечного заряда с электростатическим полем равна работе, которую совершила бы сила поля при перемещении данного заряда из указанной точки поля в нулевую точку;
б) работа силы поля по перемещению электрического заряда q из точки 1 в точку 2 (рис. 116) может служить мерой изменения потенциальной энергии этого заряда в поле, созданном зарядом Q.
Пусть Wп1 и Wп2 — потенциальные энергии перемещаемого заряда в точках 1 и 2 электростатического поля. Тогда работа силы поля
A12 = –ΔWп12 = –(Wп2 – Wп1),
(21.2)
где ΔWп12 — приращение потенциальной энергии заряда q при его перемещении из точки 1 в точку 2.
Перепишем выражение (21.2) в виде
A12 = Wп1 – Wп2
(21.3)
и проанализируем его, когда на заряд q действует только сила со стороны электростатического поля:
1) если работа силы поля A12 > 0 (перемещение положительного заряда q происходит в направлении линий напряжённости поля), то потенциальная энергия заряда уменьшается: ΔWп12 < 0. При этом, согласно закону сохранения энергии, увеличивается кинетическая энергия тела c зарядом q: ;
2) если работа силы поля A12 < 0 (перемещение положительного заряда противоположно направлению линий напряжённости поля), то потенциальная энергия заряда увеличивается: ΔWп12 > 0. При этом кинетическая энергия заряженного тела уменьшается: ;
3) если работа силы поля A12 = 0 (перемещение заряда перпендикулярно направлению линий напряжённости поля), то потенциальная энергия заряда не изменяется.
![]()
Следует подчеркнуть, что потенциальная энергия — это энергия взаимодействия, и её необходимо относить не к заряженной частице или телу, а к системе в целом. В частности, для заряженной частицы (тела), находящейся в электростатическом поле, это потенциальная энергия взаимодействия заряженной частицы с полем, т. е. с другими заряженными частицами и (или) телами, являющимися источниками этого поля. Кратко это принято формулировать так: потенциальная энергия заряда в поле.
В каком случае (см. рис. 115) при перемещении положительного (отрицательного) заряда между двумя точками поля потенциальная энергия этого заряда: а) увеличивается; б) уменьшается; в) не изменяется?
Потенциал электростатического поля как его энергетическая характеристика. Из выражений (21.1) и (21.2) следует, что потенциальная энергия пробного заряда q0 в данной точке поля пропорциональна величине этого заряда. Следовательно, отношение не зависит от заряда и является энергетической характеристикой электростатического поля, получившей название потенциал.
Потенциал электростатического поля в данной точке пространства — физическая скалярная величина, равная отношению потенциальной энергии пробного заряда, помещённого в данную точку поля, к значению этого заряда:
(21.4)
За единицу потенциала в СИ принят вольт (В). Единица названа в честь итальянского учёного Алессандро Вольта (1745–1827), внёсшего большой вклад в изучение электрических явлений. 1 В — потенциал такой точки электростатического поля, в которой заряд 1 Кл обладал бы потенциальной энергией 1 Дж.
Потенциал φ электростатического поля точечного заряда Q на расстоянии r от него в вакууме или в воздухе определяют соотношением
(21.5)
Знак заряда-источника поля определяет знак потенциала этого поля.
![]()
Поскольку потенциальная энергия заряда в электростатическом поле зависит от выбора нулевой точки, то эта зависимость сохраняется и для потенциала. Если принять, что на бесконечно большом расстоянии от источника поле отсутствует, т. е. потенциальная энергия системы «заряд ‒ электростатическое поле» на бесконечности равна нулю, то потенциал поля в данной точке можно определить следующим образом:
Если электрическое поле создано в однородной среде с диэлектрической проницаемостью ε, то потенциал поля
Следует отметить, что потенциал поля, создаваемого положительным зарядом, уменьшается по мере удаления от заряда, а потенциал поля, создаваемого отрицательным зарядом, увеличивается.
Из формулы (21.5) следует, что во всех точках поля, находящихся на расстоянии r от точечного заряда Q, потенциал φ одинаковый. Эти точки расположены на поверхности сферы радиусом R, центр которой находится в той же точке, что и заряд Q.
Потенциал поля, создаваемого равномерно заряженной сферой радиусом R, заряд которой Q, в вакууме в точках вне сферы на расстоянии r > R от её центра, определяют по формуле . В точках, находящихся на поверхности и внутри сферы по формуле
.
Электростатическое поле создано точечным неподвижным зарядом Q. Потенциал поля в точке, расположенной от заряда Q на расстоянии r = 27 см, φ = 80 В. В эту точку помещают пробный заряд q0. Определите: а) значение заряда, создающего поле; б) значение пробного заряда, если его потенциальная энергия в данной точке поля Wп = –0,8 мкДж.
![]()
Потенциал является скалярной величиной. Поэтому, если в данной точке пространства электростатическое поле создано системой точечных зарядов, то потенциал результирующего поля в этой точке равен алгебраической сумме потенциалов полей в этой же точке пространства, создаваемых каждым из точечных зарядов системы в отдельности:
φ = φ1 + φ2 + φ3 + … + φn,
т. е. для потенциала выполняется принцип суперпозиции.
Геометрическое место точек в электростатическом поле, потенциалы которых одинаковы, называют эквипотенциальной поверхностью.
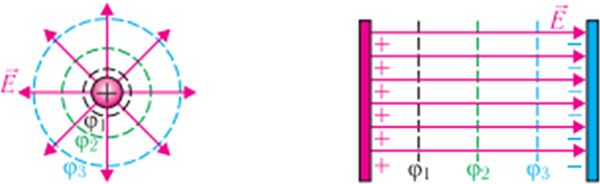
Используя эквипотенциальные поверхности, можно представлять графически электростатические поля. Через каждую точку поля проходят только одна линия напряжённости и одна эквипотенциальная поверхность. В каждой точке электростатического поля линия напряжённости и эквипотенциальная поверхность взаимно перпендикулярны (рис. 116.1). Представление электростатического поля с помощью эквипотенциальных поверхностей, как и термин «потенциал», ввёл немецкий учёный К. Ф. Гаусс в 1840 г.

![]()
1. Как определить работу силы однородного электростатического поля по перемещению электрического заряда?
2. Как вы понимаете утверждение «электростатическое поле потенциально»? Как связана работа силы электростатического поля по перемещению электрического заряда с изменением потенциальной энергии заряда в этом поле?
3. Какие две физические величины характеризуют электростатическое поле в любой его точке?
4. Что называют потенциалом электростатического поля?
5. Чему равен потенциал электростатического поля точечного заряда Q на расстоянии r от него?
6. Как определить потенциал электростатического поля, созданного несколькими точечными зарядами?
![]()
7. Докажите, что работа силы электростатического поля по перемещению заряда по замкнутой траектории равна нулю.
8. В чём проявляется сходство электростатического и гравитационного полей?
9. Положительно заряженная частица перемещается под действием только сил электростатического поля на некоторое расстояние. В какой точке траектории движения частицы — начальной или конечной — потенциал поля выше, если модуль её скорости: а) возрастает; б) убывает?
10. Отрицательно заряженная частица перемещается из состояния покоя под действием только сил электростатического поля на некоторое расстояние. В какой точке траектории движения частицы — начальной или конечной — потенциал поля выше?
11. Чему равен потенциал электростатического поля равномерно заряженной сферы радиусом R на расстоянии r от её центра, если: а) r ≤ R; б) r > R, а заряд сферы Q?
Пример 1. Электростатическое поле создано неподвижным точечным зарядом Q. В точке, находящейся на расстоянии r = 80 см от заряда, потенциал поля φ = 0,42 кВ. Определите модуль силы, действующей со стороны поля на точечный заряд q = 1,5 нКл, помещённый в эту точку.
r = 80 см = 0,80 м
φ = 0,42 кВ = 4,2 · 102 В
q = 1,5 нКл = 1,5 · 10–9 Кл
Решение: Модуль силы, которой электростатическое поле заряда Q действует на заряд q2, можно определить, воспользовавшись законом Кулона:
(1)
Из формулы (21.5) для потенциала поля точечного заряда найдём значение заряда:
(2)
Подставив выражение (2) в формулу (1), получим:
Ответ: F = 7,9 · 10–7 Н.
![]()
Пример 2. Электрон, двигаясь со скоростью, модуль которой , попадает в однородное электростатическое поле, направление линий напряжённости которого совпадает с направлением его скорости. Пройдя расстояние d = 2,0 см, электрон начинает двигаться в обратном направлении. Определите модуль напряжённости электростатического поля. Как изменилась потенциальная энергия взаимодействия электрона с полем к моменту перемены направления движения? Масса электрона mе = 9,1 · 10−31 кг.
d = 2,0 см = 2,0 · 10−2 м
е = ‒1,6 · 10–19 Кл
mе = 9,1 · 10−31 кг
ΔWп — ?
Решение: До изменения направления движения сила однородного электростатического поля совершает отрицательную работу по торможению электрона: .
Эту работу также можно определить по формуле А = eEd.
Значит: . Тогда
.
Согласно закону сохранения энергии полная энергия системы «электрон ‒ поле» остаётся неизменной, т. е. ΔWп + ΔWк = 0. Следовательно,
т. е. потенциальная энергия электрона возрастает на величину
Ответ: Е = 23 , ΔWп = 7,3 · 10–20 Дж.
Пример 3. В центре сферы с равномерно распределённым положительным зарядом Q1 = 36 нКл находится маленький шарик с отрицательным зарядом, модуль которого = 16 нКл. Определите потенциал электростатического поля в точке, находящейся вне сферы на расстоянии r = 10 м от её центра.
Q1 = 36 нКл = 3,6 · 10–8 Кл
Q2 = −16 нКл = −1,6 · 10–8 Кл
r = 10 м
Решение: Потенциал в искомой точке определим по принципу суперпозиции: φ = φ1 + φ2, где φ1 > 0 — потенциал электростатического поля положительно заряженной сферы, а φ2 < 0 — потенциал электростатического поля отрицательно заряженного шарика. Поскольку ,
, то
.
Ответ: φ = 18 В.
Упражнение 15

1. Зависит ли работа силы электростатического поля от траектории движения заряда? Сравните работу силы электростатического поля, образованного заряженными пластинами, при перемещении заряда q по контуру А и контуру В (рис. 117).
2. Отрицательный заряд, модуль которого |q| = 0,50 мкКл, переместили в однородном электростатическом поле на расстояние d = 10 см в направлении линий напряжённости. Определите работу силы поля, совершённую при перемещении заряда, и изменение потенциальной энергии взаимодействия заряда с полем, если модуль его напряжённости .
3. Точечный заряд q = 5,0 нКл перемещают в однородном электростатическом поле, модуль напряжённости которого . Перемещение, модуль которого Δr = 8,0 см, образует угол α = 60° с направлением линий напряжённости поля. Определите работу силы поля, изменения потенциальной и кинетической энергий заряда, если внешняя сила обеспечивает только прямолинейность перемещения заряда.
4. Работа, совершённая силой электростатического поля при переносе заряда q = 2,4 нКл из бесконечности в некоторую точку поля, А = 72 нДж. Определите потенциал этой точки поля. Что изменится, если работу по переносу первоначально неподвижного заряда совершает внешняя сила против силы электростатического поля? Минимальное значение работы внешней силы Авнеш = 72 нДж.
5. Модули напряжённости двух точек поля, создаваемого неподвижным точечным зарядом, отличаются в α = 9 раз. Определите, во сколько раз отличаются потенциалы этих точек поля.
6. Электростатическое поле создано находящимися на расстоянии r = 80 см друг от друга двумя разноимёнными точечными зарядами, модули которых |Q1| = |Q2| = 6,4 нКл. Определите модуль напряжённости и потенциал в точке пространства, находящейся на середине отрезка, соединяющего эти заряды.
![]()
7. Уединённая заряженная металлическая сфера радиусом R = 20 см подвешена на неокрашенной шёлковой нити в воздухе. Определите, во сколько раз потенциал электростатического поля положительного заряда сферы в точке, находящейся на расстоянии r1 = 4,0 см от центра сферы, больше потенциала поля заряда сферы в точке, находящейся на расстоянии l = 10 см от поверхности сферы.