§ 6. Изотермический, изобарный и изохорный процессы
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 6. Изотермический, изобарный и изохорный процессы |
| Напечатано:: | Гость |
| Дата: | Пятница, 29 Ноябрь 2024, 20:43 |
Свойство газов существенно изменять предоставленный им объём широко используют в тепловых двигателях. Анализируя процессы, происходящие с газом в этих устройствах, важно знать, каким законам подчиняются газы и каковы условия применимости этих законов.
Процессы в газах часто происходят так, что изменяются только два параметра из пяти (p, V, T, m, M). Если при постоянных массе и молярной массе ещё один из макропараметров (p, V, T), входящих в уравнение состояния идеального газа, не изменяется, то такие процессы называют изопроцессами.
Изотермический процесс. Процесс изменения состояния физической системы при постоянной температуре (T = const) называют изотермическим.
Если при переходе из начального состояния в конечное масса и молярная масса идеального газа не изменяются, то из уравнения Клапейрона–Менделеева следует:
, или
, т. е.
.
(6.1)
Давление данной массы газа при постоянных молярной массе и температуре обратно пропорционально его объёму.
Это утверждение называют законом Бойля–Мариотта.
Справедливость закона Бойля–Мариотта можно продемонстрировать экспериментально, используя установку, представленную на рисунке 18 в § 5.
Если медленно изменять объём газа, находящегося в сосуде, то вследствие теплообмена с окружающей средой можно поддерживать температуру газа в сосуде практически постоянной. При этом уменьшение объёма газа при вращении винта 3 повлечёт за собой увеличение его давления и некоторое незначительное увеличение температуры. И наоборот, увеличение объёма приведёт к уменьшению давления и некоторому незначительному уменьшению температуры газа*.
1. Почему пузырьки воздуха, находящиеся в жидкости, поднимаясь вверх, увеличиваются в объёме?
2. Если, не отрываясь, выпить из пластиковой бутылки газированную воду, то можно обнаружить, что бутылка деформируется. Почему?
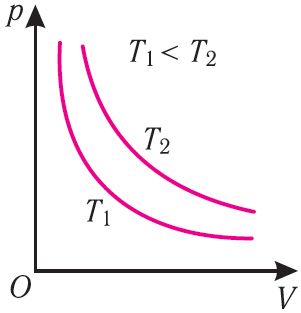
График изотермического процесса, совершаемого идеальным газом, в координатах (p, V) представляет собой гиперболу (рис. 22). В физике такую кривую называют изотермой. Разным значениям температуры газа соответствуют разные изотермы. Согласно соотношениям (6.1) для одинаковых объёмов газов с одинаковыми количествами вещества и разными температурами чем больше давление, тем выше температура (рис. 22).
Многочисленные опыты показали, что исследованные газы подчиняются закону Бойля–Мариотта тем точнее, чем меньше их плотность. При значительном увеличении давления газа этот закон перестаёт выполняться.
Изобразите графики изотермического процесса в координатах (p, T) и (V, T).
Интересно знать
Лёгкие расположены в грудной клетке, объём которой при дыхании периодически изменяется благодаря работе межрёберных мышц и диафрагмы. К огда грудная клетка расширяется, давление воздуха в лёгких становится меньше атмосферного, и воздух через воздухоносные пути устремляется в лёгкие — происходит вдох. При выдохе объём грудной клетки уменьшается, что вызывает уменьшение объёма лёгких. Давление воздуха в них становится выше атмосферного, и воздух из лёгких устремляется в окружающую среду.
* Незначительное изменение температуры газа принципиально необходимо для теплообмена с термостатом — передача тепла возможна только при разных температурах тел. ↑
Изобарный процесс. Процесс изменения состояния газа при постоянном давлении (p = const) называют изобарным.
В 1802 г. французский учёный Жозеф Гей-Люссак (1778–1850) рассмотрел этот процесс для воздуха, водорода, кислорода и азота.
Если при переходе из начального состояния в конечное масса и молярная масса газа не изменяются, то объём газа, как следует из уравнения Клапейрона–Менделеева:
или
, т. е.
.
(6.2)
Объём данной массы газа при постоянных молярной массе и давлении прямо пропорционален абсолютной температуре.
Это утверждение называют законом Гей-Люссака.
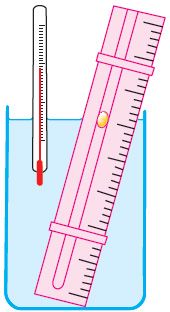
Справедливость закона Гей-Люссака можно продемонстрировать экспериментально, используя установку, представленную на рисунке 23. Жидкость в сосуде находится в тепловом равновесии с тонкой трубкой, заполненной воздухом, запертым капелькой масла. При увеличении температуры жидкости объём воздуха, находящегося в трубке под капелькой масла, возрастает и капелька движется вверх. При уменьшении температуры объём воздуха уменьшается — и капелька движется вниз.
Можно ли считать расширение газа при медленном нагревании его в цилиндре с подвижным поршнем изобарным процессом?
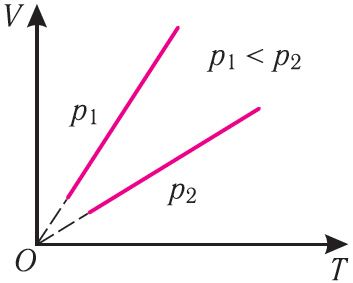
Поскольку V ~ T, то в координатах (V, T) график изобарного процесса, совершаемого идеальным газом, представляет собой прямую линию, продолжение которой проходит через начало координат (рис. 24). Эту линию называют изобарой.
Изобара реальных газов не может быть продлена до нулевого значения температуры (на графике пунктирная линия), потому что при низких температурах все газы существенно отличаются от модели «идеальный газ» и при дальнейшем уменьшении температуры превращаются в жидкости.
В одних и тех же координатах (V, T) можно построить несколько изобар, которые соответствуют разным давлениям данной массы идеального газа при неизменной молярной массе. Анализ соотношений (6.2) позволяет сделать вывод, что большему давлению соответствует меньший наклон изобары к оси температур (см. рис. 24).
Изобразите графики изобарного процесса в координатах (p, V) и (p, T).
Изохорный процесс. Процесс изменения состояния газа при постоянном объёме (V = const) называют изохорным.
Впервые этот процесс рассмотрел в 1787 г. французский учёный Жак Шарль (1746–1823)*.
Если при переходе из начального состояния в конечное масса и молярная масса идеального газа не изменяются, то давление газа, как следует из уравнения Клапейрона–Менделеева:
или
, т. е.
.
(6.3)
Давление данной массы газа при постоянных молярной массе и объёме прямо пропорционально абсолютной температуре.
Это утверждение называют законом Шарля.
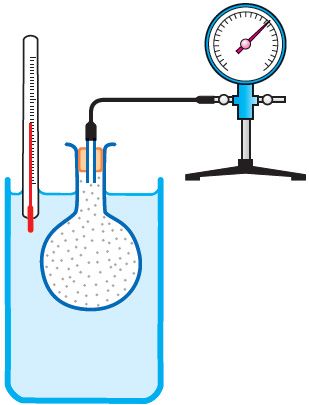
Справедливость закона Шарля можно продемонстрировать экспериментально, используя установку, представленную на рисунке 25. Колба, наполненная воздухом и соединённая с манометром, находится в тепловом равновесии с жидкостью в сосуде. При увеличении температуры жидкости давление воздуха в колбе возрастает, а при уменьшении температуры — давление воздуха уменьшается.
Идеальный газ определённой массы изохорно охлаждают так, что его температура уменьшается от t1 = 327 °С до t2 = 7 °С. Во сколько раз уменьшается давление газа?
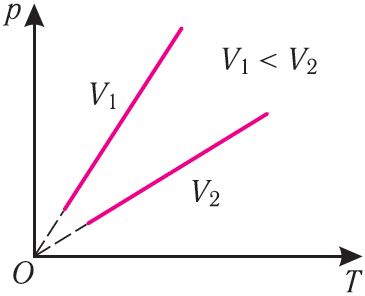
В координатах (p, T) график изохорного процесса, совершаемого идеальным газом, представляет собой прямую линию, продолжение которой проходит через начало координат (рис. 26). Эту линию называют изохорой.
Как и в случае изобарного процесса, изохора реальных газов не может быть продлена до нулевого значения температуры.
В одних и тех же координатах (p, T) можно построить несколько изохор, соответствующих разным объёмам данной массы газа при неизменной молярной массе. Анализ соотношений (6.3) показывает, что большему объёму соответствует меньший наклон изохоры к оси температур (см. рис. 26).
Изобразите графики изохорного процесса в координатах (p, V) и (V, T).
| Процесс изменения состояния идеального газа данной массы при неизменной молярной массе | |||
| изотермический | изобарный | изохорный | |
| При постоянном макроскопическом параметре | |||
| Уравнение процесса | |||
| Формулировка закона |
Давление данной массы идеального газа при неизменных молярной массе и температуре обратно пропорционально его объёму 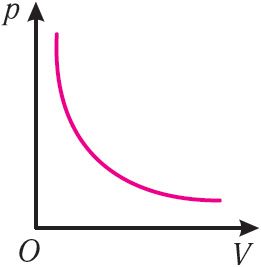 |
Объём данной массы идеального газа при неизменных молярной массе и давлении прямо пропорционален его абсолютной температуре 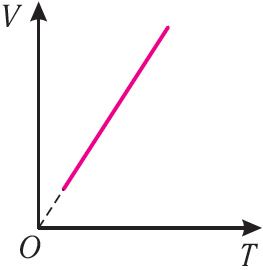 |
Давление данной массы идеального газа при неизменных молярной массе и объёме прямо пропорционально его абсолютной температуре 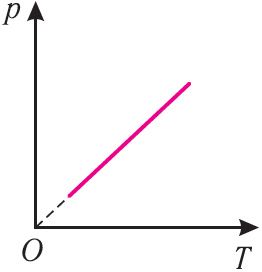 |
1. Как связаны давление и объём идеального газа при изотермическом процессе?
2. Как связаны объём и абсолютная температура идеального газа при изобарном процессе?
3. Как связаны давление и абсолютная температура идеального газа при изохорном процессе?
4. При выполнении каких условий справедлив каждый из законов изопроцессов в реальном газе?
5. Объём идеального газа определённой массы и неизменного химического состава изобарно увеличили в b = 1,5 раза, а затем давление газа изохорно уменьшили в c = 3 раза.
а) Как изменилась абсолютная температура газа в результате первого процесса?
б) Как изменилась абсолютная температура газа в результате второго процесса?
в) Во сколько раз начальная абсолютная температура газа отличается от его конечной температуры?
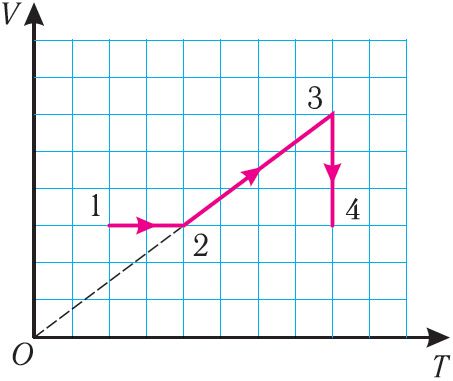
6. На рисунке 27 представлен график трёх процессов изменения состояния идеального газа определённой массы и неизменного химического состава.
а) Какому процессу соответствует участок 1 2 графика? Во сколько раз увеличилось давление газа в этом процессе?
б) Какому процессу соответствует участок 2 3 графика? Во сколько раз увеличились объём и абсолютная температура газа в этом процессе?
в) Какому процессу соответствует участок 3 4 графика? Как и во сколько раз изменились объём и давление газа в этом процессе?
г) Во сколько раз следует уменьшить температуру газа, чтобы изохорно перевести газ из состояния 4 в состояние 2?
* Несмотря на то что Шарль не опубликовал результаты своих исследований, история физики отдаёт приоритет открытия ему. ↑
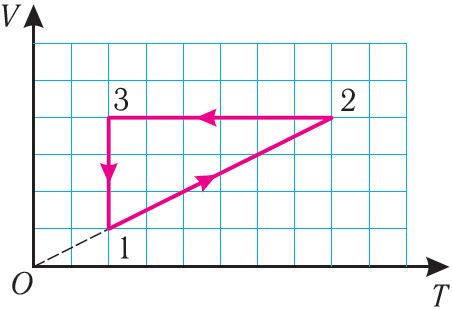
Пример 1. На рисунке 28 представлен график трёх процессов изменения состояния некоторой массы идеального газа. Как изменялись параметры газа на участках 1 2, 2
3, 3
1? Изобразите эти процессы в координатах (p, V) и (p, T).
Решение. На участке 1 2 объём газа прямо пропорционален абсолютной температуре, следовательно, процесс перехода газа из состояния 1 в состояние 2 является изобарным. Из графика следует, что в состоянии 2 температура и объём газа больше в 4 раза, чем в состоянии 1. Следовательно, в процессе изобарного расширения некоторой массы газа из состояния 1 в состояние 2 температура и объём газа увеличились. Это можно записать таким образом:
переход ,
,
,
,
происходит изобарное нагревание газа.
В процессе перехода газа из состояния 2 в состояние 3 остаётся постоянным объём (процесс изохорный), а температура газа уменьшается в 4 раза. Из соотношения (6.3) следует, что при изохорном охлаждении давление газа уменьшается пропорционально его абсолютной температуре. Поэтому можно записать:
переход ,
,
,
происходит изохорное охлаждение газа.
Процесс перехода газа из состояния 3 в состояние 1 — изотермический. При этом объём газа уменьшается в 4 раза, что влечёт за собой, согласно закону Бойля–Мариотта, увеличение давления газа в 4 раза:
переход ,
,
происходит изотермическое сжатие газа.
Опираясь на сделанные выводы, представим все три процесса в координатах (p, V) и (p, T) (рис. 29, а, б).
Пример 2. При изотермическом расширении идеального газа определённой массы его объём увеличился от V1 = 2,0 л до V2 = 5,0 л, а давление уменьшилось на Δp = –15 кПа. Определите первоначальное давление газа.
V1 = 2,0 л = 2,0 · 10–3 м3
V2 = 5,0 л = 5,0 · 10–3 м3
Δp = –15 кПа = –1,5 · 104 Па
Решение: Так как температура и масса газа не изменяются, то его начальное и конечное состояния связаны законом Бойля–Мариотта, т. е. . С учётом того, что
, получим:
.
Откуда .
.
Ответ: .
![]()
Пример 3. В двух сосудах вместимостью V1 = 20 л и V2 = 30 л находятся химически не реагирующие идеальные газы, давления которых p1 = 1,0 МПа и p2 = 0,40 МПа соответственно. Определите давление газов в сосудах после того, как их соединили тонкой короткой трубкой. Температура газов до и после соединения сосудов одинаковая.
V1 = 20 л = 2,0 · 10-2 м3
V2 = 30 л = 3,0 · 10-2 м3
p1 = 1,0 МПа = 1,0 · 106 Па
p2 = 0,40 МПа = 4,0 · 105 Па
T = const
Решение: Давление смеси газов равно сумме парциальных давлений (закон Дальтона): . Найдём парциальное давление каждого газа после соединения сосудов. Так как температура и массы газов не изменяются, то начальное и конечное состояния каждого газа связаны законом Бойля–Мариотта, т. е.
,
.
Следовательно, парциальные давления газов после соединения сосудов: ,
. Тогда
.
Ответ: p = 0,64 МПа.
Упражнение 5
1. При изобарном увеличении температуры идеального газа, находящегося в герметично закрытом цилиндре, на ΔT = 60,0 К его объём увеличился в β = 1,21 раза. Определите начальную абсолютную температуру газа.
2. Изобразите графически процесс изобарного охлаждения определённой массы идеального газа в координатах (p, T); (V, T); (V, p).
3. Идеальный газ определённой массы сначала изобарно расширили, а затем изотермически сжали до первоначального объёма. Изобразите графически эти процессы в координатах (V, T); (p, V).
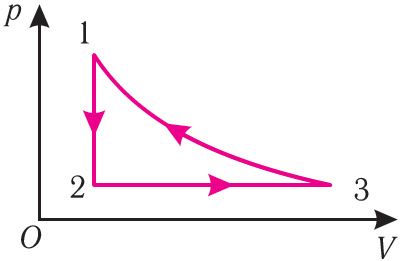
4. На рисунке 30 представлен график изменения состояния определённой массы идеального газа. (Переход 3 1 осуществляется при неизменной температуре.) Изобразите графически этот процесс в координатах (T, V) и (p, T).
5. При температуре t1 = –3,0 °С манометр на баллоне со сжатым кислородом показывал давление p1 = 1,8 · 106 Па, а при температуре t2 = 27 °С — давление p2 = 2,0 · 106 Па. Определите, была ли утечка газа из баллона.
![]()
6. В герметичном сосуде, заполненном воздухом (), лежит полый металлический шарик, диаметр которого d = 4,0 см, а масса m = 0,64 г. Определите минимальное значение давления воздуха, накачиваемого в сосуд, при котором бы шарик поднялся вверх, если температура t = 17 °С остаётся постоянной.
7. Идеальный газ, давление которого p1 = 4 · 105 Па, занимал объём V1 = 2 л. Сначала газ изотермически расширили до объёма V2 = 8 л, а затем изохорно нагрели, в результате чего его абсолютная температура увеличилась в α = 3 раза. Определите давление р3 газа в конце процесса, если при переходе из начального состояния в конечное масса газа оставалась неизменной.