*§ 8-1. Закон Авагадра. Адносная шчыльнасць газаў. Аб’ёмная доля газу ў сумесі
| Сайт: | Профильное обучение |
| Курс: | Хімія. 10 клас |
| Падручнік: | *§ 8-1. Закон Авагадра. Адносная шчыльнасць газаў. Аб’ёмная доля газу ў сумесі |
| Надрукаваны: | Гость |
| Дата: | Нядзеля 17 Жнівень 2025 |
Закон Авагадра. Адносная шчыльнасць газаў. Аб’ёмная доля газу ў сумесі
Як вам вядома, рэчывы могуць знаходзіцца ў цвёрдым, вадкім і газападобным стане. Малекулы вадкасці і цвёрдага рэчыва размяшчаюцца блізка адна да адной. Гэта магчыма дзякуючы таму, што малекулы прыцягваюцца адна да адной. Гэта значыць існуюць сілы, якія ўтрымліваюць малекулы вадкасці або цвёрдага рэчывы разам. З курса хіміі 8-га класа вы ведаеце, што гэтыя сілы называюцца сіламі міжмалекулярнага ўзаемадзеяння. Малекулы газаў знаходзяцца на значна большай адлегласці адна ад адной, чым у выпадку вадкасцей і цвёрдых рэчываў. На такой адлегласці малекулы практычна не ўзаемадзейнічаюць адна з адной. Таму, каб ператварыць вадкасць або цвёрдае рэчыва ў газ, неабходна пераадолець сілы міжмалекулярнага ўзаемадзеяння, аддаліўшы малекулы адна ад адной.
Пераход у газападобны стан ажыццяўляецца ў выніку награвання рэчываў, якія знаходзяцца ў цвёрдым або вадкім стане (кіпенне вадкасцей, узгонка цвёрдых рэчываў).
Так як адлегласць паміж малекуламі газаў значна большая за памеры саміх малекул, то аб’ём, які займае газ, — гэта, па сутнасці, аб’ём свабоднай прасторы паміж малекуламі газу, якія хаатычна рухаюцца. Велічыня гэтай прасторы вызначаецца ўмовамі, пры якіх знаходзіцца газ, гэта значыць тэмпературай і ціскам. Гэта велічыня прыкладна аднолькавая для ўсіх газаў. Пры гэтым аб’ём, які займаюць самі малекулы, можна не ўлічваць. Адсюль вынікае закон Авагадра — у роўных аб’ёмах розных газаў пры аднолькавых умовах змяшчаецца аднолькавы лік малекул.

Авагадра (1776—1856)
Цікава ведаць
З курса хіміі 8-га класа вы ўжо знаёмы з пастаяннай Авагадра, роўнай 6,02∙1023 моль–1, якая паказвае, колькі часціц змяшчаецца ў адным молі рэчыва. Гэта велічыня названа ў гонар выдатнага італьянскага вучонага Амедэа Авагадра, які ўнёс значны ўклад у развіццё малекулярнай фізікі, электрахіміі і іншых абласцей прыродазнаўства. На падставе даследавання суадносін аб’ёмаў газаў, якія рэагуюць і ўтвараюцца, такіх як вадарод і хлор, кісларод і азот, Авагадра ўпершыню выказаў здагадку, што малекулы азоту, кіслароду, вадароду і хлору складаюцца з двух атамаў. Гэта здагадка, якая спачатку доўга не знаходзіла разумення ў вучоных таго часу, пасля бліскуча пацвердзілася.
З закона Авагадра выцякаюць два асноўныя вывады.
Першы вывад. Адзін моль любога газу пры аднолькавых умовах займае аднолькавы аб’ём. Гэты аб’ём называецца малярным аб’ёмам газу (Vm) і вымяраецца ў дм3/моль. Малярны аб’ём газу роўны адносінам аб’ёму газу да яго колькасці:
![]() .
.
Велічыня Vm залежыць ад тэмпературы і ціску. Напрыклад, пры награванні газы расшыраюцца. Значыць, пры награванні павялічваецца малярны аб’ём газу. У сувязі з гэтым параўнанне характарыстык розных газавых сумясей неабходна ажыццяўляць пры аднолькавых умовах — тэмпературы і ціску. У якасці эталона такіх умоў прыняты нармальныя ўмовы (н. у.): тэмпература раставання лёду (0 °С або 273,15 K) і атмасферны ціск (101,3 кПа). Пры нармальных умовах Vm = 22,4 дм3/моль.
Такім чынам, з закона Авагадра вынікае, што 22,4 дм3 любога газу пры нармальных умовах змяшчаюць 6,02∙1023 малекул.
Другі вывад. Шчыльнасці газаў адносяцца паміж сабой як малярныя масы газаў.
Гэта відаць з наступных меркаванняў. Няхай маецца дзве порцыі розных газаў аднолькавага аб’ёму (аб’ёмы вымераны пры аднолькавых умовах). Разлічым іх шчыльнасці:
газ 1: ![]() ;
;
газ 2: ![]() .
.
Падзяліўшы шчыльнасць першага газу на шчыльнасць другога, атрымаем:
![]() .
.
Адносіны шчыльнасцей газаў, роўныя адносінам малярных мас, называюцца адноснай шчыльнасцю аднаго газу па другому (D). D — велічыня безпамерная.
Ведаючы D і малярную масу аднаго газу, лёгка знайсці малярную масу другога газу:
![]() ; M1 = M2 ∙ D.
; M1 = M2 ∙ D.
Прыклад 1. Адносная шчыльнасць газу па вадароду роўная 8. Вызначце малярную масу газу.
М(Х) = М(Н2) ∙ D = 2 ∙ 8 = 16 г/моль.
Газ з такой малярнай масай — метан СH4.
Прыклад 2. Адносная шчыльнасць некаторага газападобнага вуглевадароду па паветры роўная 2. Вызначце малярную масу вуглевадароду.
Сярэдняя малярная маса паветра роўная 29 г/моль;
М(Х) = М(паветра) ∙ D = 29 ∙ 2 = 58 г/моль.
Неабходна адзначыць, што газы з малярнай масай меншай за 29 лягчэйшыя за паветра, больш за 29 — цяжэйшыя.
У разліковых задачах могуць быць дадзены адносныя шчыльнасці невядомага газу па азоту, кіслароду і іншых газах. У гэтым выпадку для знаходжання малярнай масы невядомага газу неабходна памножыць адносную шчыльнасць на малярную масу адпаведна азоту (28 г/моль), кіслароду (32 г/моль) і г. д.
Закон Авагадра шырока прымяняецца ў хімічных разліках. Паколькі для газаў аб’ёмы прапарцыянальныя колькасцям (моль) рэчываў, то каэфіцыенты ва ўраўненні рэакцыі паміж газападобнымі рэчывамі, якія адлюстроўваюць колькасныя суадносіны рэагуючых рэчываў, прапарцыянальны аб’ёмам газаў, якія ўзаемадзейнічаюць. Відавочна, што аб’ёмы павінны быць вымераныя пры аднолькавых умовах.
Прыклад 3. Які аб’ём кіслароду спатрэбіцца для спальвання 2 дм3 прапану? Аб’ёмы вымераны пры н. у.
Ураўненне рэакцыі гарэння прапану:
С3Н8 + 5О2 ![]() 3СО2 + 4Н2О
3СО2 + 4Н2О
З закона Авагадра вынікае, што роўныя аб’ёмы розных газаў змяшчаюць аднолькавую колькасць (моль) рэчываў. Няхай аб’ём прапану роўны 1 дм3. Тады, згодна з прыведзеным ураўненнем, для спальвання 1 дм3 прапану спатрэбіцца 5 дм3 кіслароду. Такім чынам, для спальвання 2 дм3 прапану спатрэбіцца:
1 дм3 С3Н8 — 5 дм3 O2,
2 дм3 С3Н8 — 10 дм3 О2
Адказ: V(О2) = 10 дм3.
Сумесі газаў
Разгледзім дзве колбы аб’ёмам 0,5 дм3. Адна колба запоўнена азотам, а другая метанам. Ціск і тэмпература ў колбах аднолькавыя. Калі змяшаць змесціва гэтых колбаў, то атрыманая сумесь зойме пры такіх самых умовах аб’ём 1 дм3.
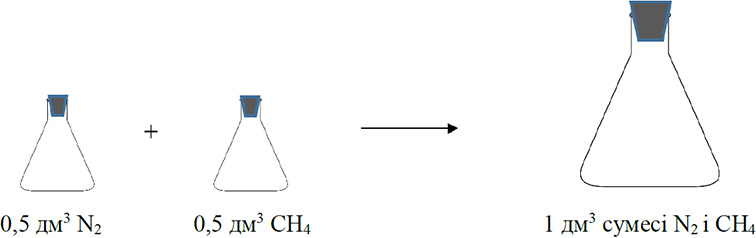
Састаў сумесі газаў часта выражаюць у аб’ёмных долях. Аб’ёмная доля газу абазначаецца грэчаскай літарай φ (фі) і роўна адносінам аб’ёму дадзенага газу да аб’ёму сумесі. Разлічым аб’ёмную долю азоту ў атрыманай вышэй сумесі газаў:
φ = ![]() = 0,5, або 50 %.
= 0,5, або 50 %.
Прыклад 4. У выніку прапускання 150 дм3 (н. у.) паветра праз лішак вапнавай вады выпала 0,201 г асадку. Знайдзіце аб’ёмную долю (%) вуглякіслага газу ў дадзеным узоры паветра.
Ураўненне рэакцыі ўзаемадзеяння вуглякіслага газу з вапнавай вадой:
СО2 + Са(ОН)2 = СаСО3![]() + Н2О
+ Н2О
Знойдзем колькасць (моль) карбанату кальцыю, які выпаў у асадак (M(CaCO3) = 100 г/моль):
n(СаСО3) = 0,201/100 = 0,00201 моль.
Па ўраўненню рэакцыі:
n(СаСО3) = n(СО2).
Разлічым аб’ёмную долю вуглякіслага газу ў паветры:
V(CO2) = 0,00201 ∙ 22,4 = 0,045 дм3;
φ(СО2) = 0,045/150 ∙ 0,0003, або 0,03 %.
Адказ: φ(СО2) = 0,03 %.
Прыклад 5. Аб’ём сумесі вадароду з хлорам складае 50 см3. Пасля ўзаемадзеяння газаў засталося 10 см3 хлору. Знайдзіце састаў зыходнай сумесі ў аб’ёмных долях. Усе аб’ёмы вымераны пры н. у.
Ураўненне рэакцыі ўзаемадзеяння вадароду з хлорам:
H2 + Cl2 ![]() 2HCl
2HCl
Паколькі пасля ўзаемадзеяння засталося 10 см3 хлору, то 40 см3 зыходнай сумесі прарэагавала. Хлор і вадарод рэагуюць паміж сабой у роўных аб’ёмных адносінах. Зыходзячы з гэтых меркаванняў, у рэакцыю ўступілі па 20 см3 хлору і вадароду. Паколькі засталося 10 см3 хлору, то ў першапачатковай сумесі было 20 см3 вадароду і 30 см3 хлору.
Разлічым аб’ёмныя долі газаў у зыходнай сумесі:
φ(H2) = 20/50 = 0,4, або 40 %;
φ(Cl2) = 30/50 = 0,6, або 60 %.
Адказ: φ(H2) = 40 %; φ(Cl2) = 60 %.
Згодна з законам Авагадра, у роўных аб’ёмах розных газаў пры аднолькавых умовах змяшчаецца аднолькавая колькасць малекул.
Адзін моль любога газу пры нармальных умовах (тэмпература таяння лёду, атмасферны ціск) займае аб’ём 22,4 дм3. Гэта велічыня называецца малярным аб’ёмам газу (Vm).
Шчыльнасці газаў, якія вымераны пры аднолькавых умовах, адносяцца паміж сабой як іх малярныя масы. Гэтыя адносіны называюцца адноснай шчыльнасцю аднаго газу па другому газу.
Газы, якія маюць малярную масу больш за 29 г/моль, цяжэшыя за паветра, а менш за 29 г/моль — лягчэйшыя за паветра.
Аб’ёмная доля газу ў сумесі роўна адносінам аб’ёму дадзенага газу да агульнага аб’ёму сумесі.
Пытанні і заданні
1. Сфармулюйце закон Авагадра. Чаму ён выконваецца для газападобных рэчываў і не выконваецца для рэчываў у цвёрдым або вадкім стане?
2. Што такое малярны аб’ём газу? Як ён змяняецца з павелічэннем тэмпературы і ціску?
3. Як вынікі эксперыментаў па вымярэнні аб’ёмаў газаў, якія ўдзельнічаюць у рэакцыях узаемадзеяння хлору з вадародам і азоту з кіслародам, дазволілі Авагадра прыйсці да высновы аб тым, што азот, кісларод, хлор і вадарод складаюцца з двухатамных малекул? Улічыце, што ў выніку ўзаемадзеяння азоту з кіслародам, што працякае толькі пры надзвычай высокай тэмпературы, утвараецца аксід азоту(II).
4. Адносная шчыльнасць па вадароду некаторага вуглевадароду роўная 15. Устанавіце малярную масу вуглевадароду і прывядзеце яго формулу.
5. У выніку выбуху сумесі, якая складалася з 1 дм3 невядомага газу і 2 дм3 кіслароду (зыходныя рэчывы прарэагавалі цалкам), утварылася 2 дм3 вуглякіслага газу і 1 дм3 азоту. Усе аб’ёмы вымераны пры аднолькавых умовах. Устанавіце формулу невядомага газу.
(Адказ: C2N2.)